Тэрмадынамічная бэта

Шкала пераўтварэння тэмпературы/халоднасці СІ: Тэмпературы па шкале Кельвіна паказаны сінім (шкала Цэльсія — зялёным, шкала Фарэнгейта — чырвоным), значэнні халоднасці ў гігабайтах на нанаджоўль паказаны чорным. Бясконцая тэмпература (нулявая халоднасць) паказана ўверсе дыяграмы; станоўчыя значэнні халоднасці/тэмпературы — справа, адмоўныя — злева.

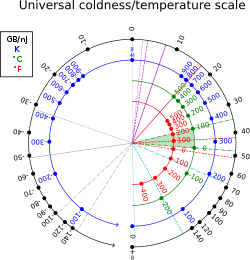
У статыстычнай тэрмадынаміцы тэрмадынамічная бэта, таксама вядомая як халоднасць, з'яўляецца велічынёй, адваротнай тэрмадынамічнай тэмпературы сістэмы:$$\beta ={\frac {1}{k_{\rm {B}}T}}$$ (дзе T — тэмпература, а k_B — пастаянная Больцмана).

Тэрмадынамічная бэта мае размернасць, адваротную энергіі (у адзінках СІ, адваротны джоўль, $[\beta ]={\textrm {J}}^{-1}$). У нетэрмальных адзінках яе таксама можна вымяраць у байтах на джоўль або, што зручней, у гігабайтах на нанаджоўль; 1 K⁻¹ эквівалентны прыкладна 13 062 гігабайтам на нанаджоўль; пры пакаёвай тэмпературы: T = 300 K, β ≈ 44ГБ/нДж ≈ 39эВ⁻¹ ≈ 2.4×10²⁰Дж⁻¹. Каэфіцыент пераўтварэння: 1 ГБ/нДж = $8\ln 2\times 10^{18}$ Дж⁻¹.

Апісанне

Тэрмадынамічная бэта, па сутнасці, з'яўляецца звязуючым звяном паміж тэорыяй інфармацыі і статыстычнай механікай у інтэрпрэтацыі фізічнай сістэмы праз яе энтрапію і тэрмадынамікай, звязанай з яе энергіяй. Яна выражае рэакцыю энтрапіі на павелічэнне энергіі. Калі да сістэмы дадаецца невялікая колькасць энергіі, то β апісвае ступень рандомізацыі сістэмы.

Праз статыстычнае вызначэнне тэмпературы як функцыі энтрапіі, функцыю халоднасці можна вылічыць у мікракананічным ансамблі па формуле

$\beta ={\frac {1}{k_{\rm {B}}T}}\,={\frac {1}{k_{\rm {B}}}}\left({\frac {\partial S}{\partial E}}\right)_{V,N}$

(г.зн. частковая вытворная энтрапіі S па энергіі E пры пастаянным аб'ёме V і ліку часціц N).

Перавагі

Хоць β цалкам эквівалентная тэмпературы па канцэптуальным змесце, яна звычайна лічыцца больш фундаментальнай велічынёй, чым тэмпература, з-за з'явы адмоўнай тэмпературы, пры якой β бесперапынная пры пераходзе праз нуль, у той час як T мае сінгулярнасць.

Акрамя таго, у β ёсць перавага ў тым, што яе прычынна-выніковую сувязь лягчэй зразумець: калі да сістэмы дадаецца невялікая колькасць цяпла, β прадстаўляе павелічэнне энтрапіі, падзеленае на павелічэнне цяпла. Тэмпературу складана інтэрпрэтаваць у тым жа сэнсе, бо немагчыма "дадаць энтрапію" да сістэмы інакш, як ускосна, змяняючы іншыя велічыні, такія як тэмпература, аб'ём або лік часціц.

Статыстычная інтэрпрэтацыя

З пункту гледжання статыстыкі, β — гэта лікавая велічыня, якая звязвае дзве макраскапічныя сістэмы ў раўнавазе. Дакладная фармулёўка наступная. Разгледзім дзве сістэмы, 1 і 2, якія знаходзяцца ў цеплавым кантакце, з адпаведнымі энергіямі E₁ і E₂. Выкажам здагадку, што E₁ + E₂ = некаторая пастаянная E. Колькасць мікрастанаў кожнай сістэмы абазначым Ω₁ і Ω₂. У рамках нашых здагадак Ω_i залежыць толькі ад E_i. Мы таксама выкажам здагадку, што любое мікрастан сістэмы 1, сумяшчальнае з E₁, можа суіснаваць з любым мікрастанам сістэмы 2, сумяшчальным з E₂. Такім чынам, колькасць мікрастанаў для аб'яднанай сістэмы роўна

$\Omega =\Omega _{1}(E_{1})\Omega _{2}(E_{2})=\Omega _{1}(E_{1})\Omega _{2}(E-E_{1}).\,$

Мы выведзем β з асноўнага пастулата статыстычнай механікі:

Калі аб'яднаная сістэма дасягае раўнавагі, лік Ω максімізуецца.

(Іншымі словамі, сістэма натуральным чынам імкнецца да максімальнага ліку мікрастанаў.) Такім чынам, у раўнавазе:

${\frac {d}{dE_{1}}}\Omega =\Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})+\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})\cdot {\frac {dE_{2}}{dE_{1}}}=0.$

Але E₁ + E₂ = E мае на ўвазе

${\frac {dE_{2}}{dE_{1}}}=-1.$

Так што

$\Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})-\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})=0$

г.зн.

${\frac {d}{dE_{1}}}\ln \Omega _{1}={\frac {d}{dE_{2}}}\ln \Omega _{2}\quad {\mbox{у раўнавазе.}}$

Вышэйпрыведзенае суадносіны матывуе вызначэнне β:

$\beta ={\frac {d\ln \Omega }{dE}}.$

Сувязь статыстычнай і тэрмадынамічнай інтэрпрэтацый

Калі дзве сістэмы знаходзяцца ў раўнавазе, яны маюць аднолькавую тэрмадынамічную тэмпературу T. Таму інтуітыўна можна чакаць, што β (вызначаная праз мікрастаны) нейкім чынам звязана з T. Гэтая сувязь забяспечваецца асноўным пастулатам Больцмана, запісаным як

$S=k_{\rm {B}}\ln \Omega ,$

дзе k_B — пастаянная Больцмана, S — класічная тэрмадынамічная энтрапія, а Ω — лік мікрастанаў. Такім чынам,

$d\ln \Omega ={\frac {1}{k_{\rm {B}}}}dS.$

Падстаўляючы ў вызначэнне β са статыстычнага вызначэння вышэй, атрымліваем

$\beta ={\frac {1}{k_{\rm {B}}}}{\frac {dS}{dE}}.$

Параўноўваючы з тэрмадынамічнай формулай

${\frac {dS}{dE}}={\frac {1}{T}},$

маем

$\beta ={\frac {1}{k_{\rm {B}}T}}={\frac {1}{\tau }}$

дзе $\tau$ называецца фундаментальнай тэмпературай сістэмы і мае размернасць энергіі.

Гісторыя

Тэрмадынамічная бэта была першапачаткова ўведзена ў 1971 годзе (як Kältefunktion «функцыя халоднасці») Інга Мюлерам, адным з прыхільнікаў школы думкі рацыянальнай тэрмадынамікі, на аснове больш ранніх прапаноў аб функцыі «адваротнай тэмпературы».

Гл. таксама

Размеркаванне Больцмана

Кананічны ансамбль

Мадэль Ізінга