전기역학 테더

70mm 카메라로 촬영된 테더 위성 시스템 배치 장면의 근접 촬영.

전기역학 테더(영어: Electrodynamic tether, EDT)는 테더 위성에서 배치되는 것과 같은 긴 전도성 철사로, 운동 에너지를 전기 에너지로 변환하여 발전기로 작동하거나, 전기 에너지를 운동 에너지로 변환하여 전동기로 작동하는 전자기학 원리에 따라 작동할 수 있다. 전기 전위는 행성의 자기장을 통과하는 전도성 테더의 움직임에 의해 생성된다.

여러 임무에서 우주에서의 전기역학 테더를 시연했는데, 가장 주목할 만한 것은 TSS-1, TSS-1R, 그리고 플라스마 모터 발전기 (PMG) 실험이다.

테더 추진

테더 추진 시스템의 일부로, 우주선은 길고 강력한 도체(모든 테더가 전도성은 아님)를 사용하여 우주선의 궤도를 변경할 수 있다. 이는 우주 여행을 훨씬 더 저렴하게 만들 잠재력이 있다. 직류가 테더에 가해지면, 자기장에 대해 로런츠 힘을 가하고, 테더는 차량에 힘을 가한다. 이는 궤도를 도는 우주선을 가속하거나 감속하는 데 사용될 수 있다.

2012년에 스타 기술 연구(Star Technology and Research)는 우주 쓰레기 제거를 위한 테더 추진 시스템을 검증하기 위해 190만 달러의 계약을 수주했다.

ED 테더의 용도

수년에 걸쳐 전기역학 테더의 수많은 응용 분야가 산업, 정부 및 과학 탐사에서 잠재적으로 사용될 수 있는 것으로 확인되었다. 아래 표는 지금까지 제안된 잠재적 응용 분야 중 일부를 요약한 것이다. 이러한 응용 분야 중 일부는 일반적인 개념인 반면, 다른 일부는 잘 정의된 시스템이다. 이들 개념 중 다수는 다른 분야와 중복되지만, 이 표의 목적을 위해 가장 적절한 제목 아래에 배치되었다. 표에 언급된 모든 응용 분야는 테더 핸드북(Tethers Handbook)에 자세히 설명되어 있다. 테더가 지닌 세 가지 근본적인 개념은 중력 기울기, 운동량 교환 및 전기역학이다. 잠재적 테더 응용 분야는 아래에서 확인할 수 있다.

전기역학
전기역학 발전	전기역학 추진력 생성
ULF/ELF/VLF 통신 안테나	방사선대 치료
우주 정거장
미세 중력 실험실	우주 정거장에서 셔틀 궤도 이탈
테더 우주 수송선(STV) 발사	가변/저 중력 실험실
자세 안정화 및 제어	ISS 재부스트
운송
일반화된 운동량 회수된 사용 후 로켓	궤도 수정을 위한 내부 힘
궤도선에서 위성 부스트	테더 보조 운송 시스템(TATS)
쇠퇴하는 위성의 테더 재부스트	궤도선에서 상부 단계 부스트

ISS 재부스트

EDT는 ISS 궤도를 유지하고 화학 추진제 재부스트 비용을 절감하기 위해 제안되었다. 이는 미세 중력 조건의 품질과 지속 시간을 향상시킬 수 있다.

전기역학 테더 기본 원리

EDT 개념도

전기역학 테더에 사용될 금속 도체의 선택은 다양한 요인에 의해 결정된다. 주요 요인으로는 일반적으로 높은 도전율과 낮은 밀도가 포함된다. 이차적인 요인은 적용 분야에 따라 비용, 강도, 녹는점이 포함된다.

테더 요소가 자기장에 대해 상대적으로 움직일 때 기전력 (EMF)이 발생한다. 이 힘은 패러데이 전자기 유도 법칙에 의해 다음과 같이 주어진다.

$V_{\mathrm {emf} }=\int _{0}^{L}\left({\vec {v}}_{\mathrm {orb} }\times {\vec {B}}\right)d{\vec {L}}.$

일반성을 잃지 않고, 테더 시스템은 지구 궤도에 있으며 지구 자기장에 대해 상대적으로 움직인다고 가정한다. 마찬가지로, 전류가 테더 요소에 흐르면 로런츠 힘 방정식에 따라 힘이 생성될 수 있다.

${\vec {F}}=\int _{0}^{L}I(L)\,d{\vec {L}}\times {\vec {B}}.$

자체 구동 모드(궤도 이탈 모드)에서 이 EMF는 테더 시스템이 테더와 다른 전기 부하(예: 저항기, 배터리)를 통해 전류를 구동하고, 방출 끝에서 전자를 방출하거나, 반대쪽에서 전자를 수집하는 데 사용될 수 있다. 부스트 모드에서는 온보드 전원 공급 장치가 이 운동 EMF를 극복하여 전류를 반대 방향으로 구동해야 하며, 아래 그림에서 볼 수 있듯이 반대 방향으로 힘을 생성하여 시스템을 부스트한다.

예를 들어, 위 그림에 나타난 NASA 추진성 소형 배치 시스템 (ProSEDS) 임무를 보자. 고도 300km에서 북-남 방향의 지구 자기장은 약 0.18–0.32 가우스이며, 약 40°의 경사까지 상승하며, 국부 플라스마에 대한 궤도 속도는 약 7500m/s이다. 이로 인해 5km 길이의 테더를 따라 35–250V/km의 V_emf 범위가 발생한다. 이 EMF는 베어 테더에 걸쳐 전위차를 결정하며, 이는 전자가 수집되거나/또는 반발되는 지점을 제어한다. 여기서 ProSEDS 감속 테더 시스템은 베어 테더의 양전하를 띠는 고고도 섹션으로 전자 수집을 가능하게 하고, 저고도 끝에서 전리층으로 되돌아가도록 구성된다. 지구 자기장 존재 하에 테더 길이를 통한 이러한 전자 흐름은 위 방정식에 의해 주어진 것처럼 시스템의 궤도 이탈을 돕는 항력 추력을 생성하는 힘을 생성한다. 부스트 모드는 궤도 이탈 모드와 유사하지만, 고전압 전원 공급 장치(HVPS)가 테더와 더 높은 양전위 끝 사이에 테더 시스템과 직렬로 삽입된다는 점이 다르다. 전원 공급 장치 전압은 EMF보다 크고 극성이 반대여야 한다. 이는 전류를 반대 방향으로 구동하여, 결과적으로 고고도 끝은 음전하를 띠고, 저고도 끝은 양전하를 띠게 한다(지구 주위를 동쪽에서 서쪽으로 표준 궤도를 가정).

감속 현상을 더 강조하기 위해, 절연되지 않은 베어 테더 시스템(모두 노출)의 개략도가 아래 그림에 나와 있다.

발전기(감속) 모드에서 작동하는 베어 테더의 전류 및 전압 플롯 대 거리

다이어그램의 상단, 지점 A는 전자 수집 끝을 나타낸다. 테더의 하단, 지점 C는 전자 방출 끝이다. 마찬가지로, $V_{\mathrm {anode} }$와 $V_{\mathrm {cathode} }$는 각각의 테더 끝에서 플라스마까지의 전위차를 나타내며, $V-V_{p}$는 플라스마에 대한 테더의 모든 지점에서의 전위이다. 마지막으로, 지점 B는 테더의 전위가 플라스마와 같은 지점이다. 지점 B의 위치는 키르히호프의 전압 법칙 (KVL)과

$V_{\mathrm {anode} }+\int _{A}^{C}I(y)\,dR_{t}+R_{\mathrm {load} }I_{C}+V_{\mathrm {emit} }+V_{\mathrm {cathode} }=V_{\mathrm {emf} }$

키르히호프의 전류 법칙 (KCL)

$I_{AB}=I_{BC}+I_{C}$

의 해에 의해 결정되는 테더의 평형 상태에 따라 달라진다. 여기서 $I_{AB}$, $I_{BC}$ 및 $I_{C}$는 각각 지점 A에서 B까지의 전류 이득, 지점 B에서 C까지의 손실 전류 및 지점 C에서의 손실 전류를 나타낸다.

테더의 노출된 길이를 따라 전류가 지속적으로 변하기 때문에, 전선의 저항적 특성으로 인한 전위 손실은 $\textstyle \int _{A}^{C}I(y)\,dR_{t}$로 표현된다. 테더의 무한소 단면을 따라 저항 $dR_{t}$에 그 단면을 통과하는 전류 $I(y)$를 곱한 값이 저항적 전위 손실이다.

시스템에 대한 KVL 및 KCL을 평가한 후, 결과는 위 그림에서 볼 수 있듯이 테더를 따라 전류 및 전위 프로파일을 제공한다. 이 다이어그램은 테더의 A 지점에서 B 지점까지 양의 전위 편향이 있어 수집된 전류를 증가시킨다는 것을 보여준다. 그 지점 아래에서는 $V-V_{p}$가 음수가 되고 이온 전류 수집이 시작된다. 동등한 양의 이온 전류(주어진 면적에 대해)를 수집하는 데 훨씬 더 큰 전위차가 필요하기 때문에, 테더의 총 전류는 더 적은 양으로 감소한다. 그런 다음 C 지점에서 시스템에 남아있는 전류는 저항 부하($R_{\mathrm {load} }$)를 통해 흐르고, 전자 방출 장치($V_{\mathrm {emit} }$)에서 방출되며, 마지막으로 플라스마 시스($V_{\mathrm {cathode} }$)를 가로지른다. KVL 전압 루프는 전리층에서 닫히며, 여기서 전위차는 사실상 0이다.

베어 EDT의 특성상 테더 전체를 노출시키는 것은 선택 사항이 아닌 경우가 많다. 시스템의 추진 능력을 최대화하려면 베어 테더의 상당 부분을 절연해야 한다. 이 절연량은 플라스마 밀도, 테더 길이와 너비, 궤도 속도, 지구 자기장 밀도 등 여러 효과에 따라 달라진다.

발전기로서의 테더

 이 부분의 본문은 발전기입니다.

우주 객체, 즉 지구 궤도를 도는 위성 또는 다른 자연적이거나 인공적인 우주 객체가 테더 시스템에 물리적으로 연결된다. 테더 시스템은 우주 객체에서 위로 뻗어 있는 베어 세그먼트를 가진 전도성 테더를 배치하는 배치기로 구성된다. 테더의 양전하를 띤 양극 끝은 우주 객체가 지구 자기장을 가로질러 움직이는 방향으로 이동함에 따라 전리층에서 전자를 수집한다. 이 전자들은 테더의 전도성 구조를 통해 전원 시스템 인터페이스로 흐르고, 여기서 연결된 부하(표시되지 않음)에 전력을 공급한다. 전자들은 그 다음 음전하를 띤 음극으로 흘러가고, 여기서 전자들은 우주 플라스마로 방출되어 전기 회로를 완성한다. (출처: 미국 특허 6,116,544, "Electrodynamic Tether And Method of Use".)

전기역학 테더는 물체에 부착되며, 테더는 물체와 자기장을 가진 행성 사이의 국부 수직선에 대해 일정한 각도로 향하게 된다. 테더의 먼 끝은 노출된 채로 두어 전기 접촉을 전리층과 할 수 있다. 테더가 행성의 자기장과 교차할 때 전류를 생성하여 궤도 물체의 운동 에너지 일부를 전기 에너지로 변환한다. 기능적으로, 전자들은 우주 플라스마에서 전도성 테더로 흐르고, 제어 장치의 저항 부하를 통과하며, 전자 방출기에 의해 자유 전자로 우주 플라스마로 방출된다. 이 과정의 결과로, 전기역학적 힘이 테더와 부착된 물체에 작용하여 그들의 궤도 운동을 늦춘다. 느슨한 의미에서 이 과정은 일반적인 풍차와 유사하다고 볼 수 있다. 저항성 매개체(공기 또는 이 경우 자기권)의 항력이 상대 운동(바람 또는 위성의 운동량)의 운동 에너지를 전기로 변환하는 데 사용된다. 원칙적으로 소형 고전류 테더 발전기가 가능하며, 기본적인 하드웨어로 수십, 수백, 수천 킬로와트가 달성 가능해 보인다.

 다이너모 문서에 이 부분의 추가 정보가 있습니다.

전압 및 전류

NASA는 우주에서 플라스마 모터 발전기(PMG) 테더를 이용한 여러 실험을 수행했다. 초기 실험에서는 500미터 길이의 전도성 테더를 사용했다. 1996년 NASA는 20,000미터 길이의 전도성 테더를 이용한 실험을 진행했다. 이 테스트 동안 테더가 완전히 전개되었을 때, 궤도를 도는 테더는 3,500볼트의 전위를 생성했다. 이 전도성 단일 라인 테더는 전개 5시간 후에 절단되었다. 이 고장은 전도성 테더가 지구 자기장을 통과하며 움직일 때 발생하는 전기 아크에 의해 발생한 것으로 추정된다.

테더가 지구의 자기장(B)에 직각으로 속도(v)로 움직일 때, 테더의 기준 프레임에서 전기장이 관찰된다. 이는 다음과 같이 표현될 수 있다.

E = v * B = vB

전기장(E)의 방향은 테더의 속도(v)와 자기장(B) 모두에 직각이다. 테더가 도체인 경우, 전기장은 테더를 따라 전하의 변위를 초래한다. 이 방정식에 사용된 속도는 테더의 궤도 속도이다. 지구 또는 지구 핵의 회전 속도는 관련이 없다. 이와 관련하여 단극 발전기도 참조하라.

 패러데이 전자기 유도 법칙 문서에 이 부분의 추가 정보가 있습니다.

도체 양단의 전압

길이 L인 긴 전도성 철사의 경우, 철사에 전기장 E가 생성된다. 이는 철사의 반대쪽 끝 사이에 전압 V를 생성한다. 이는 다음과 같이 표현할 수 있다.

$V=\mathbf {E} \cdot \mathbf {L} =EL\cos \tau =vBL\cos \tau$

여기서 각 τ는 테더의 길이 벡터(L)와 전기장 벡터(E) 사이의 각도이며, 이는 평면 내에서 속도 벡터(v)에 직각인 수직 방향으로 가정되고 자기장 벡터(B)는 평면 밖으로 향한다.

도체 내 전류

전기역학 테더는 일종의 "개방 시스템"으로 설명될 수 있다. 전기역학 테더 회로는 단순히 다른 전선을 사용하여 완성될 수 없는데, 이는 다른 테더가 유사한 전압을 발생시키기 때문이다. 다행히도 지구의 자기권은 "비어있지" 않으며, 지구 근처 지역(특히 지구 대기권 근처)에는 태양 복사 또는 기타 복사 에너지에 의해 부분적으로 이온화된 고도로 전도성 있는 플라스마가 존재한다. 전자 및 이온 밀도는 위치, 고도, 계절, 태양 흑점 주기, 오염 수준 등 다양한 요인에 따라 달라진다. 양전하를 띤 베어 도체가 플라스마에서 자유 전자를 쉽게 제거할 수 있다는 것이 알려져 있다. 따라서 전기 회로를 완성하려면 테더의 상부, 양전하를 띤 끝에 충분히 넓은 면적의 절연되지 않은 도체가 필요하며, 이를 통해 테더를 통해 전류가 흐를 수 있게 된다.

그러나 테더의 반대쪽(음극) 끝이 자유 전자를 방출하거나 플라스마에서 양이온을 수집하는 것은 더 어렵다. 테더의 한쪽 끝에 매우 넓은 수집 영역을 사용하면 충분한 이온을 수집하여 플라스마를 통해 상당한 전류를 흐르게 할 수 있다. 이는 셔틀 궤도선의 TSS-1R 임무 동안 입증되었는데, 셔틀 자체가 대형 플라스마 접촉기로 사용되어 1암페어 이상의 전류를 공급했다. 개선된 방법으로는 열전자 방출 음극, 플라스마 음극, 플라스마 접촉기 또는 전계 전자 방출 장치와 같은 전자 방출기를 만드는 것이 포함된다. 테더의 양쪽 끝이 주변 플라스마에 "개방"되어 있으므로, 전자는 테더의 한쪽 끝에서 흘러나가고 해당 전자 흐름이 다른 쪽 끝으로 들어올 수 있다. 이러한 방식으로 테더 내에서 전자기적으로 유도된 전압은 주변 우주 환경을 통해 전류가 흐르게 하여, 언뜻 보기에는 개방 회로로 보이는 것을 통해 전기 회로를 완성할 수 있다.

테더 전류

테더를 통해 흐르는 전류(I)의 양은 다양한 요인에 따라 달라진다. 이 중 하나는 회로의 총 저항(R)이다. 회로의 저항은 세 가지 구성 요소로 구성된다.

1. 플라스마의 유효 저항
2. 테더의 저항
3. 제어 가변 저항

또한, 기생 부하가 필요하다. 전류 부하는 배터리와 같은 예비 전원을 충전하는 충전 장치의 형태를 취할 수 있다. 배터리는 차례로 전력 및 통신 회로를 제어하고, 테더의 음극 끝에 있는 전자 방출 장치를 구동하는 데 사용된다. 따라서 테더는 배치 및 시동 절차에 필요한 초기 배터리 충전 외에는 완전히 자체 동력을 사용할 수 있다.

충전 배터리 부하는 전력을 흡수하지만(즉시 열을 발산하는 대신) 나중에 사용하기 위해 저장하는 저항으로 볼 수 있다. 이는 "제어 저항"의 일부로 포함된다. 충전 배터리 부하는 "기본 저항"으로 취급되지 않는다. 충전 회로는 언제든지 끌 수 있기 때문이다. 꺼져 있을 때는 배터리에 저장된 전력을 사용하여 중단 없이 작업을 계속할 수 있다.

 분산 요소 모델 문서에 이 부분의 추가 정보가 있습니다.

EDT 시스템의 전류 수집/방출: 이론과 기술

주변 플라스마로부터 전하 및 이온 전류를 수집하고 방출하는 것을 이해하는 것은 대부분의 EDT 시스템에 매우 중요하다. EDT 시스템의 노출된 모든 전도성 부분은 우주선 본체의 전기 전위에 따라 주변 플라스마에 대해 수동적으로('수동적' 및 '능동적' 방출은 원하는 효과를 얻기 위해 미리 저장된 에너지를 사용하는 것을 의미함) 전자 또는 이온 전류를 수집할 수 있다. 또한, 전도성 본체의 기하학적 구조는 시스(sheath)의 크기와 전체 수집 능력에 중요한 역할을 한다. 결과적으로, 다양한 수집 기술에 대한 여러 이론이 존재한다.

EDT 시스템에서 전자 및 이온 수집을 제어하는 주요 수동적 과정은 열 전류 수집, 이온 램 수집 효과, 전자 광전 방출, 그리고 가능하게는 2차 전자 및 이온 방출이다. 또한, 얇은 베어 테더를 따라 흐르는 전류 수집은 궤도 운동 제한(OML) 이론과 플라스마 디바이 길이에 대한 물리적 크기에 따라 이 모델에서 파생된 이론적 유도를 사용하여 설명된다. 이러한 과정은 전체 시스템의 노출된 모든 전도성 물질을 따라 발생한다. 환경 및 궤도 매개변수는 수집된 전류량에 상당한 영향을 미칠 수 있다. 몇 가지 중요한 매개변수에는 플라스마 밀도, 전자 및 이온 온도, 이온 분자량, 자기장 강도 및 주변 플라스마에 대한 궤도 속도가 포함된다.

또한 EDT 시스템에는 능동적인 수집 및 방출 기술이 포함된다. 이는 중공 음극 플라스마 접촉기, 열전자 방출 음극 및 전계 방출 배열과 같은 장치를 통해 발생한다. 이러한 각 구조의 물리적 설계와 전류 방출 능력은 철저히 논의된다.

베어 전도성 테더

노출된 전도성 테더로의 전류 수집 개념은 산마르틴과 마르티네스-산체스에 의해 처음으로 정립되었다. 그들은 가장 면적 효율적인 전류 수집 원통형 표면은 유효 반경이 약 1 디바이 길이 미만인 표면이며, 여기서 전류 수집 물리학은 충돌 없는 플라스마에서 궤도 운동 제한(OML)으로 알려져 있다고 언급한다. 베어 전도성 테더의 유효 반경이 이 지점을 초과하면 OML 이론에 비해 수집 효율이 예측 가능하게 감소한다. 이 이론(비흐름 플라스마에 대해 유도됨) 외에도 우주에서의 전류 수집은 흐르는 플라스마에서 발생하며, 이는 또 다른 수집 효과를 유도한다. 이러한 문제는 아래에서 더 자세히 다루어진다.

궤도 운동 제한(OML) 이론

전자 디바이 길이는 플라스마에서 특성 차폐 거리로 정의되며, 다음 방정식으로 설명된다.

$\lambda _{\mathrm {De} }\cong {\sqrt {\frac {\varepsilon _{0}T_{e}}{qn_{0}}}}.$

전도성 물체로 인해 플라스마에서 발생하는 모든 전기장이 1/e로 감소하는 이 거리를 계산할 수 있다. OML 이론은 전자 디바이 길이가 물체의 크기와 같거나 크고 플라스마가 흐르지 않는다고 가정하여 정의된다. OML 체제는 시스가 충분히 두꺼워져서 입자 수집에서 궤도 효과가 중요해질 때 발생한다. 이 이론은 입자 에너지와 각운동량을 설명하고 보존한다. 결과적으로, 두꺼운 시스의 표면에 입사하는 모든 입자가 수집되는 것은 아니다. 주변 플라스마에 대한 수집 구조의 전압과 주변 플라스마 밀도 및 온도가 시스의 크기를 결정한다. 이 가속(또는 감속) 전압은 입사 입자의 에너지 및 운동량과 결합되어 플라스마 시스를 가로질러 수집되는 전류량을 결정한다.

궤도 운동 제한(OML) 체제는 실린더 반경이 충분히 작아서 수집되는 모든 입자 궤적이 실린더 표면에서 종료되고 배경 플라스마에 연결될 때 (즉, 다른 지점에서는 연결되지 않음) 달성된다. 준중성 충돌 없는 플라스마에서 입자 궤적을 따라 분포 함수가 보존되므로, 모든 "도착 방향"이 채워지는 것은 단위 면적당 수집되는 전류의 상한선에 해당한다 (총 전류는 아님).

EDT 시스템에서 주어진 테더 질량에 대한 최상의 성능은 전형적인 전리층 주변 조건(고도 200~2000km 범위의 전형적인 전리층 조건에서 T_e는 0.1eV~0.35eV, n_e는 10^10 m^-3~10^12 m^-3)에 대한 전자 디바이 길이보다 작은 테더 직경을 선택하는 것이다. 따라서 이는 OML 체제 내에 있다. 이 차원 밖의 테더 형상은 다루어졌다. OML 수집은 다양한 샘플 테더 형상 및 크기에 대한 전류 수집 결과를 비교할 때 기준선으로 사용될 것이다.

1962년에 제럴드 해리스 로젠은 현재 먼지 대전의 OML 이론으로 알려진 방정식을 유도했다. 아이오와 대학교의 로버트 멀리노에 따르면 로젠은 다른 누구보다 30년 전에 그 방정식에 도달한 것으로 보인다.

흐르지 않는 플라스마에서의 OML 이론의 편차

다양한 실용적인 이유로, 노출된 EDT로의 전류 수집이 항상 OML 수집 이론의 가정을 만족시키는 것은 아니다. 이러한 조건에서 예측된 성능이 이론과 어떻게 다른지 이해하는 것이 중요하다. EDT에 대해 일반적으로 제안되는 두 가지 형상은 원통형 철사와 평평한 테이프를 사용하는 것이다. 원통형 테더가 반경에서 하나의 디바이 길이보다 작다면 OML 이론에 따라 수집될 것이다. 그러나 너비가 이 거리를 초과하면 수집은 이 이론에서 점점 더 벗어난다. 테더 형상이 평평한 테이프라면, 정규화된 테이프 너비를 동등한 원통 반경으로 변환하는 근사치를 사용할 수 있다. 이것은 산마르틴과 에스테스에 의해 처음 시도되었고 최근에는 초이니에르 외에 의해 2차원 운동학적 플라스마 솔버(KiPS 2-D)를 사용하여 수행되었다.

흐르는 플라스마 효과

현재, 베어 테더에 대한 플라스마 흐름의 효과를 설명하는 폐쇄형 해법은 없다. 그러나 초이니에르 외에 의해 KiPS-2D를 사용하여 수치 시뮬레이션이 최근 개발되었으며, 이는 높은 바이어스 전위에서 간단한 형상에 대한 흐름 사례를 시뮬레이션할 수 있다. EDT에 적용되는 이 흐르는 플라스마 분석은 논의되었다. 이 현상은 현재 최근 연구를 통해 조사 중이며, 완전히 이해되지 않았다.

종단체 수집

이 섹션에서는 ED 테더의 끝에 적용될 대형 전도성 물체에 대한 수동 전류 수집을 설명하는 플라스마 물리학 이론을 논의한다. 시스의 크기가 수집하는 물체의 반경보다 훨씬 작을 때, 테더의 전위와 주변 플라스마의 전위(V – Vp) 차이의 극성에 따라 플라스마 시스로 들어오는 모든 전자나 이온이 전도성 물체에 의해 수집된다고 가정한다. 흐르지 않는 플라스마를 포함하는 이 '얇은 시스' 이론이 논의된 후, 흐르는 플라스마에 대한 이 이론의 수정 사항이 제시된다. 다른 전류 수집 메커니즘이 이어서 논의될 것이다. 제시된 모든 이론은 EDT 임무 중 발생하는 모든 조건을 설명하기 위한 전류 수집 모델을 개발하는 데 사용된다.

수동 수집 이론

자기장이 없는 흐르지 않는 준중성 플라스마에서 구형 전도성 물체는 모든 방향에서 동일하게 전하를 수집한다고 가정할 수 있다. 말단체에서의 전자 및 이온 수집은 Ithi 및 Ithe로 주어지는 열 수집 과정에 의해 지배된다.

흐르는 플라스마 전자 수집 모드

전류 수집에 대한 보다 현실적인 모델을 개발하는 다음 단계는 자기장 효과와 플라스마 흐름 효과를 포함하는 것이다. 충돌 없는 플라스마를 가정하면, 전자와 이온은 자기 미러링 힘과 기울기-곡률 드리프트로 인해 지구 주변의 극 사이를 이동하면서 자기장 선 주위를 회전한다. 그들은 질량, 자기장 강도, 에너지에 따라 특정 반경과 주파수로 회전한다. 이러한 요인들은 전류 수집 모델에서 고려되어야 한다.

파일:Fig28 plasma collection.PNG

TSS 위성 근접 환경에서 관찰된 복잡한 물리적 효과 및 특성의 복합 개략도

흐르는 플라스마 이온 수집 모델

전도성 물체가 플라스마에 대해 음전하를 띠고 이온 열 속도 이상으로 이동할 때, 추가적인 수집 메커니즘이 작동한다. 일반적인 저궤도(LEO)의 경우, 200km에서 2000km 사이에서, 관성 기준 프레임에서 속도는 원형 궤도의 경우 7.8km/s에서 6.9km/s까지 다양하며, 대기 분자량은 각각 25.0 amu (O+, O2+, & NO+)에서 1.2 amu (대부분 H+)까지 다양하다. 전자 및 이온 온도가 ~0.1 eV에서 0.35 eV 사이라고 가정하면, 결과적인 이온 속도는 200km에서 2000km 고도까지 각각 875m/s에서 4.0km/s까지 다양하다. 전자는 LEO 전역에서 약 188km/s로 이동한다. 이는 궤도를 도는 물체가 이온보다 빠르고 전자보다 느리게, 즉 중간음속으로 이동한다는 것을 의미한다. 이는 궤도를 도는 물체가 플라스마의 주변 이온을 "충돌"하여 궤도를 도는 물체의 기준 프레임에서 빔과 같은 효과를 생성하는 독특한 현상을 초래한다.

다공성 종단체

다공성 종단체는 수집 종단체의 항력을 줄이는 동시에 이상적으로 유사한 전류 수집을 유지하는 방법으로 제안되었다. 이들은 종종 고체 종단체로 모델링되지만, 고체 구의 표면적의 작은 부분에 해당한다. 그러나 이것은 개념을 극단적으로 단순화한 것이다. 시스 구조, 메시의 기하학적 구조, 종단체의 크기, 그리고 전류 수집과의 관계에 대해 많은 것을 배워야 한다. 이 기술은 또한 EDT와 관련된 여러 문제를 해결할 잠재력을 가지고 있다. 수집 전류와 항력 면적의 점진적 감소는 다공성 테더가 극복할 수 있는 한계를 설정했다. 스톤 외와 하자노프 외에 의해 다공성 구를 이용한 전류 수집에 대한 연구가 이루어졌다.

그리드 구에 의해 수집되는 최대 전류와 질량 및 항력 감소를 비교하여 추정할 수 있음이 밝혀졌다. 80~90%의 투명도를 가진 그리드 구의 단위 수집 전류당 항력은 동일한 반경을 가진 고체 구의 항력보다 약 1.2~1.4배 작다. 이 동일한 비교에서 단위 부피당 질량 감소는 2.4~2.8배이다.

기타 전류 수집 방법

전자 열 수집 외에도 EDT 시스템의 전류 수집에 영향을 미칠 수 있는 다른 과정으로는 광전 방출, 2차 전자 방출, 2차 이온 방출이 있다. 이러한 효과는 EDT 시스템의 모든 전도성 표면에 해당하며, 종단체에만 해당되는 것은 아니다.

플라스마 시스를 가로지르는 공간 전하 한계

전자가 진공 갭을 가로질러 방출되는 모든 응용 분야에서는 전자 빔의 자체 반발로 인해 주어진 바이어스에 대해 허용되는 최대 전류가 존재한다. 이 고전적인 1차원 공간 전하 한계(SCL)는 초기 에너지가 0인 전하 입자에 대해 유도되며, 차일드-랭뮤어 법칙이라고 불린다. 이 한계는 방출 표면적, 플라스마 갭을 가로지르는 전위차, 그리고 그 갭의 거리에 따라 달라진다. 이 주제에 대한 추가 논의는 다음에서 찾을 수 있다.

전자 방출기

EDT 응용 분야에서 일반적으로 고려되는 세 가지 능동 전자 방출 기술은 중공 음극 플라스마 접촉기(HCPC), 열전자 방출 음극(TC), 및 전계 방출 음극(FEC), 종종 전계 방출 배열(FEA)의 형태이다. 각 장치에 대한 시스템 수준 구성과 상대적인 비용, 이점 및 검증이 제시될 것이다.

열전자 음극(TC)

 이 부분의 본문은 열음극입니다.

열전자 방출은 가열된 전하를 띤 금속 또는 금속 산화물 표면에서 전자가 흐르는 현상으로, 열 진동 에너지가 일함수 (전자를 표면에 붙잡는 정전기력)를 극복하여 발생한다. 열전자 방출 전류 밀도 J는 온도가 증가함에 따라 빠르게 증가하며, 표면 근처의 진공으로 상당한 수의 전자를 방출한다. 정량적 관계는 다음 방정식으로 주어진다.

$J_{the}=A_{R}T^{2}e^{-\phi /(kt)}.$

이 방정식은 리처드슨-더쉬만 또는 리처드슨 방정식이라고 불린다. (ф는 약 4.54 eV이고 AR은 텅스텐의 경우 ~120 A/cm2이다.)

전자가 TC 표면에서 열전자 방출되면, 틈새를 가로지르거나, 이 경우 플라스마 시스를 가로지르기 위해 가속 전위가 필요하다. 가속 그리드 또는 전자총이 사용되면 전자는 플라스마 시스의 SCL을 탈출하는 데 필요한 에너지를 얻을 수 있다. 방정식

$\Delta V_{tc}=\left[{\frac {\eta \cdot I_{t}}{\rho }}\right]^{2/3}$

은 장치로 들어가는 특정 전류를 방출하기 위해 그리드에 필요한 전위가 무엇인지를 보여준다.

여기서 η는 전자총 조립체(EGA) 효율(~TSS-1에서 0.97), ρ는 EGA의 투과도(TSS-1에서 7.2 마이크로퍼브), ΔV_tc는 EGA의 가속 그리드에 걸리는 전압, I_t는 방출 전류이다. 투과도는 장치에서 방출될 수 있는 공간 전하 제한 전류를 정의한다. 아래 그림은 Heatwave Labs Inc.에서 생산된 열전자 방출기 및 전자총의 상업적 예시를 보여준다.

파일:Fig213 Electron Gun.PNG

전자 방출기의 예시: a) 열전자 방출기 및 b) 전자 가속 전자총 조립체

TC 전자 방출은 온도 또는 공간 전하 제한 전류 흐름이라는 두 가지 체제 중 하나에서 발생한다. 온도 제한 흐름의 경우, 음극 표면에서 탈출하기에 충분한 에너지를 얻는 모든 전자가 방출되며, 전자총의 가속 전위가 충분히 크다고 가정한다. 이 경우, 방출 전류는 리처드슨-더쉬만 방정식으로 주어지는 열전자 방출 과정에 의해 조절된다. SCL 전자 전류 흐름의 경우, 음극에서 너무 많은 전자가 방출되어 전자총에 의해 모두 충분히 가속되어 공간 전하를 탈출할 수 없다. 이 경우, 전자총 가속 전위가 방출 전류를 제한한다. 아래 차트는 온도 제한 전류와 SCL 효과를 보여준다. 전자의 빔 에너지가 증가함에 따라 총 탈출 전자가 증가하는 것을 볼 수 있다. 수평이 되는 곡선은 온도 제한 사례이다.

파일:Fig214 EGA Curve.PNG

진공 챔버에서 측정된 일반적인 전자 발생기 조립체(EGA) 전류-전압 특성

전계 방출 음극(FEC)

파일:Fig217 Field Emission.PNG

전계 방출

전계 전자 방출에서는 전자가 열전자 방출이나 광전 방출에서처럼 전위 장벽을 넘어가는 대신, 잠재 장벽을 통해 터널링한다. 저온 금속의 경우, 아래 그림을 통해 이 과정을 이해할 수 있다. 금속은 페르미 준위까지 전자로 채워진 전위 상자로 간주할 수 있다 (이는 진공 준위보다 몇 전자볼트 낮다). 진공 준위는 외부 전기장이 없을 때 금속 밖에 정지해 있는 전자의 전위 에너지를 나타낸다. 강한 전기장이 있을 때, 금속 밖의 전위는 선 AB를 따라 변형되어, 전자가 터널링할 수 있는 삼각형 장벽이 형성된다. 전자는 파울러-노르드하임 방정식으로 주어진 전류 밀도로 전도대에서 추출된다.

$J_{the}=A_{FN}\cdot E_{FN}^{2}\cdot e^{-B_{FN}/E_{FN}}.$

파일:Fig216 Field Emission.PNG

절대 영도 온도에서 금속으로부터의 전계 방출을 위한 에너지 준위도

AFN 및 BFN은 각각 A/V2 및 V/m 단위를 가진 FEA 측정으로 결정된 상수이다. EFN은 전자 방출 팁과 전자를 끌어내는 양전하 구조 사이에 존재하는 전기장이다. 스핀트 유형 음극의 일반적인 상수는 AFN = 3.14 x 10-8 A/V2 및 BFN = 771 V/m이다. (스탠포드 연구소 데이터 시트). 가속 구조는 일반적으로 아래 그림과 같이 방출 물질과 가까이 배치된다. 방출기와 게이트 사이의 근접성(마이크로미터 규모)은 자연 또는 인공적인 초점 구조와 결합되어 비교적 낮은 인가 전압 및 전력으로 방출에 필요한 높은 전장 강도를 효율적으로 제공한다.

탄소 나노튜브 전계 방출 음극은 일본 HTV-6에 탑재된 KITE 전기역학 테더 실험에서 성공적으로 테스트되었다.

전계 방출 음극은 종종 스핀트(Spindt) 등의 음극 설계와 같이 전계 방출 배열(FEA) 형태로 제공된다. 아래 그림은 스핀트 방출기의 근접 시각 이미지를 보여준다.

파일:Fig218 Field Emitter Array.PNG

전계 방출 배열의 확대 사진 (Capp Spindt가 ARPA/NRL/NASA 진공 마이크로일렉트로닉스 이니셔티브를 위해 개발한 SRI 링 음극의 SEM 사진)

실리콘에서부터 통합 게이트를 가진 반도체 제조 몰리브데넘 팁, 그리고 위에 매달린 별도의 게이트 구조를 가진 무작위 분포 탄소 나노튜브 판에 이르기까지 다양한 재료가 전계 방출 배열용으로 개발되었다. 대체 전자 방출 방법보다 전계 방출 기술의 장점은 다음과 같다.

1. 소모품(가스)이 필요 없고 가압 용기 취급에 대한 안전 고려 사항이 없다.
2. 저전력 기능
3. 주변 플라스마로의 전자 방출에서 공간 전하 한계로 인한 적당한 전력 영향이 있다.

전계 방출기에 대해 고려해야 할 주요 문제 중 하나는 오염의 영향이다. 낮은 전압에서 전자 방출을 달성하기 위해 전계 방출기 팁은 마이크로미터 수준의 크기로 제작된다. 성능은 이러한 작은 구조의 정밀한 구성에 따라 달라진다. 또한 낮은 일함수를 가진 재료로 제작되는지 여부에도 의존한다. 이러한 요인들은 장치를 오염, 특히 탄화수소 및 기타 크고 쉽게 중합되는 분자에 극도로 민감하게 만들 수 있다. 지상 테스트 및 전리층(예: 우주선 가스 방출) 환경에서 오염을 피하거나, 제거하거나, 존재하는 상태에서 작동하는 기술이 중요하다. 미시간 대학교 및 기타 기관의 연구는 이 가스 방출 문제에 중점을 두었다. 보호 인클로저, 전자 청소, 견고한 코팅 및 기타 설계 기능이 잠재적인 솔루션으로 개발되고 있다. 우주 응용 분야에 사용되는 FEA는 우주 응용 분야에 적합한 게이트 전위에서 장기적인 안정성, 반복성 및 작동 신뢰성 입증이 여전히 필요하다.

중공 음극

중공 음극은 먼저 가스를 이온화하여 밀도 높은 플라스마 구름을 방출한다. 이는 주변 플라스마와 접촉하는 고밀도 플라스마 플룸을 생성한다. 고밀도 플라스마 플룸과 주변 플라스마 사이의 영역은 이중 시스(double sheath) 또는 이중층(double layer)이라고 불린다. 이 이중층은 본질적으로 두 개의 인접한 전하 층이다. 첫 번째 층은 고전위 플라스마(접촉기 플라스마 구름) 가장자리의 양전하 층이다. 두 번째 층은 저전위 플라스마(주변 플라스마) 가장자리의 음전하 층이다. 이중층 현상에 대한 추가 조사는 여러 사람에 의해 수행되었다. 한 종류의 중공 음극은 소결 바륨 산화물 함침 텅스텐 인서트로 안감 처리된 금속 튜브로 구성되며, 한쪽 끝은 작은 오리피스가 있는 판으로 덮여 있다. 아래 그림에서 볼 수 있다. 전자는 바륨 산화물 함침 인서트에서 열전자 방출에 의해 방출된다. 불활성 기체가 HC의 인서트 영역으로 흐르고, 오리피스 근처의 전기장에 의해 가속되는 방출 전자에 의해 부분적으로 이온화된다(HC에 일반적으로 사용되는 제논은 비이온화 에너지(단위 질량당 이온화 전위)가 낮기 때문에 사용된다. EDT 목적의 경우, 총 시스템 질량이 적기 때문에 더 낮은 질량이 더 유익할 것이다. 이 기체는 전하 교환에만 사용되며 추진에는 사용되지 않는다.). 이온화된 제논 원자 중 상당수는 벽으로 가속되어 열전자 방출 온도를 유지한다. 이온화된 제논은 오리피스 밖으로도 방출된다. 전자는 인서트 영역에서 오리피스를 통해 키퍼로 가속되며, 키퍼는 항상 더 양극 편향되어 있다.

파일:Fig221 Hollow Cathode.PNG

중공 음극 시스템 개략도

전자 방출 모드에서 주변 플라스마는 키퍼에 대해 양전하를 띠게 된다. 접촉기 플라스마에서 전자 밀도는 이온 밀도와 거의 같다. 고에너지 전자는 천천히 팽창하는 이온 구름을 통해 흐르고, 저에너지 전자는 키퍼 전위에 의해 구름 내에 갇히게 된다. 높은 전자 속도는 제논 이온 전류보다 훨씬 큰 전자 전류로 이어진다. 전자 방출 포화 한계 미만에서 접촉기는 양극성 방출 탐침 역할을 한다. 전자에 의해 생성된 각 외부 이온은 여러 전자가 방출되도록 허용한다. 이 수는 이온 질량과 전자 질량의 비율의 제곱근과 거의 같다.

아래 차트에서 중공 음극의 전자 방출 모드에서 일반적인 I-V 곡선이 어떻게 나타나는지 볼 수 있다. 주어진 키퍼 형상(위 그림에서 전자가 나가는 고리), 이온 유량 및 Vp에 따라 I-V 프로파일을 결정할 수 있다. [111-113].

파일:Fig222 Hollow Cathode Curve.PNG

중공 음극의 일반적인 I-V 특성 곡선

전자 수집 모드에서 HC의 작동을 플라스마 접촉(또는 점화된) 작동 모드라고 부른다. "점화된 모드"는 플라스마 접촉기의 전압 강하를 사용하여 다중 암페어 전류 수준을 달성할 수 있음을 나타내기 때문에 그렇게 명명되었다. 이는 우주 플라스마 전자를 가속하여 접촉기에서 나오는 중성 발산 흐름을 이온화한다. 전자 수집 전류가 높거나 주변 전자 밀도가 낮은 경우, 전자 전류 수집이 유지되는 시스가 필요한 전류가 수집될 때까지 단순히 팽창하거나 수축한다.

또한, 아래 그림에서 볼 수 있듯이 형상이 HC에서 플라스마 방출에 영향을 미친다. 여기에서 키퍼의 직경과 두께, 그리고 오리피스에 대한 키퍼의 거리에 따라 총 방출 비율이 영향을 받을 수 있음을 알 수 있다.

파일:Fig223 Hollow Cathode Geometry.PNG

HC 방출 기하학을 상세히 설명하는 일반적인 개략도

플라스마 수집 및 방출 요약

모든 전자 방출 및 수집 기술은 다음 표에 요약되어 있다. 각 방법에는 우주선의 플라스마에 대한 전위에 따라 시스템 내 전자 또는 이온이 증가했는지 감소했는지에 대한 설명이 있다. 전자(e-) 및 이온(ions+)은 전자 또는 이온의 수가 증가(↑)하거나 감소(↓)하고 있음을 나타낸다. 또한, 각 방법에는 몇 가지 특별한 조건이 적용된다(적용 시기 및 장소에 대한 추가 설명은 이 문서의 해당 섹션 참조).

수동 e− 및 이온 방출/수집	V − Vp < 0	V − Vp > 0
베어 테더: OML	이온+ ↑	e− ↑
램 수집	이온+ ↑	0
열 수집	이온+ ↑	e− ↑
광전 방출	e− ↓	e− ↓,~0
2차 전자 방출	e− ↓	e− ↓
2차 이온 방출	이온+ ↓,~0	0
지연 체제	e− ↑	이온+ ↑, ~0
능동 e− 및 이온 방출	전위는 중요하지 않음
열전자 방출	e− ↓
전계 방출 배열	e− ↓
중공 음극	e− ↓	e− ↑

EDT 시스템 모델링에 사용하기 위해, 각 수동 전자 수집 및 방출 이론 모델은 이전에 발표된 방정식과 결과를 재현하여 검증되었다. 이러한 플롯에는 궤도 운동 제한 이론, 램 수집, 및 열 수집, 광전 방출, 2차 전자 방출, 및 2차 이온 방출이 포함된다.

전기역학 테더 시스템 기본 원리

가장 최신 전자 방출기, 수집기 및 이론을 단일 모델에 통합하려면 EDT 시스템을 먼저 정의하고 파생해야 한다. 이 작업이 완료되면 이 이론을 시스템 속성 최적화를 결정하는 데 적용할 수 있을 것이다.

EDT 시스템에 관련된 전위와 전류를 수치적으로 해결하는 여러 가지 유도법이 있다. 베어 테더 섹션, 절연 전도성 테더, 전자(및 이온) 종단체 방출기, 수동 전자 수집을 포함하는 완전한 EDT 시스템의 유도 및 수치 방법론이 설명된다. 이어서 단순화된 모든 절연 테더 모델이 이어진다. 특수 EDT 현상과 실험 임무 데이터를 사용한 EDT 시스템 모델의 검증이 논의될 것이다.

베어 테더 시스템 유도

EDT 유도에 관한 중요한 참고 사항은 테더 시스템이 궤도를 도는 천체에 관한 것이다. 실제적으로 지구는 궤도를 도는 천체로 사용될 것이지만, 이 이론은 전리층과 자기장을 가진 모든 천체에 적용된다.

좌표는 가장 먼저 식별되어야 할 사항이다. 이 유도 목적상, x축과 y축은 각각 지구 표면에 대한 동-서 및 북-남 방향으로 정의된다. z축은 아래 그림과 같이 지구 중심에서 위-아래로 정의된다. 매개변수—자기장 B, 테더 길이 L, 및 궤도 속도 v_orb—는 다음 방정식과 같이 이 좌표계로 표현될 수 있는 벡터이다.

$\mathbf {B} =B_{x}{\hat {x}}+B_{y}{\hat {y}}+B_{z}{\hat {z}}$ (자기장 벡터),

$\mathbf {L} =L\cos \alpha _{\mathrm {out} }\sin \alpha _{\mathrm {in} }{\hat {x}}+L\sin \alpha _{\mathrm {out} }{\hat {y}}+L\cos \alpha _{\mathrm {out} }\cos \alpha _{\mathrm {in} }{\hat {z}}$ (테더 위치 벡터), 및

$\mathbf {v} _{\mathrm {orb} }=v_{\mathrm {orb} }\cos \lambda _{\mathrm {out} }\sin \lambda _{\mathrm {in} }{\hat {x}}+v_{\mathrm {orb} }\sin \lambda _{\mathrm {out} }{\hat {y}}+v_{\mathrm {orb} }\cos \lambda _{\mathrm {out} }\cos \lambda _{\mathrm {in} }{\hat {z}}$ (궤도 속도 벡터).

자기장 구성 요소는 국제 지구 자기장 기준 모델 (IGRF) 모델에서 직접 얻을 수 있다. 이 모델은 자기장 모델러와 위성 및 전 세계 관측소 및 조사에서 자기장 데이터를 수집하고 배포하는 기관 간의 협력 노력으로 구성된다. 이 유도에서는 자기장 선이 테더 전체 길이에서 모두 같은 각도를 가지며 테더가 강체라고 가정한다.

궤도 속도 벡터

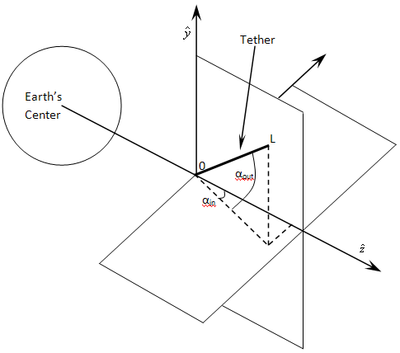
현실적으로, 횡단 전기역학적 힘은 테더를 휘게 하고 국부 수직선에서 벗어나게 한다. 중력 기울기 힘은 테더를 국부 수직선으로 다시 당기는 복원력을 생성하지만, 이는 진자 운동을 초래한다(중력 기울기 힘은 ED 힘 없이도 진자 운동을 초래한다). B 방향은 테더가 지구 궤도를 돌면서 변하므로, ED 힘의 방향과 크기도 변한다. 이 진자 운동은 면 내 및 면 외 방향 모두에서 복잡한 흔들림(libration)으로 발전할 수 있다. 그런 다음 면 내 운동과 종방향 탄성 진동 사이의 결합, 그리고 면 내 및 면 외 운동 사이의 결합으로 인해, 일정한 전류로 작동하는 전기역학 테더는 계속해서 흔들림 운동에 에너지를 추가할 수 있다. 이 효과는 흔들림 진폭을 증가시키고 궁극적으로 '줄넘기 효과'(skip-rope effect)와 같은 격렬한 진동을 유발할 수 있지만, 이는 이 유도의 범위를 벗어난다. 비회전 EDT 시스템(운동량 교환 전기역학 재부스트 [MXER]라고 불리는 회전 시스템)에서 테더는 지구와의 자연적인 중력 기울기 정렬로 인해 주로 z 방향에 있다.

= 파생

다음 유도는 관련된 모든 벡터량을 설명하는 시스템에 대한 정확한 해법을 설명하고, 그 다음에는 자기장, 궤도 속도 및 테더 방향이 모두 서로 수직인 명목 조건을 가진 두 번째 해법을 설명한다. 명목 사례의 최종 해법은 전자 밀도 n_e, 단위 길이당 테더 저항 R_t, 고전압 전원 공급 장치 P_hvps의 전력으로만 해결된다.

아래 그림은 전형적인 EDT 시스템을 직렬 바이어스 접지 게이트 구성(분석된 다양한 구성 유형에 대한 추가 설명은에 제시됨)으로 보여주며, 베어 테더의 무한소 단면의 확대도를 포함한다. 이 그림은 양쪽 끝을 양극으로 사용할 수 있도록 대칭적으로 설정되어 있다. 이 테더 시스템은 회전하는 테더 시스템이 회전 중 어느 시점에서든 양쪽 끝을 양극과 음극으로 사용해야 하기 때문에 대칭적이다. V_hvps는 EDT 시스템의 음극 끝에서만 사용되며, 그렇지 않으면 꺼진다.

(a) 베어 테더 세그먼트의 회로도와 (b) 직렬 바이어스 접지 게이트 구성을 보여주는 등가 EDT 시스템 회로 모델

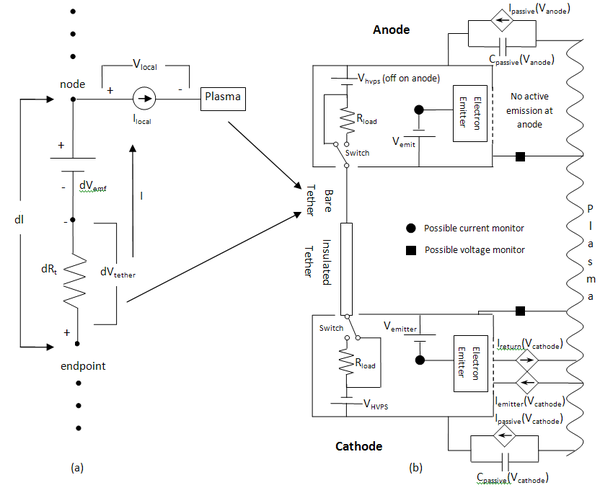
면 내 및 면 외 방향은 시스템의 궤도 속도 벡터에 의해 결정된다. 면 내 힘은 이동 방향과 일치한다. 이는 궤도에 에너지를 추가하거나 제거하여 궤도를 타원형으로 변경함으로써 고도를 증가시킨다. 면 외 힘은 이동 평면에 수직인 방향으로 작용하며, 이는 경사각을 변경한다. 이는 다음 섹션에서 설명될 것이다.

면 내 및 면 외 방향을 계산하려면 속도 및 자기장 벡터의 구성 요소를 얻고 힘 값을 계산해야 한다. 이동 방향의 힘 구성 요소는 궤도 상승 능력을 향상시키는 역할을 하며, 추력의 면 외 구성 요소는 경사각을 변경한다. 아래 그림에서 자기장 벡터는 오로지 북쪽(또는 y축) 방향에만 있으며, 특정 경사각을 가진 궤도에 작용하는 결과적인 힘을 볼 수 있다. 경사각이 없는 궤도는 모든 추력이 면 내 방향으로 작용할 것이다.

면 내 및 면 외 힘의 설명

파일:Fig35 Orbit Drag.PNG 전기역학 테더 시스템에 대한 항력 효과

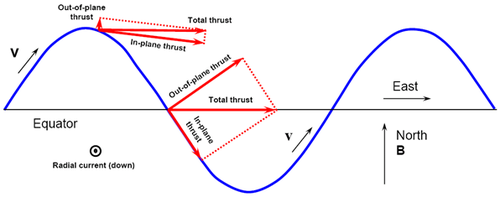테더가 중력 기울기와 정렬되지 않도록 하는 테더 시스템의 흔들림을 안정화하기 위한 연구가 진행되었다. 아래 그림은 EDT 시스템이 일반적인 궤도에서 겪게 될 항력 효과를 보여준다. 면 내 각도 α_ip와 면 외 각도 α_op는 시스템의 최종 질량을 증가시키거나 피드백 기술을 사용하여 줄일 수 있다. 중력 정렬의 모든 편차를 이해하고 시스템 설계에 고려해야 한다.

성간 이동

 이 부분의 본문은 성간 이동입니다.

EDT 시스템의 한 응용 분야는 국부 거품의 국부 성간 매질을 이용하여 성간 이동을 위해 고려되고 연구되었다. 승무원 50명에게 1인당 12킬로와트의 전력 요구량을 감안할 때 EDT 시스템이 탑재 전력을 공급하는 것이 실행 가능하다고 밝혀졌다. 에너지 생성은 우주선의 운동 에너지를 희생하여 이루어진다. 반대로 EDT 시스템은 가속에 사용될 수 있다. 그러나 이것은 비효율적인 것으로 밝혀졌다. EDT 시스템을 이용한 무추력 선회는 성간 공간에서 경로 수정 및 랑데부를 가능하게 한다. 그러나 3.7*10¹³km (약 3.7 광년)의 매우 큰 선회 반경으로 인해 우주선이 전력 빔에 다시 진입하거나 수많은 태양 통과를 수행하는 것을 허용하는 빠른 무추력 선회는 불가능하다.

같이 보기

• STARS-II
• HTV-6
• 테더 추진
• 지자기
• 테더 위성
• 대기전기학
• STS-75
• 자기 돛
• 전기 돛
• 우주선 추진

각주

일반 정보

• Cosmo, M.L., and Lorenzini, E.C., "Tethers in Space Handbook," NASA Marchall Space Flight Center, 1997, pp. 274–1-274.
• Mariani, F., Candidi, M., Orsini, S., "Current Flow Through High-Voltage Sheaths Observer by the TEMAG Experiment During TSS-1R," Geophysical Research Letters, Vol. 25, No. 4, 1998, pp. 425–428.

인용

더 읽어보기

• Dobrowolny, M. (1979). Wave and particle phenomena induced by an electrodynamic tether. SAO special report, 388. Cambridge, Mass: Smithsonian Institution Astrophysical Observatory.
• Williamson, P. R. (1986). High voltage characteristics of the electrodynamic tether and the generation of power and propulsion final report. [NASA contractor report], NASA CR-178949. Washington, DC: National Aeronautics and Space Administration.

외부 링크

관련 특허

• 미국 특허 3,174,705, "Space station and system for operating same".
• 미국 특허 3,205,381, "Ionospheric battery".
• 미국 특허 4,097,010, "Satellite connected by means of a long tether to a powered spacecraft ".
• 미국 특허 6,116,544, "Electrodynamic Tether And Method of Use".

출판물

• Samanta Roy, R.I.; Hastings, D.E.; Ahedo, E. (1992). “Systems analysis of electrodynamic tethers”. 《J Spacecr Rockets》 29 (3): 415–424. Bibcode:1992JSpRo..29..415S. doi:10.2514/3.26366. 
• Ahedo, E.; Sanmartin, J.R. (March–April 2002). “Analysis of bare-tethers systems for deorbiting Low-Earth-Orbit satellites”. 《J Spacecr Rockets》 39 (2): 198–205. Bibcode:2002JSpRo..39..198A. doi:10.2514/2.3820. 
• Peláez, J.; Sánchez-Arriaga, G.; Sanjurjo-Rivo, M. (October 2012). 《Self balanced electrodynamic tethers for space debris mitigatation》. 57th International Astronautical Conference. Valencia, Spain: AIAA. doi:10.2514/6.IAC-06-B6.4.03. ISBN 978-1-62410-042-0. 2022년 11월 6일에 확인함. 
• Cosmo, M. L., and E. C. Lorenzini, "Tethers in Space Handbook" (3rd ed). Prepared for NASA/MSFC by Smithsonian Astrophysical Observatory, Cambridge, MA, December 1997. (PDF)
• Estes, R.D.; Lorenzini, E.C.; Sanmartín, J.R.; Martinez-Sanchez, M.; Savich, N.A. (December 1995). “New High-Current Tethers: A Viable Power Source for the Space Station? A White Paper” (PDF). 2006년 2월 18일에 원본 문서 (PDF)에서 보존된 문서. 
• Savich, N.A.; Sanmartín, J.R. (1994). 〈Short, High Current Electrodynamic Tether〉. 《Proc. Int. Round Table on Tethers in Space》. 417쪽. 
• McCoy, James E. 외 (April 1995). 〈Plasma Motor-Generator (PMG) Flight Experiment Results〉. 《Proceedings of the 4th International conference on Tethers in Space》. Washington DC. 57–84쪽. 

기타 문서

• "Electrodynamic Tethers 보관됨 2011-05-17 - 웨이백 머신". Tethers.com.
• "Shuttle Electrodynamic Tether System (SETS)".
• Enrico Lorenzini and Juan Sanmartín, "Electrodynamic Tethers in Space; By exploiting fundamental physical laws, tethers may provide low-cost electrical power, drag, thrust, and artificial gravity for spaceflight". Scientific American, August 2004.
• "Tethers". Astronomy Study Guide, BookRags.
• David P. Stern, "The Space Tether Experiment". 25 November 2001.