조지프슨 전압 표준

조지프슨 전압 표준(영어: Josephson voltage standard)은 4 K의 온도에서 작동하는 초전도 집적회로 칩을 사용하여 인가된 주파수와 기본 상수에만 의존하는 안정적인 전압을 생성하는 복잡한 시스템이다. 이는 어떤 물리적 인공물에도 의존하지 않는다는 점에서 본질적인 표준이다. 이것은 전압을 생성하거나 측정하는 가장 정확한 방법이며, 1990년 국제 협약 이후 전 세계 전압 표준의 기반이 되어 왔다.

조지프슨 효과

1962년 케임브리지 대학교의 대학원생이었던 브라이언 데이비드 조지프슨은 두 초전도체를 분리하는 얇은 절연 장벽으로 구성된 접합부(현재는 일반적으로 조지프슨 접합이라고 알려져 있음)를 가로지르는 전류와 전압에 대한 방정식을 유도했다.^[1] 그의 방정식은 접합부가 주파수 $f$ 에서 구동될 때, 전류-전압(I–V) 곡선이 $nhf/2e$ 값에서 일정한 전압 영역을 형성할 것이라고 예측했다. 여기서 $n$ 은 정수이고 $h/e$ 는 플랑크 상수 $h$ 와 기본 전하 $e$ 의 비율이다. 이 예측은 1963년 샤피로(Shapiro)에 의해 실험적으로 검증되었으며^[2] (역) AC 조지프슨 효과로 알려지게 되었다. 이 효과는 전압을 기본 상수에만 관련된 비례 관계를 통해 초와 연관시키기 때문에 도량형학에 즉시 적용되었다. 처음에는 이것이 비율 $h/e$ 의 개선된 값으로 이어졌다. 오늘날 이것은 모든 기본 전압 표준의 기반이다. 초전도 터널 접합을 통한 초전류에 대한 조지프슨 방정식은 다음과 같이 주어진다.

I=I_{\text{c}}\sin {\Bigl (}{4\pi e \over h}\int Vdt{\Bigr )}

여기서 $I$ 는 접합 전류, $I_{\text{c}}$ 는 임계 전류, $V$ 는 접합 전압이다. $I_{\text{c}}$ 는 접합부 형상, 온도, 전압 표준 장치에 사용되는 자기 차폐 내부의 잔류 자기장에 따라 달라진다. 접합부에 DC 전압이 인가되면 Eq. (1)은 전류가 주파수 $f_{\text{J}}=2eV/h$ 로 진동할 것이며, 여기서 $2e/h$ 는 약 484 GHz/mV와 같다는 것을 보여준다. 이 진동의 매우 높은 주파수와 낮은 수준 때문에 직접 관찰하기 어렵다. 그러나 주파수 $f$ 의 AC 전류가 접합부에 인가되면 접합 진동 $f_{\text{J}}$ 는 인가된 주파수에 위상 동기화되는 경향이 있다. 이 위상 동기화 하에서, 접합부의 평균 전압은 $hf/2e$ 와 같다. (역) AC 조지프슨 효과로 알려진 이 효과는 접합부의 전압-전류(I–V) 곡선에서 $V=hf/2e$ 에서 일정한 전압 스텝으로 관찰된다. 접합부가 $f$ 의 고조파에 위상 동기화될 수도 있다. 이것은 그림 1a에 표시된 것처럼 $V=nhf/2e$ (여기서 $n$ 은 정수) 전압에서 일련의 스텝을 초래한다.

조지프슨 효과는 처음에는 웨스턴 전지에 의해 유지되는 SI 볼트 구현에서 파생된 전압 값을 기반으로 상수 $2e/h$ 의 측정을 개선하는 데 사용되었다. 이러한 측정의 불확실성은 SI 볼트 구현의 불확실성과 웨스턴 전지의 안정성에 의해 제한되었다.^[3]^[4] 조지프슨 볼트의 안정성은 $f$ 의 안정성(10¹²분의 1만큼 쉽게 가능함)에만 의존하며, 웨스턴 전지의 안정성보다 최소 4자리 이상 좋다. 따라서 1970년대 초, 많은 국가 표준 연구소는 조지프슨 상수 $K_{\text{J}}=2e/h$ 의 값을 채택하고 (역) AC 조지프슨 효과를 전압의 실용 표준으로 사용하기 시작했다.^[5]^[6] 기존 국가 표준의 작은 차이 때문에 여러 국가에서 다른 $K_{\text{J}}$ 값이 채택되었다. 이 불일치는 1990년에 국제 협약에 의해 상수 $K_{\text{J-90}}$ 에 483597.9 GHz/V 값이 할당되고 모든 표준 연구소에서 채택되면서 수정되었다.^[7] 할당된 값은 1990년 이전에 많은 국가 측정 기관에서 수행된 볼트 구현 측정의 가중 평균을 기반으로 한다. $K_{\text{J-90}}$ 의 불확실성은 0.4 ppm이다. 물리적 인공물이 아닌 기본 상수에 의존하는 조지프슨 볼트와 같은 표준은 본질적인 표준으로 알려져 있다. 조지프슨 전압 표준(JVS)이 볼트의 SI 정의를 구현하지는 않지만, 웨스턴 전지와 같은 인공물을 옮길 필요 없이 어디서든 재현할 수 있는 매우 안정적인 기준 전압을 제공한다. 조지프슨 전압-주파수 관계 $V=nf/K_{\text{J}}$ 의 정확성과, 바이어스 전류, 온도, 접합 재료와 같은 실험 조건에 대한 독립성은 많은 테스트를 거쳤다. 이 관계에서 유의미한 편차는 발견되지 않았다.^[8] 이 실험들 중 가장 정밀한 실험에서는 두 개의 조지프슨 장치가 동일한 주파수 소스에 의해 구동되고, 동일한 스텝에 바이어스되며, 작은 인덕터에 걸쳐 직렬 반대 루프로 연결된다. 이 루프는 완전히 초전도이므로, 어떤 전압 차이도 인덕터의 자기장 변화로 이어진다. 이 자기장은 SQUID 자력계로 감지되며, 그 일정성은 전압 차이에 대해 10¹⁹분의 3 미만의 상한선을 설정했다.^[9]^[10] 그림 2는 지난 70년 동안 국가 측정 기관(NMI) 간의 DC 전압 측정에서 전형적인 차이가 어떻게 감소했는지 보여주는 반대수 그림이다.^[11] 두 가지 주요 개선은 1970년대 초 단일 접합 조지프슨 표준의 도입과 1984년에 시작된 직렬 배열 조지프슨 표준의 도입과 일치한다.

초기 조지프슨 표준

AC 조지프슨 효과는 웨스턴 전지보다 훨씬 더 안정적인 전압 기준을 제공하지만, 첫 번째 단일 접합 조지프슨 표준은 매우 작은 전압(1–10 mV)을 생성했기 때문에 사용하기 어려웠다. 두 개 이상의 접합부를 직렬로 연결하여 전압을 높이려는 여러 시도가 있었다. 이 중 하나는 20개의 접합부를 직렬로 사용하여 10⁹분의 몇 배의 불확실성으로 100 mV의 전압을 구현했다.^[12] 각 접합부가 일정한 전압 스텝에 있도록 보장하려면 20개의 접합부 각각에 대해 바이어스 전류를 개별적으로 조정해야 했다. 이 절차의 어려움 때문에 20개 이상의 접합부 배열은 비실용적이다.

1977년 레빈슨 등은^[13] 궁극적으로 다중 바이어스 문제의 해결책으로 이어질 제안을 했다. 레빈슨은 RF 유도 조지프슨 스텝의 특성을 결정하는 데 매개변수 $\beta _{\text{c}}=4\pi eI_{\text{c}}R^{2}C/h$ 의 중요성을 지적했다. $\beta _{\text{c}}$ 는 접합부 션트 저항 $R$ 에 의한 조지프슨 진동의 감쇠를 측정하는 값이다. 특히, 그는 큰 정전 용량 $C$ 와 큰 $R$ ( $\beta _{\text{c}}>100$ )을 가진 접합부가 그림 1b에 표시된 것과 같은 이력적인 정전압 스텝을 가진 I–V 곡선을 생성할 수 있음을 보여주었다. 이 스텝들은 I–V 곡선의 영전류 축을 가로지르기 때문에 영교차 스텝으로 알려지게 되었다. 처음 몇 스텝 사이에 안정적인 영역이 없다는 것은 작은 DC 바이어스 전류의 경우 접합 전압이 양자화되어야 함을 의미한다. 영 또는 영에 가까운 공통 바이어스 전류를 사용하면, 이러한 접합부의 큰 배열에 걸쳐 있는 전압도 양자화되어야 한다. 넓은 범위의 접합부 및 작동 매개변수에서 영전류에서 정전압 스텝을 얻을 가능성은 많은 접합부 배열을 사용하여 전압 표준을 구축할 가능성을 시사했다.

몇 가지 예비 실험 후,^[14]^[15]^[16] 1984년 미국 국립표준국과 독일의 물리기술연구원 간의 공동 노력으로 접합 안정성과 마이크로파 분배 문제를 해결하고 레빈슨의 아이디어를 기반으로 한 최초의 대형 조지프슨 배열을 만들었다.^[17] 추가적인 설계 개선과 시스템 개발로 1985년 최초의 실용적인 1V 조지프슨 표준이 만들어졌다.^[18]^[19]

조지프슨 접합 컴퓨터를 위한 탐구에 의해 크게 주도된 초전도 집적회로 기술의 발전은^[20] 곧 훨씬 더 큰 배열을 가능하게 했다. 1987년에는 이 설계가 14484개의 접합부를 가진 칩으로 확장되어 −10 V에서 +10 V 범위에 걸쳐 약 150000개의 양자화된 전압을 생성했다.^[21] 10V 조지프슨 표준이 많은 국가 표준 연구소에 구현되면서 수많은 추가 개선이 이루어졌다.^[22] 1989년까지 완전한 전압 측정 시스템을 위한 모든 하드웨어와 소프트웨어가 상업적으로 이용 가능했다. 오늘날 전 세계 70개 이상의 국가, 산업 및 군사 표준 연구소에 조지프슨 배열 전압 표준이 있다. 국제 도량형국(BIPM)에서 수행하는 국제 비교 프로그램은 이동식 조지프슨 표준과 NMI 간의 차이를 측정했으며, 이는 일반적으로 10⁹분의 1 미만이다.^[23]^[24]

접합 설계 세부 사항

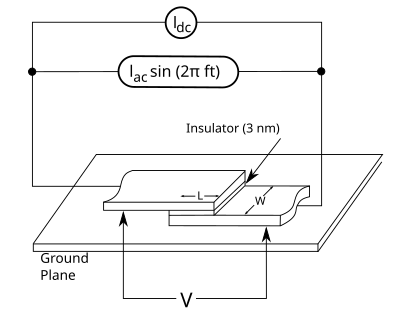
그림 3은 대형 직렬 배열의 한 접합부의 기본 구조를 보여준다. 접합부는 두 초전도 박막이 얇은 산화물 장벽으로 분리되어 겹쳐진 부분이다. 접합부는 접지면 위에 놓여 있으며, 몇 마이크로미터의 절연체로 분리되어 있다. DC 전류 $I_{\text{dc}}$ 와 마이크로파 전류 $I_{\text{ac}}$ 는 접합부를 통해 흐른다. 접합부의 설계 매개변수는 길이 $L$ , 폭 $W$ , 임계 전류 밀도 $J$ (단위 면적당 임계 전류) 및 마이크로파 구동 주파수 $f$ 이다. 배열 전압 표준의 실제 구현은 이러한 매개변수가 그림 1b에 표시된 양자화된 전압 레벨의 안정성에 어떻게 영향을 미치는지에 대한 철저한 이해를 필요로 한다. 안정적인 작동을 위해서는 다음 네 가지 조건을 충족해야 한다.

$L$ 은 마이크로파 자기장에 의해 접합부 면적을 통해 유도되는 플럭스가 플럭스 양자 $h/2e$ 보다 훨씬 작을 만큼 작아야 한다.
$W$ 와 $L$ 모두 접합부의 최저 공진 공동 모드가 $f$ 보다 클 만큼 작아야 한다.
혼란스러운 동작을 피하기 위해 ${\sqrt {J}}$ 에 비례하는 접합 플라즈마 주파수 $f_{\text{p}}$ 는 $f$ 의 약 1/3보다 작아야 한다.
노이즈 유도 양자 스텝 전환을 방지하기 위해 접합부의 임계 전류 $I_{\text{c}}=WLJ$ 는 가능한 한 커야 한다.

이러한 조건 중 하나라도 위반되면 접합 전압이 여러 스텝 사이에서 무작위로 전환되어 측정이 불가능해질 가능성이 있다. 이러한 조건에 대한 엄밀한 유도는 카우츠(Kautz)의 여러 논문 주제이다.^[25]^[26]

그림 4는 $L$ , $W$ , $J$ 의 3차원 공간에서 안정적인 동작 영역을 보여준다. 그림 4의 음영 처리된 볼륨으로 표현되는 안정적인 작동 마진은 $f$ 에 따라 증가하며, 궁극적으로 안정성과 매우 높은 주파수 마이크로파 소스를 제공하는 경제성 사이의 절충점에 의해 결정된다. 24 GHz와 같이 낮은 주파수에서도 안정적인 배열이 시연되었지만,^[27]^[28] 대부분의 실용적인 표준은 70–96 GHz 범위에서 작동한다. 표 1은 일반적으로 사용되는 설계에 대한 일반적인 접합 매개변수 집합을 나열한다.

일반적인 접합 매개변수
접합 재료	Nb/Al₂O₃/Nb
임계 전류 밀도 J	20 A/cm²
접합 길이 L	18 μm
접합 폭 W	30 μm
임계 전류 I₀	110 μA
플라즈마 주파수 f_p	20 GHz
최저 공진 공동 모드	175 GHz
RF 구동 주파수 f	75 GHz

배열 설계

그림 1b에 표시된 I–V 곡선은 약 −1 mV에서 +1 mV 범위에 걸쳐 있는 스텝을 보여주며, 이는 거의 최적의 마이크로파 전류 수준으로 구동되는 접합부에 대한 것이다. 낮은 마이크로파 전류에서는 스텝이 더 작은 전압 범위를 커버하고, 높은 마이크로파 전류에서는 스텝이 작아지고 영전류 축에서 벗어나기 시작한다. 대형 배열에서는 모든 접합부가 큰 영교차 스텝을 생성해야 하므로, 마이크로파 전력은 가장 큰 마이크로파 구동을 받는 한 접합부에 맞출 수 있을 만큼 낮은 값으로 조정되어야 한다. 따라서 가장 적은 수의 접합부에서 가장 큰 전압을 얻기 위해서는 배열 표준이 수천 개의 접합부에 거의 균일한 마이크로파 전력을 전달할 수 있는 회로 설계를 필요로 한다. 이 접합부들은 모두 직렬로 연결되어 있다. 이 문제의 해결책은 그림 3을 그림 5a에 표시된 것처럼 접지면 위에 일렬로 배열된 접합부들의 직렬 연결로 간단히 확장하는 것이다. 이는 상대적으로 낮은 손실로 마이크로파 전력을 전파할 수 있는 마이크로파 스트립라인을 만든다. 접합부의 용량성 임피던스는 스트립라인 임피던스(약 3 Ω)에 비해 매우 작아서(약 1 mΩ) 각 접합부가 스트립라인의 마이크로파 전력 전파에 미치는 영향이 매우 미미하다. 일반적으로 각 접합부는 통과하는 전력의 약 0.02%에서 0.04%를 흡수한다. 따라서 수천 개의 접합부를 직렬로 연결하고도 약 ±1.5 dB의 전력 균일도를 달성할 수 있다. 신중한 설계를 통해 최대 4800개의 접합부를 가진 스트립라인이 사용되었다.^[29]

10 V 조지프슨 표준은 약 20000개의 접합부를 필요로 하기 때문에, 그림 5b에 나타낸 것과 유사한 직렬/병렬 회로를 채택할 필요가 있다.^[39] 여기서 저역 및 고역 통과 필터 네트워크는 마이크로파 전력을 4개의 병렬 경로로 분할하면서 모든 접합부가 직렬로 연결된 DC 경로를 유지하게 한다.

20208개 접합부 배열의 전형적인 집적회로 레이아웃은 그림 6에 나와 있다. 마이크로파 구동 전력은 도파관에서 핀라인 안테나에 의해 수집되고, 16갈래로 분할되어 각각 1263개의 접합부를 가진 16개의 접합부 스트립 라인으로 주입된다. 접합부 스트립 라인은 약 2 마이크로미터의 SiO₂ 유전체에 의해 초전도 접지면과 분리되어 있다. 분할 네트워크의 대칭성은 각 서브어레이에 동일한 전력이 전달되도록 보장한다. 정재파와 그에 따른 서브어레이 내의 불균일한 전력 분포를 초래할 수 있는 반사를 피하기 위해 몇 가지 주의 사항이 필요하다.

각 스트립라인은 여러 파장의 저항성 스트립라인으로 구성된 정합 부하로 종단된다. 개별 저항 대신 저항성 스트립라인을 사용하면 넓은 범위의 제조 매개변수에서 거의 완벽한 정합을 보장한다.
저역 및 고역 통과 필터의 커패시터 크기는 구동 주파수 근처의 공진을 피하도록 선택된다.
마이크로파 굽힘 반경은 스트립라인 폭의 최소 3배이다. 더 급한 굽힘은 용납할 수 없는 반사를 초래한다. 굽힘 요구 사항을 충족하면서 배열 스트립을 가깝게 배치하기 위해 215° 회전한 다음 45° 뒤로 돌아가는 "컬리(curly)" 굽힘이 사용된다.
라인을 따라 접합부 간의 간격은 인접 접합부 간의 공진을 피할 만큼 충분히 가까워야 한다.^[30] 마이크로파 전력은 칩의 핀라인 끝을 WR-12 도파관의 E-필드와 평행한 슬롯에 삽입하여 인가된다. DC 출력은 칩 가장자리의 초전도 패드를 가로질러 나타난다.

제조

전압 표준 칩은 일반적으로 실리콘 또는 유리 기판에 제조된다. 집적회로는 8개의 층으로 구성된다.

300 nm 두께의 Nb 접지면,
마이크로스트립라인 유전체를 형성하는 2 μm 두께의 SiO₂ 층,
조지프슨 접합의 하부 전극을 형성하는 200 nm Nb 박막,
조지프슨 터널링 장벽을 형성하는 3 nm 금속 산화물 층,
100 nm Nb 접합 상부 전극,
상부 전극과의 접촉을 위한 창문이 있는 300 nm SiO₂ 박막,
접합 상부 전극을 연결하는 400 nm Nb 박막, 그리고
스트립라인 종단을 형성하는 100 nm 저항성 박막.

측정 시스템

현대 조지프슨 전압 표준 시스템의 블록 다이어그램은 그림 7에 나와 있다. 조지프슨 배열 칩은 액체 헬륨 듀어와 실온 환경 사이의 전환을 만드는 극저온 프로브 끝에 있는 높은 투자율의 자기 차폐 내부에 장착된다. 일부 시스템은 극저온 냉각기를 사용하여 칩을 냉각하고 액체 헬륨의 필요성을 없앤다. 세 쌍의 구리선이 배열에 연결된다. 한 쌍은 바이어스 전류를 공급하고, 두 번째 쌍은 오실로스코프로 배열 전압을 모니터링하며, 세 번째 쌍은 배열 전압을 보정 시스템으로 전달한다. 모든 전선은 듀어 상단의 상자에 있는 여러 수준의 RFI 필터링을 통과한다. 상자, 필터 및 듀어 자체는 조지프슨 배열을 스텝 전환을 유발할 수 있는 전자기 간섭으로부터 보호하는 차폐막을 형성한다. 마이크로파 전력은 각 끝에 WR-12 발사 혼이 있는 12 mm 직경 튜브로 구성된 도파관을 통해 전달된다. 속이 빈 양은 또는 내부에 은이나 금으로 도금된 스테인리스 스틸 튜브가 일반적으로 사용된다. 이 도파관은 동시에 낮은 열 손실(하루 0.5 L 미만의 액체 He)과 낮은 마이크로파 손실(75 GHz에서 0.7 dB만큼 낮음)을 달성한다.

75 GHz 근처의 주파수에서 작동하는 위상 고정 발진기(PLO)는 칩에 마이크로파 전력을 제공한다. 75 GHz 소스의 주요 요구 사항은 다음과 같다. (1) 주파수가 높은 정확도(10¹⁰분의 1)로 알려져야 하며 (2) 최소 50 mW(+17 dBm)의 안정적인 출력 전력을 생산해야 한다. 소스를 다양한 주파수 범위에 걸쳐 튜닝할 수 있는 것이 유용하지만 필수적이지는 않다. PLO는 상업용 마이크로파 카운터에 피드백 기능을 추가하여 구성하거나 맞춤형 위상동기회로로 만들 수 있다. 최근에는 더 신뢰할 수 있고 더 넓은 튜닝 범위와 해상도를 제공하는 마이크로파 주파수 신디사이저가 선호되는 마이크로파 소스가 되었다. 시스템의 주파수 참조는 일반적으로 GPS 수신기 또는 원자 시계에서 파생된 10 MHz 사인파이다.

그림 1b의 영교차 스텝은 전체 접합 배열을 통과하는 단일 바이어스 전류를 허용하면서 배열의 모든 접합부가 일정한 전압 스텝에 있도록 보장한다. 이로 인해 배열을 특정 원하는 스텝으로 설정하는 데 상당한 복잡성이 발생한다. 그림 8a는 바이어스 회로의 간략화된 다이어그램을 보여준다. 이 회로에서 컴퓨터는 하나의 디지털-아날로그 변환기(DAC)로 바이어스 전압 $V_{\text{s}}$ 를 설정하고 두 번째 DAC를 사용하여 광 변조 저항을 통해 바이어스 임피던스 $R_{\text{s}}$ 를 제어한다. 그림 8b는 배열의 안정적인 작동 지점에 대한 그래픽 솔루션을 보여주며, 바이어스 전압과 바이어스 임피던스 제어를 사용하여 특정 양자 전압 스텝을 선택하는 방법을 보여준다.^[31]

부하선은 바이어스 전원에 의해 정의되는 전압 및 전류 범위를 나타낸다. 이 부하선과 배열의 I–V 곡선(수직선)의 교차점은 가능한 안정적인 바이어스 지점이다. $V_{\text{s}}$ 의 변화는 부하선을 좌우로 이동시키고, $R_{\text{s}}$ 의 변화는 기울기를 변경한다. 주어진 전압 $V_{\text{a}}$ 에서 스텝을 선택하려면, 소스 전압을 $V_{\text{a}}$ 로 설정하고 소스 임피던스를 약 $f/K_{\text{J}}I_{\text{s}}=10\Omega$ 로 설정한다. 여기서 $I_{\text{s}}$ 는 스텝 높이다. 이렇게 하면 부하선이 하나 또는 두 개의 스텝만 교차할 만큼 가파르게 되어 배열을 $V_{\text{a}}$ 또는 그 근처의 스텝으로 강제한다. $V_{\text{a}}$ 에 감쇠 진동을 가하면 배열을 $V_{\text{a}}$ 에 가장 가까운 스텝으로 이동시키는 데 도움이 된다. 스텝이 선택되면, 배열 전류가 영이 되고 배열이 바이어스 소스에서 효과적으로 분리될 때까지 네 개의 바이어스 연결 모두에서 소스 임피던스가 부드럽게 증가한다(부하선이 수직이 됨). 이 개방 바이어스 조건은 배열에 가장 안정적인 상태이며, 배열의 작은 직렬 저항으로 인한 오류 가능성을 제거한다 – 일반적인 배열 결함이다. 이 세 단계 과정의 컴퓨터 제어를 통해 시스템은 몇 초 이내에 특정 스텝에서 배열 전압을 찾아 안정화할 수 있다. 고품질 조지프슨 배열은 선택된 스텝에 여러 시간 동안 유지될 것이다.

조지프슨 표준을 보조 표준 또는 다른 조지프슨 표준과 비교하기 위한 수많은 알고리즘이 개발되었다. 이러한 알고리즘은 사용되는 평균화 양, 반전 스위치의 유형 및 배치, 데이터를 줄이고 불확실성을 계산하는 데 사용되는 통계 방법이 다르다. 알고리즘 선택은 비교 유형, 원하는 불확실성 수준 및 사용 가능한 시간에 따라 달라진다. 제너 참조 표준의 교정에 적합한 일반적으로 사용되는 알고리즘 중 하나는 여기에 설명되어 있다.

측정 알고리즘 예시

조지프슨 배열 전압에 대한 미지 참조 $V_{\text{R}}$ 의 전압은 그림 9(그림 7의 하위 집합)에 표시된 회로를 사용하여 결정된다. 이 회로에서는 미지 참조와 조지프슨 배열이 널 미터(null meter)에 걸쳐 직렬 반대로 연결된다. 반전 스위치는 열 및 기타 오프셋 전압의 영향을 제거하는 데 사용된다. 스텝 번호 $n$ 과 때로는 주파수 $f$ 는 널 전압을 가능한 한 작게 만들기 위해 조정된다. 회로 방정식은 다음과 같이 쓸 수 있다.

{\begin{aligned}V_{\text{a}}-V_{\text{null}}&=nf/K_{\text{J}}-V_{\text{null}}\\&=PV_{\text{R}}-V_{0}-mt-V_{\text{noise}}\end{aligned}}

여기서, $V_{\text{a}}=nf/K_{\text{J}}$ 는 조지프슨 배열 전압이고, V₀는 열 오프셋 전압과 널미터의 모든 오프셋 전압의 조합이며, mt는 오프셋 전압의 선형 드리프트 성분을 나타내고, $P=\pm 1$ 는 반전 스위치의 극성이고, $V_{\text{null}}$ 은 차동 널 전압이며, $V_{\text{noise}}$ 는 미지, 널미터 및 기타 무작위 노이즈 소스의 노이즈를 나타낸다. 이제 매개변수 $V_{\text{i}}=nf/K_{\text{J}}-V_{\text{null}}$ 를 정의한다. 여기서 $V_{\text{null}}$ 은 시간 $t_{\text{i}}$ 에서의 측정값이고 $n$ 은 $V_{\text{null}}$ 로부터 다음과 같이 결정된다.

n=\operatorname {Round} {(K_{\text{J}}/f)(V_{\text{e}}+V_{\text{null}})}

여기서 $V_{\text{e}}$ 는 시스템 전압계에 의한 $V_{\text{R}}$ 의 초기 직접 측정값이고 "Round" 함수는 가장 가까운 정수로 반올림하는 것을 의미한다. $V_{\text{R}}$ 의 직접 측정값은 배열을 $n=0$ 스텝으로 설정하여 얻어진다. 이는 그림 7에서 전압계를 제너 기준에 직접 연결하는 것을 볼 수 있다.

$V_{\text{e}}$ 와 $V_{\text{null}}$ 의 측정값을 기반으로 $P=+1$ 에 대한 $V_{\text{i}}$ 와 $t_{\text{i}}$ 값 집합이 획득된다. 데이터가 승인되기 전에 2 μV 이내의 일관성을 위해 $V_{\text{null}}$ 의 연속적인 세 값이 검사된다. 이는 양자 전압 스텝 간에 자발적인 전환이 발생할 때 발생할 수 있는 과도 상태에 의해 손상될 수 있는 데이터를 제거한다. 스텝 전환 중에 $V_{\text{a}}$ 와 $V_{\text{null}}$ 이 동일하게 변하므로 $V_{\text{i}}$ 는 일정하게 유지되어 데이터 수집 과정이 스텝 전환에 상대적으로 면역이 된다. 분당 최대 5번의 전환을 일으킬 수 있는 조지프슨 배열 칩의 경우에도 데이터가 효율적으로 수집된다. 미지값과 널 미터의 노이즈로 인한 데이터의 산란은 일반적으로 표준 편차가 20~100 nV 정도인 가우스 프로세스로 모델링될 수 있다. 그러나 이 프로세스에 맞지 않는 간헐적인 노이즈 스파이크가 있으며, 이는 잘 작동하는 데이터에서 1 μV에서 10 μV 떨어진 글리치를 $V_{\text{i}}$ 데이터에 생성한다. 이러한 데이터를 감지하고 제거하기 위해 이상치 테스트가 사용된다.

첫 번째 데이터 세트 수집 후, 미지의 극성이 반전되고( $P=-1$ ), 바이어스가 재조정되어 $V_{\text{null}}$ 을 최소화하는 스텝이 선택되며, 두 번째 데이터 세트가 획득된다. 두 번의 추가 반전을 통해 세 번째 및 네 번째 데이터 세트가 생성된다. $V_{\text{R}},V_{0}$ 및 $m$ 에 대한 최상의 추정치는 네 데이터 세트의 모든 $i$ 에 대해 $V_{\text{i}}-(P_{\text{i}}V_{\text{R}}-V_{0}-mt_{\text{i}})$ 집합의 제곱합 제곱근(RSS) 오차를 최소화하는 최소 제곱 재귀 분석을 통해 얻어진다. 일반적인 제너 표준 측정에서, 표준의 노이즈는 종종 $m$ 의 계산된 값을 지배한다. $V_{\text{R}}$ 에 대한 A형 불확실성은 $V_{\text{i}}$ 집합의 평균의 표준 편차이다. 일반적으로 이 전체 교정 알고리즘은 컴퓨터에 의해 제어되며 몇 분 안에 완료된다. 반전 사이에 불균일한 지연이 있는 데이터를 제외하고, 전체 $V_{\text{i}}$ 세트의 절댓값에 대한 단순 평균은 $V_{\text{z}}$ 의 equally good 추정치이다.

그림 7에 보이는 것과 같은 시스템은 웨스턴 전지, 제너 기준 및 정밀 디지털 전압계와 같은 보조 표준을 교정하는 데 사용된다. 이러한 교정은 조지프슨 배열 전압을 $V=nf/K_{\text{J}}$ 로 설정할 수 있다는 사실에 의해 크게 단순화된다. 여기서 정수 $n$ 은 약 −75000에서 +75000 범위 내의 어떤 값도 가질 수 있다. 10V 제너 표준 측정의 전형적인 불확실성은 제너의 노이즈에 의해 약 0.01 ppm으로 제한된다. 조지프슨 배열을 넓은 범위의 이산 전압으로 설정할 수 있는 능력은 또한 고정밀 디지털 전압계의 선형성을 측정하는 가장 정확한 도구가 되게 한다.

불확실성

조지프슨 소자의 단자 양단에 나타나는 전압은 원칙적으로 $V=nf/K_{\text{J}}$ 로 정확히 주어지지만, 실제 측정에서는 8가지 오차 및 불확실성 원인이 있다.

기준 주파수 오프셋 및 노이즈
누설 전류로 인한 측정 루프의 전압 강하
널 미터 이득 오차, 바이어스 전류, 오프셋, 입력 임피던스, 비선형성 및 노이즈
측정 루프의 보정되지 않은 열 전압
배열 결함에서 기준 주파수 전류의 정류로 인한 오프셋
전자기 간섭의 영향
바이어스 의존성 전압으로 이어지는 결함 있는 접합부 또는 연결
배열의 직렬 저항과 잔류 바이어스 전류의 곱

기준 주파수 오프셋 또는 알려진 누설 저항과 같은 알려진 오차의 경우 보정을 수행할 수 있다. 그런 다음 측정학자의 임무는 보정의 불확실성을 포함하여 모든 불확실성에 현실적인 숫자를 할당하는 것이다. 이를 수행하는 한 가지 방법은 원인 1과 2만이 조지프슨 배열의 전압에 의존한다는 점에 주목한다. 다른 모든 구성 요소는 배열 전압에 관계없이 거의 동일하다. 따라서 원인 3-8의 결합된 효과는 다른 측정에 사용되는 것과 정확히 동일한 알고리즘을 사용하여 단락 회로 측정을 수행함으로써 정량적으로 평가할 수 있다. 원인 3-8로 인한 표준 오차는 단락 회로 측정 세트의 제곱근 평균(RMS) 값이다.^[32] 주파수 및 누설 불확실성을 추정하기 위해 추가 실험을 수행해야 한다. 불확실성을 결합하고 신뢰 구간을 설정하기 위한 국제적으로 승인된 절차는 BIPM의 측정 불확실성 평가 가이드(Guide to the Evaluation of Uncertainty in Measurement)의 주제이다.^[33]

일반적으로 몇 분의 측정 평균화 시간 동안 조지프슨 시스템의 총 불확실성 기여는 몇 나노볼트이다. 이러한 시스템의 가장 일반적인 용도는 50–100 nV의 노이즈 레벨을 가진 제너 표준의 교정이기 때문에 조지프슨 시스템의 기여는 무시할 수 있다.

추적성과 등가성

1904년 의회 법안은 미국의 법적 볼트를 현재 미국 국립표준기술연구소(NIST)가 정의하는 양으로 확립했다. 1990년 볼트의 조지프슨 표현에 대한 국제 협약으로 NIST는 미국의 법적 볼트를 국제 볼트 표현과 동일하게 정의했다. 1984년 첫 조지프슨 배열 전압 표준의 성공 이후, 전 세계 70개 이상의 국가 측정 기관(NMI), 군사 및 상업 연구소로 그 사용이 확산되었다. 이로 인해 원칙적으로 국가 표준만큼 우수한 JVS를 소유한 비NMI의 추적성에 대한 혼란이 발생했다. 이 질문에 대한 일부 지침은 국제 표준화 기구(ISO) 문서에 제공되어 있으며, 이는 NMI와의 비교에 참여한 JVS와 같은 본질적인 표준은 추적성을 주장할 수 있다는 일반 원칙을 명시한다.

같이 보기

도량형학 및 측정 개요

각주

↑ Josephson, B.D. (1962). 《Possible new effects in superconductive tunnelling》. 《Physics Letters》 1 (Elsevier BV). 251–253쪽. Bibcode:1962PhL.....1..251J. doi:10.1016/0031-9163(62)91369-0. ISSN 0031-9163.
↑ Shapiro, Sidney (1963년 7월 15일). 《Josephson Currents in Superconducting Tunneling: The Effect of Microwaves and Other Observations》. 《Physical Review Letters》 11 (American Physical Society (APS)). 80–82쪽. Bibcode:1963PhRvL..11...80S. doi:10.1103/physrevlett.11.80. ISSN 0031-9007.
↑ Parker, W. H.; Langenberg, D. N.; Denenstein, A.; Taylor, B. N. (1969년 1월 10일). 《Determination of ${\frac {e}{h}}$ , Using Macroscopic Quantum Phase Coherence in Superconductors. I. Experiment》. 《Physical Review》 177 (American Physical Society (APS)). 639–664쪽. Bibcode:1969PhRv..177..639P. doi:10.1103/physrev.177.639. ISSN 0031-899X.
↑ Finnegan, T. F.; Denenstein, A.; Langenberg, D. N. (1971년 8월 1일). 《ac-Josephson-Effect Determination of ${\frac {e}{h}}$ : A Standard of Electrochemical Potential Based on Macroscopic Quantum Phase Coherence in Superconductors》. 《Physical Review B》 4 (American Physical Society (APS)). 1487–1522쪽. Bibcode:1971PhRvB...4.1487F. doi:10.1103/physrevb.4.1487. ISSN 0556-2805.
↑ Taylor, B N; Parker, W H; Langenberg, D N; Denenstein, A (1967). 《On the Use of the AC Josephson Effect to Maintain Standards of Electromotive Force》. 《Metrologia》 3 (IOP Publishing). 89–98쪽. Bibcode:1967Metro...3...89T. doi:10.1088/0026-1394/3/4/001. ISSN 0026-1394. S2CID 250802446.
↑ Field, B F; Finnegan, T F; Toots, J (1973). 《Volt Maintenance at NBS via 2e/h: A New Definition of the NBS Volt》. 《Metrologia》 9 (IOP Publishing). 155–166쪽. Bibcode:1973Metro...9..155F. doi:10.1088/0026-1394/9/4/003. ISSN 0026-1394. S2CID 250802287.
↑ Quinn, T J (1988년 12월 1일). 《News from the BIPM》. 《Metrologia》 26 (IOP Publishing). 69–74쪽. doi:10.1088/0026-1394/26/1/006. ISSN 0026-1394. S2CID 250751407.
↑ Fulton, T. A. (1973년 1월 1일). 《Implications of Solid-State Corrections to the Josephson Voltage-Frequency Relation》. 《Physical Review B》 7 (American Physical Society (APS)). 981–982쪽. Bibcode:1973PhRvB...7..981F. doi:10.1103/physrevb.7.981. ISSN 0556-2805.
↑ Tsai, Jaw-Shen; Jain, A. K.; Lukens (1983년 7월 25일). 《High-Precision Test of the Universality of the Josephson Voltage-Frequency Relation》. 《Physical Review Letters》 51 (American Physical Society (APS)). 316–319쪽. Bibcode:1983PhRvL..51..316T. doi:10.1103/physrevlett.51.316. ISSN 0031-9007.
↑ Jain, A. K.; Lukens, J. E.; Tsai, J. -S. (1987년 3월 23일). 《Test for relativistic gravitational effects on charged particlesp》. 《Physical Review Letters》 58 (American Physical Society (APS)). 1165–1168쪽. Bibcode:1987PhRvL..58.1165J. doi:10.1103/physrevlett.58.1165. ISSN 0031-9007. PMID 10034359.
↑
Data taken from the following sources:
- B. W. Petley: in Quantum Metrology and Fundamental Physical Constants, edited by P.H. Cutler and A. A. Lucas (Plenum, New York) 293 (1983)
- Melchert, Friedmund (1979). 《Darstellung der Spannungseinheit mit Hilfe des Josephson-Effektes'》 (독일어). 《Technisches Messen》. 514–524. 59–64쪽. doi:10.1524/teme.1979.514524.jg.59. ISSN 2196-7113. S2CID 111838525.
- Reymann, D.; Witt, T.J. (1993). 《International comparisons of Josephson array voltage standards》. 《IEEE Transactions on Instrumentation and Measurement》 42 (Institute of Electrical and Electronics Engineers (IEEE)). 596–599쪽. Bibcode:1993ITIM...42..596R. doi:10.1109/19.278633. ISSN 0018-9456.
- Lo-Hive, J.P.; Reymann, D.; Geneves, G. (1995). 《Comparisons of 10-V Josephson array voltage standards between the BNM/LCIE and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 44 (Institute of Electrical and Electronics Engineers (IEEE)). 230–233쪽. Bibcode:1995ITIM...44..230L. doi:10.1109/19.377818. ISSN 0018-9456.
- Reymann, D.; Witt, T.J.; Eklund, G.; Pajander, H.; Nilsson, H. (1997). 《Comparison of the Josephson voltage standards of the SP and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 46 (Institute of Electrical and Electronics Engineers (IEEE)). 220–223쪽. Bibcode:1997ITIM...46..220R. doi:10.1109/19.571817. ISSN 0018-9456.
- Reymann, D.; Witt, T.J.; Eklund, G.; Pajander, H.; Nilsson, H.; Behr, R.; Funck, T.; Muller, F. (1999). 《A three-way, on-site comparison of the 10 V Josephson voltage standards of the PTB, the SP, and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 48 (Institute of Electrical and Electronics Engineers (IEEE)). 257–261쪽. Bibcode:1999ITIM...48..257R. doi:10.1109/19.769577. ISSN 0018-9456.
- J. Niemeyer in Handbook of Applied Superconductivity, ed. Bernd Seeber, (Inst. Of Physics Publishing, Philadelphia), 2 p. 1813 (1998)
↑ Endo, Tadashi; Koyanagi, Masao; Nakamura, Akira (1983). 《High-Accuracy Josephson Potentiometer》. 《IEEE Transactions on Instrumentation and Measurement》 32 (Institute of Electrical and Electronics Engineers (IEEE)). 267–271쪽. Bibcode:1983ITIM...32..267E. doi:10.1109/tim.1983.4315056. ISSN 0018-9456. S2CID 46015031.
↑ Levinsen, M. T.; Chiao, R. Y.; Feldman, M. J.; Tucker, B. A. (1977). 《An inverse ac Josephson effect voltage standard》. 《Applied Physics Letters》 31 (AIP Publishing). 776–778쪽. Bibcode:1977ApPhL..31..776L. doi:10.1063/1.89520. ISSN 0003-6951.
↑ Kautz, R. L. (1980). 《On a proposed Josephson‐effect voltage standard at zero current bias》. 《Applied Physics Letters》 36 (AIP Publishing). 386–388쪽. Bibcode:1980ApPhL..36..386K. doi:10.1063/1.91497. ISSN 0003-6951.
↑ Kautz, R.; Costabile, G. (1981). 《A Josephson voltage standard using a series array of 100 junctions》. 《IEEE Transactions on Magnetics》 17 (Institute of Electrical and Electronics Engineers (IEEE)). 780–783쪽. Bibcode:1981ITM....17..780K. doi:10.1109/tmag.1981.1060950. ISSN 0018-9464.
↑ Niemeyer, Jurgen; Hinken, Johann H.; Meier, Wolfgang (1984). 《Microwave-Induced Constant Voltage Steps at Series Arrays of Josephson Tunnel Junctions with Near-Zero Current Bias》. 《IEEE Transactions on Instrumentation and Measurement》 33 (Institute of Electrical and Electronics Engineers (IEEE)). 311–315쪽. Bibcode:1984ITIM...33..311N. doi:10.1109/tim.1984.4315230. ISSN 0018-9456. S2CID 8146756.
↑ Niemeyer, Jurgen; Hinken, Johann H.; Kautz, Richard L. (1985). 《Near-Zero Bias Arrays of Josephson Tunnel Junctions Providing Standard Voltages up to 1 V》. 《IEEE Transactions on Instrumentation and Measurement》. IM-34. 185–187쪽. Bibcode:1985ITIM...34..185N. doi:10.1109/TIM.1985.4315297. ISSN 0018-9456. S2CID 27039645.
↑ Hamilton, C.A.; Kautz, R.L.; Steiner, R.L.; Lloyd, F.L. (1985). 《A practical Josephson voltage standard at 1 V》. 《IEEE Electron Device Letters》 6 (Institute of Electrical and Electronics Engineers (IEEE)). 623–625쪽. Bibcode:1985IEDL....6..623H. doi:10.1109/edl.1985.26253. ISSN 0741-3106. S2CID 19200552.
↑ Niemeyer, J.; Grimm, L.; Meier, W.; Hinken, J. H.; Vollmer, E. (1985). 《Stable Josephson reference voltages between 0.1 and 1.3 V for high‐precision voltage standards》. 《Applied Physics Letters》 47 (AIP Publishing). 1222–1223쪽. Bibcode:1985ApPhL..47.1222N. doi:10.1063/1.96335. ISSN 0003-6951.
↑ IBM J. Res. and Dev. 24 105 (1980)
↑ Lloyd, F.L.; Hamilton, C.A.; Beall, J.A.; Go, D.; Ono, R.H.; Harris, R.E. (1987). 《A Josephson array voltage standard at 10 V》. 《IEEE Electron Device Letters》 8 (Institute of Electrical and Electronics Engineers (IEEE)). 449쪽. Bibcode:1987IEDL....8..449L. doi:10.1109/EDL.1987.26690. S2CID 26398773.
↑ Pöpel, R (1991년 12월 1일). 《The Josephson Effect and Voltage Standards》. 《Metrologia》 29 (IOP Publishing). 153–174쪽. doi:10.1088/0026-1394/29/2/005. ISSN 0026-1394. S2CID 250875516.
↑ Reymann, D.; Witt, T.J. (1993). 《International comparisons of Josephson array voltage standards》. 《IEEE Transactions on Instrumentation and Measurement》 42 (Institute of Electrical and Electronics Engineers (IEEE)). 596–599쪽. Bibcode:1993ITIM...42..596R. doi:10.1109/19.278633. ISSN 0018-9456.
↑ Lo-Hive, J.P.; Reymann, D.; Geneves, G. (1995). 《Comparisons of 10-V Josephson array voltage standards between the BNM/LCIE and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 44 (Institute of Electrical and Electronics Engineers (IEEE)). 230–233쪽. Bibcode:1995ITIM...44..230L. doi:10.1109/19.377818. ISSN 0018-9456.
↑ Kautz, R. L. (1994). 《Quasipotential and the stability of phase lock in nonhysteretic Josephson junctions》. 《Journal of Applied Physics》 76 (AIP Publishing). 5538–5544쪽. Bibcode:1994JAP....76.5538K. doi:10.1063/1.357156. ISSN 0021-8979.
↑ Kautz, R L (1996년 7월 1일). 《Noise, chaos, and the Josephson voltage standard》. 《Reports on Progress in Physics》 59 (IOP Publishing). 935–992쪽. Bibcode:1996RPPh...59..935K. doi:10.1088/0034-4885/59/8/001. ISSN 0034-4885. S2CID 250876976.
↑ Müller, F.; Köhler, H.-J.; Weber, P.; Blüthner, K.; Meyer, H.-G. (December 1990). 《A 1‐V series‐array Josephson voltage standard operated at 35 GHz》. 《J. Appl. Phys.》 68. 4700–4702쪽. Bibcode:1990JAP....68.4700M. doi:10.1063/1.346149.
↑ Hamilton, Clark A.; Kautz, Richard L.; Stieg, Marilyn; Chieh, Kao; Avrin, William F.; Simmonds, Michael B. (May 1991). 《A 24-GHz Josephson array voltage standard》. 《IEEE Transactions on Instrumentation and Measurement》 40. 301–304쪽. Bibcode:1991ITIM...40..301H. doi:10.1109/TIM.1990.1032944.
↑ Müller, F.; Pöpel, R.; Kohlmann, J.; Niemeyer, J.; Meier, W.; Weimann, T.; Grimm, L.; Dünschede, F.-W.; Gutmann, P. (1997). 《Optimized 1 V and 10 V Josephson series arrays》. 《IEEE Transactions on Instrumentation and Measurement》 46 (Institute of Electrical and Electronics Engineers (IEEE)). 229–232쪽. Bibcode:1997ITIM...46..229M. doi:10.1109/19.571819. ISSN 0018-9456.
↑ R. L. Kautz, in Metrology at the Frontiers of Physics and Technology, ed. L. Grovini and T. J. Quinn (Amsterdam: North-Holland) 259 (1992)
↑ Hamilton, Clark A.; Kautz, Richard L.; Lloyd, Frances L.; Steiner, Richard L.; Field, Bruce F. (1987). 《The NBS Josephson array voltage standard》. 《IEEE Transactions on Instrumentation and Measurement》. IM-36. 258–261쪽. Bibcode:1987ITIM...36..258H. doi:10.1109/TIM.1987.6312681. ISSN 0018-9456. S2CID 1711881.
↑ Hamilton, C A; Tang, Y H (1999). 《Evaluating the uncertainty of Josephson voltage standards》. 《Metrologia》 36 (IOP Publishing). 53–58쪽. Bibcode:1999Metro..36...53H. doi:10.1088/0026-1394/36/1/9. ISSN 0026-1394. S2CID 250818769.
↑ Guide to the Expression of Uncertainty in Measurement, Geneva, International Organization for Standardization (1995)

[1] Josephson, B.D. (1962). 《Possible new effects in superconductive tunnelling》. 《Physics Letters》 1 (Elsevier BV). 251–253쪽. Bibcode:1962PhL.....1..251J. doi:10.1016/0031-9163(62)91369-0. ISSN 0031-9163.

[2] Shapiro, Sidney (1963년 7월 15일). 《Josephson Currents in Superconducting Tunneling: The Effect of Microwaves and Other Observations》. 《Physical Review Letters》 11 (American Physical Society (APS)). 80–82쪽. Bibcode:1963PhRvL..11...80S. doi:10.1103/physrevlett.11.80. ISSN 0031-9007.

[3] Parker, W. H.; Langenberg, D. N.; Denenstein, A.; Taylor, B. N. (1969년 1월 10일). 《Determination of ${\frac {e}{h}}$ , Using Macroscopic Quantum Phase Coherence in Superconductors. I. Experiment》. 《Physical Review》 177 (American Physical Society (APS)). 639–664쪽. Bibcode:1969PhRv..177..639P. doi:10.1103/physrev.177.639. ISSN 0031-899X.

[4] Finnegan, T. F.; Denenstein, A.; Langenberg, D. N. (1971년 8월 1일). 《ac-Josephson-Effect Determination of ${\frac {e}{h}}$ : A Standard of Electrochemical Potential Based on Macroscopic Quantum Phase Coherence in Superconductors》. 《Physical Review B》 4 (American Physical Society (APS)). 1487–1522쪽. Bibcode:1971PhRvB...4.1487F. doi:10.1103/physrevb.4.1487. ISSN 0556-2805.

[5] Taylor, B N; Parker, W H; Langenberg, D N; Denenstein, A (1967). 《On the Use of the AC Josephson Effect to Maintain Standards of Electromotive Force》. 《Metrologia》 3 (IOP Publishing). 89–98쪽. Bibcode:1967Metro...3...89T. doi:10.1088/0026-1394/3/4/001. ISSN 0026-1394. S2CID 250802446.

[6] Field, B F; Finnegan, T F; Toots, J (1973). 《Volt Maintenance at NBS via 2e/h: A New Definition of the NBS Volt》. 《Metrologia》 9 (IOP Publishing). 155–166쪽. Bibcode:1973Metro...9..155F. doi:10.1088/0026-1394/9/4/003. ISSN 0026-1394. S2CID 250802287.

[7] Quinn, T J (1988년 12월 1일). 《News from the BIPM》. 《Metrologia》 26 (IOP Publishing). 69–74쪽. doi:10.1088/0026-1394/26/1/006. ISSN 0026-1394. S2CID 250751407.

[8] Fulton, T. A. (1973년 1월 1일). 《Implications of Solid-State Corrections to the Josephson Voltage-Frequency Relation》. 《Physical Review B》 7 (American Physical Society (APS)). 981–982쪽. Bibcode:1973PhRvB...7..981F. doi:10.1103/physrevb.7.981. ISSN 0556-2805.

[9] Tsai, Jaw-Shen; Jain, A. K.; Lukens (1983년 7월 25일). 《High-Precision Test of the Universality of the Josephson Voltage-Frequency Relation》. 《Physical Review Letters》 51 (American Physical Society (APS)). 316–319쪽. Bibcode:1983PhRvL..51..316T. doi:10.1103/physrevlett.51.316. ISSN 0031-9007.

[10] Jain, A. K.; Lukens, J. E.; Tsai, J. -S. (1987년 3월 23일). 《Test for relativistic gravitational effects on charged particlesp》. 《Physical Review Letters》 58 (American Physical Society (APS)). 1165–1168쪽. Bibcode:1987PhRvL..58.1165J. doi:10.1103/physrevlett.58.1165. ISSN 0031-9007. PMID 10034359.

[11] Data taken from the following sources:
B. W. Petley: in Quantum Metrology and Fundamental Physical Constants, edited by P.H. Cutler and A. A. Lucas (Plenum, New York) 293 (1983)

Melchert, Friedmund (1979). 《Darstellung der Spannungseinheit mit Hilfe des Josephson-Effektes'》 (독일어). 《Technisches Messen》. 514–524. 59–64쪽. doi:10.1524/teme.1979.514524.jg.59. ISSN 2196-7113. S2CID 111838525.

Reymann, D.; Witt, T.J. (1993). 《International comparisons of Josephson array voltage standards》. 《IEEE Transactions on Instrumentation and Measurement》 42 (Institute of Electrical and Electronics Engineers (IEEE)). 596–599쪽. Bibcode:1993ITIM...42..596R. doi:10.1109/19.278633. ISSN 0018-9456.

Lo-Hive, J.P.; Reymann, D.; Geneves, G. (1995). 《Comparisons of 10-V Josephson array voltage standards between the BNM/LCIE and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 44 (Institute of Electrical and Electronics Engineers (IEEE)). 230–233쪽. Bibcode:1995ITIM...44..230L. doi:10.1109/19.377818. ISSN 0018-9456.

Reymann, D.; Witt, T.J.; Eklund, G.; Pajander, H.; Nilsson, H. (1997). 《Comparison of the Josephson voltage standards of the SP and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 46 (Institute of Electrical and Electronics Engineers (IEEE)). 220–223쪽. Bibcode:1997ITIM...46..220R. doi:10.1109/19.571817. ISSN 0018-9456.

Reymann, D.; Witt, T.J.; Eklund, G.; Pajander, H.; Nilsson, H.; Behr, R.; Funck, T.; Muller, F. (1999). 《A three-way, on-site comparison of the 10 V Josephson voltage standards of the PTB, the SP, and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 48 (Institute of Electrical and Electronics Engineers (IEEE)). 257–261쪽. Bibcode:1999ITIM...48..257R. doi:10.1109/19.769577. ISSN 0018-9456.

J. Niemeyer in Handbook of Applied Superconductivity, ed. Bernd Seeber, (Inst. Of Physics Publishing, Philadelphia), 2 p. 1813 (1998)

[12] B. W. Petley: in Quantum Metrology and Fundamental Physical Constants, edited by P.H. Cutler and A. A. Lucas (Plenum, New York) 293 (1983)

[13] Melchert, Friedmund (1979). 《Darstellung der Spannungseinheit mit Hilfe des Josephson-Effektes'》 (독일어). 《Technisches Messen》. 514–524. 59–64쪽. doi:10.1524/teme.1979.514524.jg.59. ISSN 2196-7113. S2CID 111838525.

[14] Reymann, D.; Witt, T.J. (1993). 《International comparisons of Josephson array voltage standards》. 《IEEE Transactions on Instrumentation and Measurement》 42 (Institute of Electrical and Electronics Engineers (IEEE)). 596–599쪽. Bibcode:1993ITIM...42..596R. doi:10.1109/19.278633. ISSN 0018-9456.

[15] Lo-Hive, J.P.; Reymann, D.; Geneves, G. (1995). 《Comparisons of 10-V Josephson array voltage standards between the BNM/LCIE and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 44 (Institute of Electrical and Electronics Engineers (IEEE)). 230–233쪽. Bibcode:1995ITIM...44..230L. doi:10.1109/19.377818. ISSN 0018-9456.

[16] Reymann, D.; Witt, T.J.; Eklund, G.; Pajander, H.; Nilsson, H. (1997). 《Comparison of the Josephson voltage standards of the SP and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 46 (Institute of Electrical and Electronics Engineers (IEEE)). 220–223쪽. Bibcode:1997ITIM...46..220R. doi:10.1109/19.571817. ISSN 0018-9456.

[17] Reymann, D.; Witt, T.J.; Eklund, G.; Pajander, H.; Nilsson, H.; Behr, R.; Funck, T.; Muller, F. (1999). 《A three-way, on-site comparison of the 10 V Josephson voltage standards of the PTB, the SP, and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 48 (Institute of Electrical and Electronics Engineers (IEEE)). 257–261쪽. Bibcode:1999ITIM...48..257R. doi:10.1109/19.769577. ISSN 0018-9456.

[18] J. Niemeyer in Handbook of Applied Superconductivity, ed. Bernd Seeber, (Inst. Of Physics Publishing, Philadelphia), 2 p. 1813 (1998)

[12] Endo, Tadashi; Koyanagi, Masao; Nakamura, Akira (1983). 《High-Accuracy Josephson Potentiometer》. 《IEEE Transactions on Instrumentation and Measurement》 32 (Institute of Electrical and Electronics Engineers (IEEE)). 267–271쪽. Bibcode:1983ITIM...32..267E. doi:10.1109/tim.1983.4315056. ISSN 0018-9456. S2CID 46015031.

[13] Levinsen, M. T.; Chiao, R. Y.; Feldman, M. J.; Tucker, B. A. (1977). 《An inverse ac Josephson effect voltage standard》. 《Applied Physics Letters》 31 (AIP Publishing). 776–778쪽. Bibcode:1977ApPhL..31..776L. doi:10.1063/1.89520. ISSN 0003-6951.

[14] Kautz, R. L. (1980). 《On a proposed Josephson‐effect voltage standard at zero current bias》. 《Applied Physics Letters》 36 (AIP Publishing). 386–388쪽. Bibcode:1980ApPhL..36..386K. doi:10.1063/1.91497. ISSN 0003-6951.

[15] Kautz, R.; Costabile, G. (1981). 《A Josephson voltage standard using a series array of 100 junctions》. 《IEEE Transactions on Magnetics》 17 (Institute of Electrical and Electronics Engineers (IEEE)). 780–783쪽. Bibcode:1981ITM....17..780K. doi:10.1109/tmag.1981.1060950. ISSN 0018-9464.

[16] Niemeyer, Jurgen; Hinken, Johann H.; Meier, Wolfgang (1984). 《Microwave-Induced Constant Voltage Steps at Series Arrays of Josephson Tunnel Junctions with Near-Zero Current Bias》. 《IEEE Transactions on Instrumentation and Measurement》 33 (Institute of Electrical and Electronics Engineers (IEEE)). 311–315쪽. Bibcode:1984ITIM...33..311N. doi:10.1109/tim.1984.4315230. ISSN 0018-9456. S2CID 8146756.

[17] Niemeyer, Jurgen; Hinken, Johann H.; Kautz, Richard L. (1985). 《Near-Zero Bias Arrays of Josephson Tunnel Junctions Providing Standard Voltages up to 1 V》. 《IEEE Transactions on Instrumentation and Measurement》. IM-34. 185–187쪽. Bibcode:1985ITIM...34..185N. doi:10.1109/TIM.1985.4315297. ISSN 0018-9456. S2CID 27039645.

[18] Hamilton, C.A.; Kautz, R.L.; Steiner, R.L.; Lloyd, F.L. (1985). 《A practical Josephson voltage standard at 1 V》. 《IEEE Electron Device Letters》 6 (Institute of Electrical and Electronics Engineers (IEEE)). 623–625쪽. Bibcode:1985IEDL....6..623H. doi:10.1109/edl.1985.26253. ISSN 0741-3106. S2CID 19200552.

[19] Niemeyer, J.; Grimm, L.; Meier, W.; Hinken, J. H.; Vollmer, E. (1985). 《Stable Josephson reference voltages between 0.1 and 1.3 V for high‐precision voltage standards》. 《Applied Physics Letters》 47 (AIP Publishing). 1222–1223쪽. Bibcode:1985ApPhL..47.1222N. doi:10.1063/1.96335. ISSN 0003-6951.

[20] IBM J. Res. and Dev. 24 105 (1980)

[21] Lloyd, F.L.; Hamilton, C.A.; Beall, J.A.; Go, D.; Ono, R.H.; Harris, R.E. (1987). 《A Josephson array voltage standard at 10 V》. 《IEEE Electron Device Letters》 8 (Institute of Electrical and Electronics Engineers (IEEE)). 449쪽. Bibcode:1987IEDL....8..449L. doi:10.1109/EDL.1987.26690. S2CID 26398773.

[22] Pöpel, R (1991년 12월 1일). 《The Josephson Effect and Voltage Standards》. 《Metrologia》 29 (IOP Publishing). 153–174쪽. doi:10.1088/0026-1394/29/2/005. ISSN 0026-1394. S2CID 250875516.

[23] Reymann, D.; Witt, T.J. (1993). 《International comparisons of Josephson array voltage standards》. 《IEEE Transactions on Instrumentation and Measurement》 42 (Institute of Electrical and Electronics Engineers (IEEE)). 596–599쪽. Bibcode:1993ITIM...42..596R. doi:10.1109/19.278633. ISSN 0018-9456.

[24] Lo-Hive, J.P.; Reymann, D.; Geneves, G. (1995). 《Comparisons of 10-V Josephson array voltage standards between the BNM/LCIE and the BIPM》. 《IEEE Transactions on Instrumentation and Measurement》 44 (Institute of Electrical and Electronics Engineers (IEEE)). 230–233쪽. Bibcode:1995ITIM...44..230L. doi:10.1109/19.377818. ISSN 0018-9456.

[25] Kautz, R. L. (1994). 《Quasipotential and the stability of phase lock in nonhysteretic Josephson junctions》. 《Journal of Applied Physics》 76 (AIP Publishing). 5538–5544쪽. Bibcode:1994JAP....76.5538K. doi:10.1063/1.357156. ISSN 0021-8979.

[26] Kautz, R L (1996년 7월 1일). 《Noise, chaos, and the Josephson voltage standard》. 《Reports on Progress in Physics》 59 (IOP Publishing). 935–992쪽. Bibcode:1996RPPh...59..935K. doi:10.1088/0034-4885/59/8/001. ISSN 0034-4885. S2CID 250876976.

[27] Müller, F.; Köhler, H.-J.; Weber, P.; Blüthner, K.; Meyer, H.-G. (December 1990). 《A 1‐V series‐array Josephson voltage standard operated at 35 GHz》. 《J. Appl. Phys.》 68. 4700–4702쪽. Bibcode:1990JAP....68.4700M. doi:10.1063/1.346149.

[28] Hamilton, Clark A.; Kautz, Richard L.; Stieg, Marilyn; Chieh, Kao; Avrin, William F.; Simmonds, Michael B. (May 1991). 《A 24-GHz Josephson array voltage standard》. 《IEEE Transactions on Instrumentation and Measurement》 40. 301–304쪽. Bibcode:1991ITIM...40..301H. doi:10.1109/TIM.1990.1032944.

[29] Müller, F.; Pöpel, R.; Kohlmann, J.; Niemeyer, J.; Meier, W.; Weimann, T.; Grimm, L.; Dünschede, F.-W.; Gutmann, P. (1997). 《Optimized 1 V and 10 V Josephson series arrays》. 《IEEE Transactions on Instrumentation and Measurement》 46 (Institute of Electrical and Electronics Engineers (IEEE)). 229–232쪽. Bibcode:1997ITIM...46..229M. doi:10.1109/19.571819. ISSN 0018-9456.

[30] R. L. Kautz, in Metrology at the Frontiers of Physics and Technology, ed. L. Grovini and T. J. Quinn (Amsterdam: North-Holland) 259 (1992)

[31] Hamilton, Clark A.; Kautz, Richard L.; Lloyd, Frances L.; Steiner, Richard L.; Field, Bruce F. (1987). 《The NBS Josephson array voltage standard》. 《IEEE Transactions on Instrumentation and Measurement》. IM-36. 258–261쪽. Bibcode:1987ITIM...36..258H. doi:10.1109/TIM.1987.6312681. ISSN 0018-9456. S2CID 1711881.

[32] Hamilton, C A; Tang, Y H (1999). 《Evaluating the uncertainty of Josephson voltage standards》. 《Metrologia》 36 (IOP Publishing). 53–58쪽. Bibcode:1999Metro..36...53H. doi:10.1088/0026-1394/36/1/9. ISSN 0026-1394. S2CID 250818769.

[33] Guide to the Expression of Uncertainty in Measurement, Geneva, International Organization for Standardization (1995)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]