퍼넷 사각형


퍼넷 사각형 또는 퍼넷 스퀘어(Punnett square)는 특정 교배 또는 번식 실험의 유전자형을 예측하는 데 사용되는 사각형 다이어그램이다. 1905년에 이 방법을 고안한 레지널드 퍼넷의 이름을 따서 명명되었다.[3][4][5][6][7][8] 이 다이어그램은 생물학자들이 자손이 특정 유전자형을 가질 확률을 결정하는 데 사용된다. 퍼넷 사각형은 모계 대립 유전자와 부계 대립 유전자의 가능한 조합을 표로 요약한 것이다.[9] 이 표는 단일 형질(대립 유전자)의 자손 유전자형 결과 확률을 조사하거나, 부모로부터 여러 형질을 교배할 때 사용될 수 있다.
퍼넷 사각형은 그레고어 멘델이 발견한 유전학의 기본 개념인 멘델의 유전법칙을 시각적으로 나타낸다.[10] 여러 형질의 경우, "분기선 방법"을 사용하는 것이 퍼넷 사각형보다 일반적으로 훨씬 쉽다. 표현형은 퍼넷 사각형을 사용하여 우연보다 나은 정확도로 예측될 수 있지만, 주어진 유전자형이 있을 때 나타날 수 있는 표현형은 때때로 다가 유전 및 후성유전학과 같이 다른 여러 요인의 영향을 받을 수 있다.
접합성
[편집]접합성은 생물에서 특정 형질을 결정하는 대립 유전자 간의 유사성 정도를 나타낸다. 가장 간단한 형태로, 한 쌍의 대립 유전자는 동형접합 또는 이형접합일 수 있다. 동형접합은 동형(homo)이 같음을, 접합(zygous)이 수정란을 의미하며, 두 우성 또는 두 열성 대립 유전자의 조합이 동일한 형질을 암호화할 때 나타난다. 열성은 항상 소문자로 표기한다. 예를 들어, 각 대립 유전자의 대표 문자로 'A'를 사용하면, 동형 우성 쌍의 유전자형은 'AA'로, 동형 열성은 'aa'로 표시된다. 이형접합은 이형(hetero)이 다름과 관련되며, 'Aa'만 가능하다 (관례상 대문자가 항상 먼저 표시된다). 동형 우성 쌍의 표현형은 'A', 즉 우성이며, 동형 열성의 경우는 그 반대이다. 이형접합 쌍은 항상 우성 표현형을 갖는다.[11] 더 작은 정도로 반접합성[12]과 무접합성[13]도 유전자 쌍에서 볼 수 있다.
단일 인자 교배
[편집]"단일-"은 "하나"를 의미한다. 이 교배는 단일 형질에 대한 조사를 나타낸다. 예를 들어 눈 색깔이 될 수 있다. 각 유전자 자리(locus)는 항상 두 글자로 표현된다. 따라서 눈 색깔의 경우 "B = 갈색 눈"이고 "b = 녹색 눈"이라고 하자. 이 예에서 두 부모는 유전자형 Bb를 갖는다. 눈 색깔의 예에서는 둘 다 갈색 눈을 가졌음을 의미한다. 그들은 B 또는 b 대립 유전자를 포함하는 생식자를 생산할 수 있다. (유전학에서는 우성 대립 유전자를 나타내기 위해 대문자를 사용하고 열성 대립 유전자를 나타내기 위해 소문자를 사용하는 것이 관례이다.) 개별 자손이 유전자형 BB를 가질 확률은 25%, Bb는 50%, bb는 25%이다. 표현형의 비율은 3:1이며, 이는 단일 인자 교배의 전형적인 결과이다. 이로부터 표현형을 평가할 때, 자손 중 "3"은 "갈색" 눈을 가지고 오직 한 자손만 "녹색" 눈을 가진다. (3은 "B?"이고 1은 "bb"이다.)
부계 모계 |
B | b |
|---|---|---|
| B | BB | Bb |
| b | Bb | bb |
B와 b 대립 유전자들이 자손의 외모에 영향을 주기 위해 서로 상호작용하는 방식은 유전자 산물(단백질)이 상호작용하는 방식에 따라 달라진다 (멘델의 유전법칙 참조). 여기에는 치명적인 효과와 상위성(하나의 대립 유전자가 우성 또는 열성 여부와 관계없이 다른 대립 유전자를 가리는 현상)이 포함될 수 있다.
이중 인자 교배
[편집]두 개 이상의 유전자를 살펴보면 더 복잡한 교배를 만들 수 있다. 그러나 퍼넷 사각형은 유전자들이 서로 독립적인 경우에만 작동한다. 이는 유전자 "A"의 특정 대립 유전자를 가지고 있는 것이 유전자 "B"의 대립 유전자를 소유할 확률을 바꾸지 않는다는 것을 의미한다. 이는 유전자들이 연관되어 있지 않아, 감수 분열 동안 두 유전자가 함께 분리되는 경향이 없음을 나타내는 것과 같다.
다음 예시는 두 이형접합 완두콩 식물 사이의 이중 인자 교배를 보여준다. R은 모양(둥근)에 대한 우성 대립 유전자를 나타내고, r은 열성 대립 유전자(주름진)를 나타낸다. A는 색깔(노란색)에 대한 우성 대립 유전자를 나타내고, a는 열성 대립 유전자(녹색)를 나타낸다. 각 식물이 유전자형 RrAa를 가지고 있고, 모양 및 색깔 유전자에 대한 대립 유전자들이 독립적이라면, 그들은 가능한 모든 조합을 가진 네 가지 유형의 생식자: RA, Ra, rA, ra를 생산할 수 있다.
| RA | Ra | rA | ra | |
|---|---|---|---|---|
| RA | RRAA | RRAa | RrAA | RrAa |
| Ra | RRAa | RRaa | RrAa | Rraa |
| rA | RrAA | RrAa | rrAA | rrAa |
| ra | RrAa | Rraa | rrAa | rraa |
우성 형질이 열성 형질을 가리므로(상위성이 없다고 가정), 둥근 노란색 표현형을 갖는 조합이 9가지, 둥근 녹색이 3가지, 주름진 노란색이 3가지, 주름진 녹색이 1가지이다. 9:3:3:1의 비율은 연관되지 않은 유전자를 가진 두 이형접합 부모를 교배할 때 예상되는 결과이다. 다른 비율은 다른 어떤 일이 일어났음을 나타낸다(예: 치사 대립 유전자, 상위성, 연관 유전자 등).
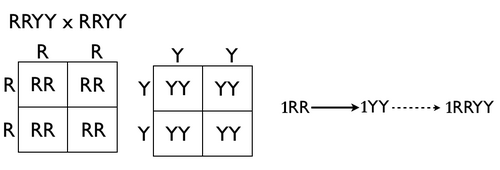
분기선 방법
[편집]분기선 방법(트리 방법 및 가지치기 시스템으로도 알려짐)은 이중 인자 및 다중 인자 교배를 해결할 수도 있다. 문제는 일련의 단일 인자 교배로 전환되고, 결과는 트리에서 결합된다. 그러나 트리는 퍼넷 사각형보다 적은 시간과 더 명확하게 동일한 결과를 생성한다. 아래 예시는 RrYy x RrYy를 사용하여 또 다른 이중 이형접합 교배를 평가한다. 위에서 언급했듯이, 연관되지 않은 유전자를 가진 두 이중 이형접합체를 교배할 경우 표현형 비율은 9:3:3:1이 될 것으로 예상된다. 유전자형 비율은 아래 다이어그램에서 얻어졌으며, 이 다이어그램은 표현형 비율만 분석할 때보다 더 많은 가지를 가질 것이다.

같이 보기
[편집]각주
[편집]- ↑ Mendel, Gregor Johann (1866). 《Versuche über Pflanzen-Hybriden》. 《BSHS Translations》. Verhandlungen des naturforschenden Vereins (독일어, 영어) IV Separate판 (Brno: Verlag des naturforschender Vereins zu Brünn / Georg Gastl's Buchdruckerei /). p. 14. 2021년 3월 29일에 원본 문서에서 보존된 문서. 2020년 6월 1일에 확인함.
- ↑ Mendel, Gregor Johann (1866). 《Versuche über Pflanzen-Hybriden》. 《BSHS Translations》. Verhandlungen des naturforschenden Vereins (독일어, 영어) IV Separate판 (Brno: Verlag des naturforschender Vereins zu Brünn / Georg Gastl's Buchdruckerei). p. 47. 2021년 3월 29일에 원본 문서에서 보존된 문서. 2020년 6월 1일에 확인함.
- ↑ Punnett, Reginald Crundall (1907). 《Mendelism》 2판. London, UK: Macmillan. (NB. The 1905 first edition of this book does not contain the Punnett square. In 1911, the third edition gives a more thorough explanation.)
- ↑ Edwards, Anthony William Fairbank (March 2012). 《Punnett's square》. 《Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences》 43. 219–224. doi:10.1016/j.shpsc.2011.11.011. PMID 22326091.
The origin and development of Punnett's Square for the enumeration and display of genotypes arising in a cross in Mendelian genetics is described. Due to R. C. Punnett, the idea evolved through the work of the 'Cambridge geneticists', including Punnett's colleagues William Bateson, E. R. Saunders and R. H. Lock, soon after the rediscovery of Mendel's paper in 1900. These geneticists were thoroughly familiar with Mendel's paper, which itself contained a similar square diagram. A previously-unpublished three-factor diagram by Sir Francis Galton existing in the Bateson correspondence in Cambridge University Library is then described. Finally the connection between Punnett's Square and Venn Diagrams is emphasized, and it is pointed out that Punnett, Lock and John Venn overlapped as Fellows of Gonville and Caius College, Cambridge.
- ↑ Edwards, Anthony William Fairbank (September 2012). 《Reginald Crundall Punnett: First Arthur Balfour Professor of Genetics, Cambridge, 1912》. Perspectives. 《Genetics》 192 (Gonville and Caius College, Cambridge, UK: Genetics Society of America). 3–13쪽. doi:10.1534/genetics.112.143552. PMC 3430543. PMID 22964834.
[...] Punnett's square seems to have been a development of 1905, too late for the first edition of his Mendelism (May 1905) but much in evidence in Report III to the Evolution Committee of the Royal Society [(Bateson et al. 1906b) "received March 16, 1906"]. The earliest mention is contained in a letter to Bateson from Francis Galton dated October 1, 1905 (Edwards 2012). We have the testimony of Bateson (1909, p. 57) that "For the introduction of this system [the 'graphic method'], which greatly simplifies difficult cases, I am indebted to Mr. Punnett." [...] The first published diagrams appeared in 1906. [...] when Punnett published the second edition of his Mendelism, he used a slightly different format ([...] Punnett 1907, p. 45) [...] In the third edition (Punnett 1911, p. 34) he reverted to the arrangement [...] with a description of the construction of what he called the "chessboard" method (although in truth it is more like a multiplication table). [...]
(11 pages) - ↑ Wimsatt, William C. (2012년 5월 15일), “The analytic geometry of genetics: Part I: the structure, function, and early evolution of Punnett squares”, 《Archive for History of Exact Sciences》 66 (66): 359–396 [359], doi:10.1007/s00407-012-0096-7, S2CID 119557681
- ↑ Edwards, Anthony William Fairbank (June 2016). 《Punnett's square: a postscript》. 《Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences》 57 (Elsevier Ltd.). 69–70쪽. doi:10.1016/j.shpsc.2016.01.001. 2021년 3월 29일에 확인함. (2 pages)
- ↑ Müller-Wille, Staffan; Parolini, Giuditta (2020년 12월 9일). 〈Punnett squares and hybrid crosses: how Mendelians learned their trade by the book〉. 《Learning by the Book: Manuals and Handbooks in the History of Science》. BJHS Themes 5. British Society for the History of Science / Cambridge University Press. 149–165쪽. doi:10.1017/bjt.2020.12. S2CID 229344415. 2021년 3월 29일에 원본 문서에서 보존된 문서. 2021년 3월 29일에 확인함.
[...] Nilsson-Ehle was experimenting with a visual arrangement that would become very popular in Mendelian genetics. The lower half of his notes comes close to what is known as the 'Punnett square' [...] Punnett introduced this square diagram to the literature in 1906 in a paper co-authored with Bateson and Edith R. Saunders, and included it in the second edition of his Mendelism. In the third edition (1911), he added a verbal description of how to construct the diagram, and the Punnett square became a standard feature of Mendelian literature. As a detailed reconstruction by A.W.F. Edwards has shown, the diagram first took shape in an exchange of letters between Bateson and Galton for the more complex case of a trihybrid cross, and may well have been inspired by the way in which Mendel presented a case of trifactorial inheritance of flower colour in beans. [...]
- ↑ Griffiths, Anthony J. F.; Miller, Jeffrey H.; Suzuki, David T.; Lewontin, Richard C.; Gelbart, William M. (2000). 《An Introduction to Genetic Analysis》 7판. New York, USA: W. H. Freeman.
- ↑ Basu, Arkatappa. “"The Hindu ePaper | Daily News and Current Affairs"”. 《epaper.thehindu.com》 (1 April 2024) (The Hindu). 2024년 3월 13일에 원본 문서에서 보존된 문서. 2024년 4월 1일에 확인함.
- ↑ AthenaMyth (2014년 6월 16일). “Dominant/Recessive vs Hetero/Homozygous”. 《DeviantArt》. 2021년 3월 29일에 원본 문서에서 보존된 문서. 2017년 11월 19일에 확인함.
- ↑ Shiel Jr., William C. (2018년 12월 12일). “Medical Definition of Hemizygous”. 《MedicineNet》. MedicineNet, Inc. 2021년 3월 29일에 원본 문서에서 보존된 문서. 2017년 11월 19일에 확인함.
- ↑ Robles, Ivan Suarez (2010년 11월 16일). “nullizygous”. 《Huntington's Outreach Project for Education, at Stanford (hopes)》. web.stanford.edu. 2021년 3월 29일에 원본 문서에서 보존된 문서. 2017년 11월 19일에 확인함.
더 읽어보기
[편집]- Campbell, Neil Allison (2005). 《Biology》 7판. Benjamin-Cummings Publishing Company. ISBN 978-0-8053-7146-8. OCLC 71890442.