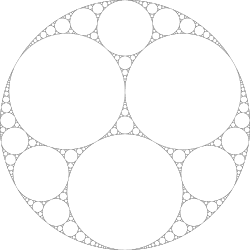
Circle packing theorem

"Coin graph" redirects here. For contact graphs of equal-radius disks, see penny graph.

A circle packing and its graph of tangencies

The circle packing theorem (also known as the Koebe–Andreev–Thurston theorem) describes the possible patterns of tangent circles among non-overlapping circles in the plane. A circle packing is a collection of circles whose union is connected and whose interiors are disjoint. The intersection graph of a circle packing, called a coin graph, is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph: every finite connected simple planar graph $G$ has a circle packing in the plane whose intersection graph is isomorphic to $G$.

A stronger form of the circle packing theorem applies to any polyhedral graph and its dual graph, and proves the existence of a primal–dual packing, circle packings for both graphs that cross at right angles. Circle packings and their tangencies, and the circle packing theorem, have been extended to arbitrary Riemannian surfaces including the sphere, the hyperbolic plane, and to surfaces of bounded genus. More generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. As a special case, the coin graphs of packings of unit circles are called penny graphs.

Circle packings have applications in conformal mapping, the construction of polyhedra, planar separator theorems, graph drawing, and the theory of random walks. The study of the tangencies of circle packings, for which the circle packing theorem is central, should be distinguished from the study of circle packings within fixed shapes but without specified tangencies, typically studied with respect to their density (the fraction of area covered by circles).

Theorem statement and proofs

A maximal planar graph $G$ is a finite simple planar graph to which no more edges can be added while preserving planarity. It may be embedded in the plane with different choices of the outer face, but all such embeddings share the same set of faces (including the outer face) which must all be triangles. The circle packing theorem guarantees the existence of a circle packing with finitely many circles whose intersection graph is isomorphic to $G$. As the following theorem states more formally, every maximal planar graph can have at most one packing.

Koebe–Andreev–Thurston circle packing theorem—If $G$ is a finite connected planar graph, then a circle packing in the plane whose tangency graph is isomorphic to $G$ exists. If $G$ has a fixed planar embedding, the circle packing can be chosen so that the cyclic order of tangencies around each circle corresponds to the order of edges around each vertex in the embedding. If $G$ is maximal planar, this packing is unique, up to reflections in lines and Möbius transformations.

The geometric transformations in the uniqueness part of the theorem, reflections and Möbius transformation, preserve circles, and therefore the tangency graph of any system of circles. Uniqueness means that, for any two packings of the same maximal planar graph, there exists a transformation of these types that takes one packing into the other. For every finite planar graph $G$, it is possible to add vertices to $G$ to construct a larger maximal planar graph in which $G$ is an induced subgraph. Constructing a circle packing from this larger graph, and then removing the circles for the added vertices, produces a circle packing for $G$. This allows the existence of circle packings for arbitrary planar graphs to be derived from the special case for maximal planar graphs.

Existence

Paul Koebe's original proof of the existence of a circle packing for any planar graph is based on his conformal uniformization theorem saying that a finitely connected planar domain is conformally equivalent to a circle domain. A circle domain is a domain, a connected open subset of the plane, whose boundary components are circles or points. It is finitely connected when it has finitely many boundary components, and hence finite first Betti number (the number of generators of its fundamental group). The circle packing is a limiting case of Koebe's result, for domains complementary to the union of disks of the desired circle packing. Koebe conjectured that the finite connectivity assumption was unnecessary in his theorem but was unable to prove it. He & Schramm (1993) extend Koebe's theorem to countably connected domains, and to certain packings of countably many circles.

Thurston's proof is based on the Brouwer fixed point theorem. Another proof uses a discrete variant of Perron's method of constructing solutions to the Dirichlet problem. Yves Colin de Verdière proved the existence of the circle packing as a minimizer of a convex function on a certain configuration space, and Chow & Luo (2003) find another proof using a combinatorial analogue of Ricci flow. As MathSciNet reviewer Igor Rivin writes, this is also the gradient flow of a function that "may well be the one introduced by Colin de Verdière".

Another proof starts with a circle packing with the correct number of disks but an incorrect pattern of tangencies, for which existence is easy to prove, such as an Apollonian packing. It then corrects the tangencies, one at a time, by removing one edge from the corresponding maximal planar graph and replacing it by the other diagonal of the resulting quadrilateral, at the same time adjusting the packing to match this change, in effect walking in a flip graph of triangulations, until reaching the desired graph of tangencies.

Uniqueness

Thurston observes that this uniqueness is a consequence of the Mostow rigidity theorem. To see this, let $G$ be represented by a circle packing. Then the plane in which the circles are packed may be viewed as the boundary of a halfspace model for three-dimensional hyperbolic space; with this view, each circle is the boundary of a plane within the hyperbolic space. One can define a set of disjoint planes in this way from the circles of the packing, and a second set of disjoint planes defined by the circles that circumscribe each triangular gap between three of the circles in the packing. These two sets of planes meet at right angles, and form the generators of a reflection group whose fundamental domain can be viewed as a hyperbolic manifold. By Mostow rigidity, the hyperbolic structure of this domain is uniquely determined, up to isometry of the hyperbolic space; these isometries, when viewed in terms of their actions on the Euclidean plane on the boundary of the half-plane model, translate to Möbius transformations.

Schramm (1991) generalizes the uniqueness of circle packings to certain packings of infinitely many circles on a sphere or open disk. His uniqueness theorem applies to circle packings in which the connected components of the space outside all circles are either circular triangles or individual singular points. The graph of tangencies of such a packing and the triangles determined by the non-singular components form a triangulation of the sphere or disk, punctured at the singular points. Schramm proves that when any two packings have at most a countably infinite set of singularities and have combinatorially equivalent triangulations, they are equivalent under Möbius transformations. This uniqueness argument does not, however, characterize the triangulations for which such a packing exists.

Generalizations

Infinite periodic locally finite circle packing

A Doyle spiral, not locally finite at the spiral center

A version of the circle packing applies to some infinite graphs. In particular, an infinite planar triangulation of an open disk has a locally finite packing in either the Euclidean plane or the hyperbolic plane (but not both). Here, locally finite means that every point of the plane has a neighborhood that intersects only finitely many circles. In the Euclidean case, the packing is unique up to similarity; in the hyperbolic case, it is unique up to isometry.

The circle packing theorem generalizes to graphs that are not planar. If $G$ is a graph that can be embedded on a surface $S$ (more precisely, an orientable 2-manifold), then there is a Riemannian metric of constant curvature $d$ on $S$ and a circle packing on $(S,d)$ whose contact graph is isomorphic to $G$. If $S$ is closed (compact and without boundary) and $G$ is a triangulation of $S$, then $(S,d)$ and the packing are unique up to conformal equivalence. If $S$ is the sphere, then its geometry is spherical geometry and the equivalence is up to Möbius transformations. If it is a torus, the geometry is locally Euclidean (as a flat torus), and the equivalence is up to scaling by a constant and isometries. If $S$ has genus at least 2, then the geometry is locally hyperbolic and the equivalence is up to isometries.

Another generalization of the circle packing theorem involves replacing the condition of tangency with a specified intersection angle between circles corresponding to neighboring vertices. One version is as follows. Suppose that $G$ is a finite 3-connected planar graph (that is, a polyhedral graph), then there is a pair of primal–dual circle packings: one packing whose intersection graph is isomorphic to $G$, and another whose intersection graph is isomorphic to the planar dual of $G$, such that for every vertex in $G$ and face adjacent to it, the circle in the first packing corresponding to the vertex intersects orthogonally with the circle in the second packing corresponding to the face. For instance, applying this result to the graph of the tetrahedron gives, for any four mutually tangent circles, a second set of four mutually tangent circles each of which is orthogonal to three of the first four. The circle packing for a maximal planar graph is automatically part of a pair of primal–dual circle packings, because each triple of tangent circles in the primal packing has a dual circle that passes at right angles through its three points of tangency. Like the circle packing for a maximal planar graphs, primal–dual circle packings are unique up to reflections and Möbius transformations. A further generalization, replacing intersection angle with inversive distance, allows the specification of packings in which some circles are required to be disjoint from each other rather than crossing or being tangent.

Yet another variety of generalizations allow shapes that are not circles. Suppose that each vertex $v$ of a finite planar graph $G$ corresponds to a smooth convex set $K_{v}\subset \mathbb {R} ^{2}$. Then there is a packing $P=(K'_{v}:v\in V)$ in the plane whose tangencies correspond one-for-one with the edges of $G$ where each set $K'_{v}$ is obtained from $K_{v}$ by translating and scaling. This result, from Oded Schramm's 1990 Ph.D. thesis, is a special case of Schramm's "monster packing theorem". The "monster" of the theorem is a spanning tree of the given graph, with a function for each vertex specifying how the shape it should be packed with depends on the relative positions of tangencies around all the shapes, satisfying certain consistency conditions. To prove that monsters can always be packed, Schramm followed Thurston's proof of the circle packing theorem, using the Brouwer fixed point theorem. He wrote that "One can just see the terrible monster swinging its arms in sheer rage, the tentacles causing a frightful hiss, as they rub against each other."

Other properties

Relative radii

Construction for rings of circles achieving the most extreme ratio of inner radius to surrounding radius in the ring lemma

Main article: Ring lemma

A result known as the ring lemma controls the sizes of adjacent circles in a Euclidean circle packing. According to the ring lemma, if one circle in a packing is surrounded by a ring of $d$ others, then the ratios of the inner circle's radius to the radius of each surrounding circle is at most exponential in $d$. More precisely, this ratio is at most $F_{2d-1}-1$, where $F_{i}$ denotes the $i$th Fibonacci number.

Monotonicity of angles

In the triangle connecting the centers of three mutually tangent circles, the angle formed at the center of one of the circles is monotone decreasing in its radius and monotone increasing in the two other radii. Beardon & Stephenson (1991) described related monotonicity properties of circle packings in the hyperbolic plane that they describe as being a discrete analogue to the Schwarz–Pick theorem in complex differential geometry. They consider any finite circle packing in the hyperbolic plane whose coin graph has the structure of a triangulated disk, and they compare this packing to another packing representing the same graph, obtained by treating the line at infinity of the hyperbolic plane as another circle, tangent to all the circles on the outer boundary of the disk (which become horocycles of infinite radius in the second packing). They prove that in the second packing, each circle's radius is non-decreasing, as is the hyperbolic distance between each pair of centers of tangent circles. If any of the radii or distances is equal, then they all are, and the two packings are congruent.

Ordering by radii

A Koebe ordering is the sequence of vertices of a planar graph, ordered by their radii in a circle packing (larger to smaller). If there are no ties (which can be achieved by performing a Möbius transformation) then in the resulting ordering each vertex has at most five earlier neighbors, matching the worst-case degeneracy of planar graphs. This property has been generalized as the $d$-admissability of the ordering, the maximum number of disjoint paths of at most $d$ steps that all start at the same vertex $v$, continue through vertices later than $v$ in the ordering, and end at a vertex earlier than $v$. Any Koebe ordering has $d$-admissability $O(d/\log d)$, best possible for planar graphs to within a constant factor.

Triangulated packings of surfaces

A periodic triangulated packing of the plane with three radii within 0.651 of each other, conjectured by Connelly & Zhang (2025) to have the closest ratio to 1 of any non-hexagonal packing

Instead of starting with a topological embedding of a graph, and searching for a surface with uniform geometry on which that graph can be represented by a circle packing, several authors have studied a reversed version of this question: which uniform surfaces admit triangulated packings, circle packings for which each gap between circles is a circular horn triangle surrounded by three tangent circles? By the uniqueness part of the circle packing theorem, each packing is uniquely determined (up to symmetries of the surface) by its graph of tangencies, but for this problem, the graph of tangencies is determined from the geometry, rather than vice versa.

Among periodic infinite triangulated packings of the Euclidean plane, there is only one triangulated packing with a single radius, the hexagonal packing. There are nine distinct pairs of radii (normalized so the maximum radius is one), and 164 triples of radii, that form triangulated packings. In general the number of $k$-tuples of radii that can form a triangulated packing is finite, but with an unknown growth rate as a function of $k$. The ratio of the smallest to largest radius is at most 0.701 for any triangulated packing other than the hexagonal packing, for which this ratio is 1. There is a packing with radius ratio approximately 0.651, with three distinct radii; it has been conjectured by Connelly & Zhang (2025) to have the largest possible radius ratio of any non-hexagonal triangulated packing.

A circular rectangle with Brooks invariant 3 + 1/(2 + 1/4) = 31/9

Brooks (1986) describes a method of continuously associating a real number as an invariant of a circular rectangle, the region $R$ bounded by a cycle of four tangent circles (which may be given the symmetries of a rectangle by a Möbius transformation), in such a way that when the invariant is a rational number, the rectangle has a triangulated packing. His method first packs a chain of circles tangent to the top and bottom sides of $R$, with the leftmost circle in the chain tangent to the left side of $R$; let $r_{1}$ be the number of circles that can be packed in this way without overlapping the right side of $R$. This chain leaves a smaller circular rectangle between its rightmost circle and the right side of the starting rectangle; pack this rectangle recursively in the same way with another chain of circles, tangent to its left and right sides, and let $r_{2}$ be the number of circles in this second chain. This packing process may continue forever, giving an infinite sequence of positive integers $r_{i}$, the numbers of circles in each chain, or it may terminate after a finite number of stages with a triangulated packing. Regardless, Brooks defines his invariant $r(R)$ to be the simple continued fraction $$r(R)=r_{1}+{\frac {1}{r_{2}+{\frac {1}{r_{3}+\cdots }}}}.$$ This is a rational number if and only if this packing process terminates with a finite triangulated packing.

Not every uniform surface admits a triangulated packing. For instance, in the case of flat tori (the quotient spaces of the Euclidean plane by a lattice, obtained by gluing opposite edges of a parallelogram), the geometry can vary continuously but, by the uniqueness of toroidal circle packings, only countably many distinct tori (up to scaling) have triangulated packings, and in particular they must have shapes that can be described by algebraic numbers. Nevertheless, Brooks (1986) showed that, for each possible genus of compact surfaces, the surfaces that have triangulated packings form a dense set in the Teichmuller space of all surfaces with that genus. This means that, for any given uniform compact surface, there exists another uniform compact surface, with almost the same geometry, on which there exists a triangulated packing. To prove this, Brooks first considers packings in which all gaps between triangles have either three or four sides, which can be obtained by placing circles to break up gaps with more sides into pieces with fewer sides. He then deforms each circular rectangle obtained in this way into a nearby rectangle whose invariant is rational to obtain a triangulated packing within each of the deformed rectangles. This produces a triangulation of the whole surface which, by the circle packing theorem, can be represented by a circle packing on a different uniform surface, slightly deformed from the given surface.

Applications

The circle packing theorem is a useful tool to problems including conformal maps, polyhedral realization of graphs, the planar separator theorem, graph drawing, random walks on planar graphs, and the visualization of the human brain.

Conformal mapping

Circle packings can be used to approximate conformal mappings between specified domains. Each circle on the left corresponds to a circle on the right.

A conformal map between two open sets in the plane or in a higher-dimensional space is a continuous function from one set to the other that preserves the angles between any two curves. The Riemann mapping theorem, formulated by Bernhard Riemann in 1851, states that, for any two open topological disks in the plane, there is a conformal map from one disk to the other. Conformal mappings have applications in mesh generation, map projection, and other areas. However, it is not always easy to construct a conformal mapping between two given domains in an explicit way.

A construction of William Thurston uses circle packings to approximate conformal mappings. More precisely, this construction maps an arbitrary open disk $A$ to the interior $C$ of a circle; the mapping from one topological disk $A$ to another disk $B$ could then be found by composing the map from $A$ to $C$ with the inverse of the map from $B$ to $C$. Thurston's idea was to pack circles of some small radius $r$ in a hexagonal tessellation of the plane, within region $A$, leaving a narrow region near the boundary of $A$, of width $r$, where no more circles of this radius can fit. He then constructs a maximal planar graph $G$ from the intersection graph of the circles, together with one additional vertex adjacent to all the circles on the boundary of the packing. By the circle packing theorem, this planar graph can be represented by a circle packing within circle $C$ in which all the edges (including the ones incident to the boundary vertex) are represented by tangencies of circles. The circles from the packing of $A$ correspond one-for-one with the circles within $C$, with the circle that forms the boundary of $C$ corresponding to the boundary of $A$.

This correspondence of circles can be used to construct a continuous function from $A$ to the interior of $C$ in which each circle and each gap between three circles is mapped from one packing to the other by a Möbius transformation. As $n$ goes to infinity, the function $f_{n}$ determined using Thurston's method from hexagonal packings of radius-$1/n$ circles converges uniformly on compact subsets of $A$ to a conformal map from $A$ to $C$. More generally, this holds for sequences of packings that are not necessarily hexagonal packings, as long as the sequence of maximum radii of the packings converges to zero. An alternative method hexagonally packs circles of small radius into $C$, and constructs a combinatorially equivalent packing of circles into $A$, tangent to its boundary; it converges in the same way. Practical applications of this method have been hindered by the difficulty of computing circle packings and by its relatively slow convergence rate. However, it has some advantages when applied to non-simply-connected domains and in selecting initial approximations for numerical techniques that compute Schwarz–Christoffel mappings, a different technique for conformal mapping of polygonal domains.

This construction of approximate conformal maps can also be described in terms of supplying a uniform geometry to a topological surface, and it can be extended from the surface itself to other objects embedded within the surface. An example comes from dessins d'enfant, a certain type of graph embedding used in algebraic geometry to study Riemann surfaces and the absolute Galois group. These automatically come with a triangulation, within which the dessin is a subset of the edges, but these triangulations may form multigraphs rather than simple graphs. By applying the circle packing theorem to subdivisions of these triangulations, an approximation of the dessin on a surface of uniform geometry may be constructed.

Quasiconformal mapping

When a conformal mapping is not possible, it may still may be possible to obtain a quasiconformal mapping. Conformal mappings are smooth mappings from one Riemannian surface to another that, in the limit of small neighborhoods around any point, map circles to circles. Instead, quasiconformal mappings may, in the same limit, map circles to ellipses of bounded eccentricity, with smaller deformation as the bound on eccentricity approaches one. As one application of this idea, Hurdal & Stephenson (2004) apply circle packing to the problem of constructing a flattened map of the functional regions of the human brain. To do this, they triangulate a three-dimensional model of the brain surface, find a circle packing representing the triangulation, and construct a piecewise-linear mapping from the triangles of the triangulated brain to the triangles of circle centers in the packing. They argue that this produces a quasiconformal mapping and therefore that it preserves the approximate shape of brain structures.

Brooks (1986) uses this idea in a different way, to study Kleinian groups, discrete subgroups of the symmetries of three-dimensional hyperbolic space. A Kleinian group is geometrically finite if it has a fundamental domain that is the intersection of finitely many half-spaces. Brooks shows that any geometrically finite group can be transformed by a quasiconformal mapping of arbitrarily small distortion into a subgroup of a Kleinian group with a fundamental domain of finite volume. If, moreover, the given Kleinian group has no cusps (either points at infinity where two bounding planes of the fundamental domain meet tangentially, or isolated points at infinity) it can be transformed by a quasiconformal mapping of arbitrarily small distortion into a subgroup of a Kleinian group with a compact fundamental domain, without points at infinity. The proof involves finding triangulated packings of surfaces whose geometry approximates the Riemann surfaces at the ends of the fundamental domain (the connected components of its points at infinity). The circles of these packings generate another Kleinian group, within which the circles coming from the boundaries of the fundamental domain generate a subgroup, close to the originally given group. Williams (2019) uses similar ideas to construct quasiconformal maps from a specified domain to the unit disk, having a specified distortion function.

Random walks

Several applications of the circle packing theorem use it to study random walks on planar graphs, based on the intuition that the approximation to conformal mapping of a circle packing can be used to relate these walks to Brownian motion, a geometric random process that is invariant under conformal maps. One result in this direction is that unbiased limit graphs of bounded-degree planar rooted graphs are almost surely recurrent, meaning that random walks on these graph limits almost surely return to the root infinitely often. The proof involves finding a circle packing that represents the limit graph, and using the ring lemma to bound the sizes of circles a small number of steps from the start of the walk, allowing the walk to be compared to a random walk on an integer grid. Jonnason & Schramm (2000) used circle packings to prove that the expected cover time of a random walk on every $n$-vertex planar graph (the average number of steps of the walk before all vertices are visited) is $\Omega (n\log ^{2}n)$.

Instead of using methods from Brownian motion to understand random walks on graphs, circle packings can also be used to find graphs whose random walks approximate Brownian motion. For the same sequences of refined circle packings used to approximate conformal mappings of a domain, a random walk on the associated coin graph will reach a boundary vertex with a probability that approaches, in the limit as the circle packings become more fine, the probability that a Brownian motion will reach a nearby point on the boundary of the domain.

Polyhedral realization and planar separators

A polyhedron and its midsphere. The red circles on the sphere (its horizons as viewed from the polyhedron vertices), and the blue domes where the midsphere protrudes through the polyhedron, form orthogonal spherical circle packings of the graph of the polyhedron and its dual graph.

Main article: Midsphere

The primal–dual packing of any polyhedral graph can be lifted from the plane to a sphere by stereographic projection. It can then be used to construct a convex polyhedron that has the given graph as its vertices and edges and that has a midsphere, a sphere tangent to all of the edges of the polyhedron. Each vertex of the polyhedron lies outside the sphere, at the apex of a cone that is tangent to the sphere along the circle corresponding to that vertex. This circle forms the horizon on the sphere, as viewed from the vertex. Each face of the polyhedron lies on the plane through its corresponding circle. Each edge of the polyhedron passes from one cone apex to another through the point of tangency of two circles, where both cones are tangent to the sphere. Conversely, if a polyhedron has a midsphere, then the circles formed by the intersections of the sphere with the polyhedron faces and the circles formed by the horizons on the sphere as viewed from each polyhedron vertex form a dual packing of this type.

Möbius transformations of the sphere lead to geometrically different polyhedron realizations. One particular realization, called the canonical polyhedron, is obtained by using a unit sphere and choosing a Möbius transformation that causes the center of the sphere to coincide with the centroid of the points of tangency of the polyhedron edges. All combinatorially equivalent polyhedra will produce in this way the same canonical polyhedron, up to rotations of the sphere. An alternative proof of the planar separator theorem, originally proved in a different way by Lipton and Tarjan, uses a similar idea of applying a Möbius transformation to a spherical circle packing. The construction obtains a circle packing on a sphere, representing the given graph. Next, a Möbius transformation of the sphere is used to transform a centerpoint of the circle centers, a point in space such that every plane through the centerpoint divides the $n$ centers into two subsets that each have size $\leq 3n/4$, to coincide with the center of the sphere. A uniformly random plane through the center of the sphere intersects $O({\sqrt {n}})$ of the circles of any packing of $n$ circles, in expectation. For the circle packing with the centerpoint at the sphere center, the vertices corresponding to these intersected circles form a separator that, when removed from the graph, leaves connected subgraphs of at most $3n/4$ vertices. Circle packing has also been used to explain the success of spectral methods for constructing separators for graphs of bounded genus and bounded degree.

Graph drawing

Circle packing has been used as a frequent tool in graph drawing, the study of methods for visualizing graphs. Fáry's theorem, that every graph that can be drawn without crossings in the plane using curved edges can also be drawn without crossings using straight line segment edges, follows as a simple corollary of the circle packing theorem: by placing vertices at the centers of the circles and drawing straight edges between them, a straight-line planar embedding is obtained.

Malitz & Papakostas (1994) apply circle packing to angular resolution, a measure of the quality of a graph drawing defined by the sharpest angle any two edges form at a shared vertex. They show that planar graphs of bounded maximum degree have drawings of bounded angular resolution, using circle packing. To do this, they derive a version of the ring lemma and use it to prove that the angular resolution of the drawing in which each vertex is placed at the center of its circle is at least an inverse-exponential function of the degree. Keszegh, Pach & Pálvölgyi (2013) use a more complicated strategy for placing vertices, near the circle centers on subdivisions of integer lattices, in order to find drawings where the number of distinct edge slopes (the slope number) is at most an exponential function of the degree.

Primal–dual circle packings in the plane can be used to obtain simultaneous orthogonal drawings, straight-line planar drawings of any polyhedral graph and its dual graph, with one dual vertex at infinity, so that each primal and dual pair of edges cross at right angles. Such a drawing can be obtained from a primal–dual circle packing for which one dual circle surrounds the others, with all vertices (except the outer dual vertex) placed at the center of the corresponding circle. The use of circle packings to construct these drawings resolves a problem posed by W. T. Tutte in 1963. A pointed drawing of a given planar graph, in which the edges are drawn as smooth curves that, at each vertex, leave it in the same direction as each other, may be obtained by placing each vertex on the circle of a circle packing (rather than at its center) and drawing each edge as a biarc formed by two circular arcs, perpendicular to the circles of the packing, through the point of tangency of two circles. Circle packings have also been used to obtain strongly monotone drawings of polyhedral graphs. These are straight-line drawings in which each two vertices are connected by a polygonal path that is monotone with respect to the line segment between the two vertices (its orthogonal projection onto this line segment is one-to-one). Another construction involving circle packing produces a Lombardi drawing for any subcubic planar graph, a drawing resembling a two-dimensional soap bubble foam in which the edges are drawn as circular arcs that meet at equal angles at each vertex.

Algorithmic aspects

When a circle packing exists, it exists with algebraic numbers for its center and radii, solving a system of quadratic equations that represent the requirements that each two centers of tangent circles be at a distance from each other equal to the sum of their radii. Therefore, in principle, it is possible to find circle packings using methods from symbolic computation for solving systems of polynomial equations, such as the Gröbner basis method. However, this approach can require the solution of high-degree polynomial equations, with unsolvable Galois groups. Instead, researchers have focused on more efficient numerical methods for finding accurate approximations to the centers and radii of circle packings.

One of the earliest and most versatile of these approximation results, announced by Bojan Mohar in 1993 with details in two subsequent papers, can be used to find primal–dual circle packings on surfaces of arbitrary genus, in time polynomial in the number of circles and in the number of bits of precision used to specify the output to the desired accuracy. Mohar's algorithm is an iterative method applied to the system of radii of a primal–dual circle packing, starting from an initial inaccurate system of radii. It considers the orthodiagonal quadrilaterals formed by each pair of crossing primal and dual edges. From a system of radii, one can calculate the angles of these quadrilaterals (if the circles could be packed with these radii): for a system of radii to form a packing, these angles should sum to $2\pi$ around each vertex. For systems of radii that do not give the correct sums, Mohar partitions the radii into a subset of radii that are too large (the angles around that vertex sum to less than $2\pi$ and a complementary subset of radii that are too small, and uses the bisection method to find two parameters $\beta$ and $\gamma$ such that multiplying the large radii by $\beta$ and the small radii by $\gamma$ reduces the mean squared error between the angle sums and $2\pi$. After sufficiently many repetitions of this process lead to an accurate system of radii, Mohar uses these radii to place the circle centers, starting from one primal–dual quadrilateral and then using the already-placed centers of each quadrilateral and the radii of its circles to determine the locations of the remaining centers. Although Mohar states that the algorithm runs in polynomial time, he does not state its polynomial time bound explicitly. Dong, Lee & Quanrud (2020) suggest that the computational complexity of Mohar's packing algorithm is at least quintic in the number of circles to be packed.

Collins & Stephenson (2003) provide a simpler iterative method that modifies only one circle radius at a time, again computing the system of circle radii before using the radii to place the circle centers. The version of the circle packing problem that they solve produces a circle packing in the Euclidean plane for a maximal planar graph, with a specified outer triangle and with specified radii for the three circles of this triangle. They begin with a set of tentative radii that do not correspond to a valid packing, and then repeatedly perform the following steps:

1. Choose an internal vertex $v$ of the input graph.
2. Calculate the total angle $\theta$ that its $k$ neighboring circles would cover around the circle for $v$, if the neighbors were placed tangent to each other and to the central circle using their tentative radii.
3. Determine a representative radius $r$ for the neighboring circles, such that $k$ circles of radius $r$ would give the same covering angle $\theta$ as the neighbors of $v$ give.
4. Set the new radius for $v$ to be the value for which $k$ circles of radius $r$ would give a covering angle of exactly $2\pi$.

Each of these steps may be performed with simple trigonometric calculations. Collins and Stephenson prove that, applied only to a single vertex, this method rapidly converges to a radius that gives covering angle $2\pi$. Further, they argue that the system also globally converges to a consistent system of radii, and they provide computational experiments suggesting that the rapid local convergence of this method extends to rapid global convergence of the entire system of radii. Once the system has converged, the circles may be placed one at a time, similarly to the algorithm of Mohar, at each step using the positions and radii of two neighboring circles to determine the center of each successive circle.

Another algorithm by Orick, Stephenson & Collins (2017) applies to the same planar packings as Collins & Stephenson (2003), and approximates both the system of radii and circle centers simultaneously and iteratively. It alternates between steps that use a weighted Tutte embedding to place the centers, and that use the resulting circle centers to determine improved radii. Although they provide no theoretical guarantees on the performance of this algorithm, Orick et al. claim that their experiments show linear convergence to a consistent packing in practice, which when true would lead to a polynomial time bound.

Dong, Lee & Quanrud (2020) again address the case of finding planar packings for maximal planar graphs, but with an explicit time bound. Although focused only on a primal circle packing, they work with the system of radii of a primal–dual packing, for maximal planar graphs only, with a dual circle for each triangular face of the graph. Like Mohar, they use orthodiagonal quadrilaterals determined by crossing pairs of primal and dual edges, with angles calculated from a given system of radii, which for a valid system of radii should sum to $2\pi$ at each vertex. Following Colin de Verdière (1991), they set up a convex optimization problem in which the variables to be optimized are the logarithms of the radii of the primal–dual packing, and the convex function to be minimized combines terms that are linear in these variables and in the antiderivatives of the arctangents of ratios of radii. They show that the minimizer of this function provides a system of radii that meet the conditions of a circle packing in that the angles of the quadrilaterals around each vertex sum to $2\pi$. By finding a spanning tree of the graph of orthogonal circles in the packing with the property that each spanning tree edge connects circles whose radii are not too far from each other, they prove that this function is strongly convex near its minimum, allowing the application of powerful methods from convex programming. Based on these techniques, they give a time bound for finding a packing of $${\tilde {O}}\left(n\log {\frac {R}{\varepsilon }}\right),$$ where the ${\tilde {O}}$ is a form of big O notation that suppresses terms that are logarithmic in its argument, $n$ is the number of circles to be packed, $R$ is the ratio between the largest and smallest radius in the resulting packing (which may be at worst exponential in $n$), and $\varepsilon$ is a parameter that controls how accurate the numerical approximation to the packing should be. All computed radii are within a $1+\varepsilon$ factor of the radius of an exact circle packing, and all computed centers are at a distance from the centers of an exact circle packing that is at most $\varepsilon$ times the radius of the smallest circle.

Yu et al. (2011) develop a numerical distributed algorithm based on a discrete version of Ricci flow to construct approximate primal–dual circle packings on a sphere. Their motivation is to use the midsphere polyhedra constructed from these packings for load-balanced position-based routing, following a scheme of Papadimitriou & Ratajczak (2005). According to this scheme, on a polyhedron with a midsphere, messages can be forwarded from vertex to a neighboring vertex of this polyhedron in a way that always increases the inner product of the three-dimensional coordinates of the current location and destination. The existence of a midsphere is used to prove that each message eventually reaches its destination.

History

An Apollonian gasket, mentioned by Leibniz in 1706

1911 image of a Doyle spiral from an article on plant growth

Ken Stephenson writes that "there is indeed a long tradition behind our story", and attributes the familiar hexagonal packing of congruent circles to folklore. Other early works on circle packings with specific patterns of tangency include:

• Descartes' theorem on the radii of four mutually tangent circles, stated by René Descartes in 1643 and by Japanese mathematician Yamaji Nushizumi in 1751,
• a 1706 letter by Leibniz mentioning a variant of the Apollonian gasket, an infinite fractal circle packing formed by repeatedly placing a circle within each circular triangle between larger circles in the packing, and
• the 1910 work of Arnold Emch on Doyle spirals in phyllotaxis (the mathematics of plant growth).

The circle packing theorem itself was first stated and proved by Paul Koebe in 1936. In the 1970s, William Thurston rediscovered the circle packing theorem, and noted that it followed from the work of E. M. Andreev. He mentioned these results in a 1978 talk at the International Congress of Mathematicians; in the same year, German mathematician Gerd Wegner also conjectured that the circle packing theorem holds. At the Bieberbach conference in 1985, Thurston proposed a scheme for using the circle packing theorem to obtain a homeomorphism of a simply connected proper subset of the plane onto the interior of the unit disk, and he conjectured that this scheme converges to the Riemann mapping as the radii of the circles tend to zero. Thurston's conjecture was proven in 1987 by Burton Rodin and Dennis Sullivan. Thurston's work in this area brought the topic of circle packings to the attention of mathematicians and led to the formation of a research community centered on this idea.

See also

• Ford circles, a packing of circles along the rational number line
• Steiner chain, a circle packing for the graph of a bipyramid

References

• Aharonov, Dov (1997), "The sharp constant in the ring lemma", Complex Variables, 33 (1–4): 27–31, doi:10.1080/17476939708815009, MR 1624890
• Aichholzer, Oswin; Rote, Günter; Schulz, André; Vogtenhuber, Birgit (2012), "Pointed drawings of planar graphs", Computational Geometry, 45 (9): 482–494, doi:10.1016/j.comgeo.2010.08.001, MR 2926292
• Alam, Md. Jawaherul; Eppstein, David; Goodrich, Michael T.; Kobourov, Stephen G.; Pupyrev, Sergey (2014), "Balanced circle packings for planar graphs", in Duncan, Christian A.; Symvonis, Antonios (eds.), Graph Drawing - 22nd International Symposium, GD 2014, Würzburg, Germany, September 24-26, 2014, Revised Selected Papers, Lecture Notes in Computer Science, vol. 8871, Springer, pp. 125–136, arXiv:1408.4902, doi:10.1007/978-3-662-45803-7_11
• Andreev, E. M. (1970a), "Convex polyhedra in Lobačevskiĭ spaces", Matematicheskii Sbornik, New Series, 81 (123): 445–478, doi:10.1070/SM1970v010n03ABEH001677, MR 0259734
• Andreev, E. M. (1970b), "Convex polyhedra of finite volume in Lobačevskiĭ space", Matematicheskii Sbornik, New Series, 83 (125): 256–260, doi:10.1070/SM1970v012n02ABEH000920, MR 0273510
• Bannister, Michael J.; Devanny, William E.; Eppstein, David; Goodrich, Michael T. (2015), "The Galois complexity of graph drawing: why numerical solutions are ubiquitous for force-directed, spectral, and circle packing drawings", Journal of Graph Algorithms and Applications, 19 (2): 619–656, doi:10.7155/jgaa.00349, MR 3430492
• Beardon, Alan F.; Stephenson, Kenneth (1990), "The uniformization theorem for circle packings", Indiana Univ. Math. J., 39 (4): 1383–1425, doi:10.1512/iumj.1990.39.39062
• Beardon, Alan F.; Stephenson, Kenneth (1991), "The Schwarz–Pick lemma for circle packings", Illinois J. Math., 35 (4): 577–606, doi:10.1215/ijm/1255987673
• Benjamini, Itai; Schramm, Oded (2001), "Recurrence of distributional limits of finite planar graphs", Electronic Journal of Probability, 6, doi:10.1214/EJP.v6-96, MR 1873300
• Bos, Erik-Jan (2010), "Princess Elizabeth of Bohemia and Descartes' letters (1650–1665)", Historia Mathematica, 37 (3): 485–502, doi:10.1016/j.hm.2009.11.004
• Bowers, Philip L.; Stephenson, Kenneth (2004), Uniformizing Dessins and Belyĭ Maps via Circle Packing, Memoirs of the American Mathematical Society, vol. 170, doi:10.1090/memo/0805, MR 2053391
• Brightwell, Graham R.; Scheinerman, Edward R. (1993), "Representations of planar graphs", SIAM Journal on Discrete Mathematics, 6 (2): 214–229, doi:10.1137/0406017
• Brooks, Robert (1986), "Circle packings and co-compact extensions of Kleinian groups", Inventiones Mathematicae, 86 (3): 461–469, doi:10.1007/BF01389263, MR 0860677
• Carter, Ithiel; Rodin, Burt (1992), "An inverse problem for circle packing and conformal mapping", Transactions of the American Mathematical Society, 334 (2): 861–875, doi:10.1090/S0002-9947-1992-1081937-X
• Chow, Bennett; Luo, Feng (2003), "Combinatorial Ricci flows on surfaces", Journal of Differential Geometry, 63 (1): 97–129, MR 2015261
• Colin de Verdière, Yves (1991), "Une principe variationnel pour les empilements de cercles", Inventiones Mathematicae, 104 (1): 655–669, doi:10.1007/BF01245096
• Collins, Charles R.; Stephenson, Kenneth (2003), "A circle packing algorithm", Computational Geometry. Theory and Applications, 25 (3): 233–256, doi:10.1016/S0925-7721(02)00099-8, MR 1975216
• Connelly, Robert; Gortler, Steven J. (2021), "Packing disks by flipping and flowing" (PDF), Discrete & Computational Geometry, 66 (4): 1262–1285, arXiv:1910.02327, doi:10.1007/s00454-020-00242-8, MR 4333292
• Connelly, Robert; Zhang, Zhen (2025), "Rigidity of circle packings with flexible radii", Discrete & Computational Geometry, 74 (3): 585–618, arXiv:2206.07165, doi:10.1007/s00454-025-00776-9, MR 4965850
• Coxeter, H. S. M. (2006), "An absolute property of four mutually tangent circles", Non-Euclidean geometries, Math. Appl. (N. Y.), vol. 581, New York: Springer, pp. 109–114, doi:10.1007/0-387-29555-0_5, ISBN 978-0-387-29554-1, MR 2191243
• de Fraysseix, Hubert; Ossona de Mendez, Patrice; Rosenstiehl, Pierre (1994), "On triangle contact graphs", Combinatorics, Probability and Computing, 3 (2): 233–246, doi:10.1017/S0963548300001139, MR 1288442
• Dong, Sally; Lee, Yin Tat; Quanrud, Kent (2020), "Computing circle packing representations of planar graphs", in Chawla, Shuchi (ed.), Proceedings of the 2020 ACM-SIAM Symposium on Discrete Algorithms, SODA 2020, Salt Lake City, UT, USA, January 5–8, 2020, Society for Industrial and Applied Mathematics, pp. 2860–2875, arXiv:1911.00612, doi:10.1137/1.9781611975994.174
• Dubejko, Tomasz (1997), "Circle-packing connections with random walks and a finite volume method", Séminaire de Théorie Spectrale et Géométrie, No. 15, Année 1996–1997, vol. 15, Univ. Grenoble I, Saint-Martin-d'Hères, pp. 153–161, doi:10.5802/tsg.187, MR 1604271
• Emch, Arnold (1910), "Sur quelques exemples mathématiques dans les sciences naturelles", L'Enseignement mathématique (in French), 12: 114–123
• Eppstein, David (2014), "A Möbius-invariant power diagram and its applications to soap bubbles and planar Lombardi drawing", Discrete & Computational Geometry, 52 (3): 515–550, doi:10.1007/s00454-014-9627-0, MR 3257673
• Felsner, Stefan; Igamberdiev, Alexander; Kindermann, Philipp; Klemz, Boris; Mchedlidze, Tamara; Scheucher, Manfred (2016), "Strongly monotone drawings of planar graphs", in Fekete, Sándor P.; Lubiw, Anna (eds.), 32nd International Symposium on Computational Geometry, SoCG 2016, Boston, MA, USA, June 14–18, 2016, LIPIcs, vol. 51, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, pp. 37:1–37:15, doi:10.4230/LIPICS.SOCG.2016.37
• Felsner, Stefan; Rote, Günter (2019), "On primal–dual circle representations", in Fineman, Jeremy T.; Mitzenmacher, Michael (eds.), 2nd Symposium on Simplicity in Algorithms, SOSA 2019, San Diego, CA, USA, January 8–9, 2019, OASIcs, vol. 69, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, pp. 8:1–8:18, doi:10.4230/OASICS.SOSA.2019.8
• Fernique, Thomas (2025), "Packing unequal disks in the Euclidean plane", Computational Geometry, 124/125 102134, arXiv:2305.12919, doi:10.1016/j.comgeo.2024.102134, MR 4784743
• Hansen, Lowell J. (1988), "On the Rodin and Sullivan ring lemma", Complex Variables, 10 (1): 23–30, doi:10.1080/17476938808814284, MR 0946096
• He, Zheng-Xu; Schramm, Oded (1993), "Fixed points, Koebe uniformization and circle packings", Annals of Mathematics, Second Series, 137 (2): 369–406, doi:10.2307/2946541, JSTOR 2946541, MR 1207210
• He, Zheng-Xu; Schramm, O. (1995), "Hyperbolic and parabolic packings", Discrete & Computational Geometry, 14 (2): 123–149, doi:10.1007/BF02570699, MR 1331923
• He, Zheng-Xu; Schramm, Oded (1996), "On the convergence of circle packings to the Riemann map", Inventiones Mathematicae, 125 (2): 285–305, doi:10.1007/s002220050076, MR 1395721
• Hurdal, Monica K.; Stephenson, Ken (January 2004), "Cortical cartography using the discrete conformal approach of circle packings", NeuroImage, 23: S119 – S128, doi:10.1016/j.neuroimage.2004.07.018
• Jonnason, Johan; Schramm, Oded (2000), "On the cover time of planar graphs", Electronic Communications in Probability, 5: 85–90, doi:10.1214/ECP.v5-1022
• Kapovich, Michael (2001), "Chapter 13: Brooks' theorem and circle packings", Hyperbolic manifolds and discrete groups, Progress in Mathematics, vol. 183, Boston, Massachusetts: Birkhäuser Boston, pp. 333–350, doi:10.1007/978-0-8176-4913-5_13, ISBN 0-8176-3904-7, MR 1792613
• Kelner, Jonathan A. (2006), "Spectral partitioning, eigenvalue bounds, and circle packings for graphs of bounded genus", SIAM Journal on Computing, 35 (4): 882–902, doi:10.1137/S0097539705447244, MR 2203731; also published as a 2005 MIT master's thesis, hdl:1721.1/30169
• Keszegh, Balázs; Pach, János; Pálvölgyi, Dömötör (2013), "Drawing planar graphs of bounded degree with few slopes", SIAM Journal on Discrete Mathematics, 27 (2): 1171–1183, doi:10.1137/100815001, MR 3071400
• Koebe, Paul (1936), "Kontaktprobleme der konformen Abbildung", Ber. Sächs. Akad. Wiss. Leipzig, Math.-Phys. Kl., 88: 141–164
• Leibniz, Gottfried Wilhelm (March 11–17, 1706), Letter to des Bosses, translated by Ottaviani, Osvaldo – via Technion
• Lipton, Richard J.; Tarjan, Robert E. (1979), "A separator theorem for planar graphs", SIAM Journal on Applied Mathematics, 36 (2): 177–189, CiteSeerX 10.1.1.104.6528, doi:10.1137/0136016
• Louder, Larsen; Mishchenko, Andrey M.; Souto, Juan (2014), "Three techniques for obtaining algebraic circle packings", Michigan Mathematical Journal, 63 (3): 535–552, arXiv:1304.1488, doi:10.1307/mmj/1409932632, MR 3255690
• Malitz, Seth; Papakostas, Achilleas (1994), "On the angular resolution of planar graphs", SIAM Journal on Discrete Mathematics, 7 (2): 172–183, doi:10.1137/S0895480193242931, MR 1271989
• Michiwaki, Yoshimasa (2008), "Geometry in Japanese mathematics", in Selin, Helaine (ed.), Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Springer Netherlands, pp. 1018–1019, doi:10.1007/978-1-4020-4425-0_9133, ISBN 978-1-4020-4559-2
• Miller, Gary L.; Teng, Shang-Hua; Thurston, William; Vavasis, Stephen A. (1997), "Separators for sphere-packings and nearest neighbor graphs", Journal of the ACM, 44 (1): 1–29, doi:10.1145/256292.256294
• Mohar, Bojan (1993), "A polynomial time circle packing algorithm", Discrete Mathematics, 117 (1–3): 257–263, doi:10.1016/0012-365X(93)90340-Y
• Mohar, Bojan (1997a), "Circle packings of maps in polynomial time", European Journal of Combinatorics, 18 (7): 785–805, doi:10.1006/eujc.1996.0135, MR 1478825
• Mohar, Bojan (1997b), "Circle packings of maps—the Euclidean case", Rendiconti del Seminario Matematico e Fisico di Milano, 67: 191–206, doi:10.1007/BF02930499, MR 1781041
• Nachmias, Asaf (2020), "Chapter 3: The Circle Packing Theorem", Planar Maps, Random Walks and Circle Packing: École d’Été de Probabilités de Saint-Flour XLVIII - 2018, Lecture Notes in Mathematics, Springer International Publishing, pp. 33–46, doi:10.1007/978-3-030-27968-4_3, ISBN 9783030279684
• Nederlof, Jesper; Pilipczuk, Michał; Węgrzycki, Karol (2023), "Bounding generalized coloring numbers of planar graphs using coin models", Electronic Journal of Combinatorics, 30 (3) 3.33, arXiv:2201.09340, doi:10.37236/11095, MR 4644253
• Orick, Gerald L.; Stephenson, Kenneth; Collins, Charles (2017), "A linearized circle packing algorithm", Computational Geometry, 64: 13–29, doi:10.1016/j.comgeo.2017.03.002, MR 3638944
• Papadimitriou, Christos H.; Ratajczak, David (2005), "On a conjecture related to geometric routing", Theoretical Computer Science, 344 (1): 3–14, doi:10.1016/j.tcs.2005.06.022, MR 2178923
• Pisanski, Tomaž; Randić, Milan (2000), "Bridges between geometry and graph theory" (PDF), in Gorini, Catherine A. (ed.), Geometry at Work, MAA Notes, vol. 53, Cambridge University Press, pp. 174–194, MR 1782654, archived from the original (PDF) on 2022-01-19, retrieved 2017-02-19; see especially p. 176
• Rodin, Burton; Sullivan, Dennis (1987), "The convergence of circle packings to the Riemann mapping", Journal of Differential Geometry, 26 (2): 349–360, doi:10.4310/jdg/1214441375
• Rohde, Steffen (2011), "Oded Schramm: from circle packing to SLE", Annals of Probability, 39 (5): 1621–1667, arXiv:1007.2007, doi:10.1214/10-AOP590; also printed in Selected Works of Oded Schramm, Springer, 2011, doi:10.1007/978-1-4419-9675-6_1
• Sachs, Horst (1994), "Coin graphs, polyhedra, and conformal mapping", Discrete Mathematics, 134 (1–3): 133–138, doi:10.1016/0012-365X(93)E0068-F, MR 1303402, Zbl 0808.05043
• Schramm, Oded (1990), Packing Two-Dimensional Bodies With Prescribed Combinatorics And Applications To The Construction of Conformal and Quasi-Conformal Mappings (Ph.D. thesis), Princeton University, ProQuest 303827410; modified and reprinted as "Combinatorically Prescribed Packings and Applications to Conformal and Quasiconformal Maps", arXiv:0709.0710, 2007
• Schramm, Oded (1991), "Rigidity of infinite (circle) packings", Journal of the American Mathematical Society, 4 (1): 127–149, doi:10.1090/S0894-0347-1991-1076089-9, JSTOR 2939257, MR 1076089
• Schramm, Oded (1992), "How to cage an egg", Inventiones Mathematicae, 107 (3): 543–560, doi:10.1007/BF01231901, MR 1150601, Zbl 0726.52003
• Stephenson, Kenneth (1999), "The approximation of conformal structures via circle packing" (PDF), Computational methods and function theory 1997 (Nicosia), Ser. Approx. Decompos., vol. 11, World Scientific, pp. 551–582, MR 1700374
• Stephenson, Ken (2003), "Circle packing: a mathematical tale" (PDF), Notices of the American Mathematical Society, 50: 1376–1388
• Stephenson, Ken (2005), Introduction to Circle Packing: The Theory of Discrete Analytic Functions, Cambridge: Cambridge University Press
• Thurston, William (1985), The finite Riemann mapping theorem, invited talk at the International Symposium at Purdue University on the occasion of the proof of the Bieberbach conjecture
• Thurston, William (March 2002), "§13.6, Andreev's theorem and generalizations, and §13.7, Constructing patterns of circles", The Geometry and Topology of 3-manifolds, MSRI Publications, pp. 330–346, Electronic version 1.1, retrieved 2025-12-09
• Tutte, W. T. (1963), "How to draw a graph", Proceedings of the London Mathematical Society, Third Series, 13: 743–767, doi:10.1112/plms/s3-13.1.743, MR 0158387
• Williams, G. Brock (2019), "Constructing quasiconformal maps using circle packings and Brooks's parametrization of quadrilaterals", Annales Academiæ Scientiarum Fennicæ, 44 (2): 877–888, doi:10.5186/aasfm.2019.4445, MR 3973545
• Yu, Xiaokang; Ban, Xiaomeng; Zeng, Wei; Sarkar, Rik; Gu, Xianfeng; Gao, Jie (2011), "Spherical representation and polyhedron routing for load balancing in wireless sensor networks", INFOCOM 2011, 30th IEEE International Conference on Computer Communications, Joint Conference of the IEEE Computer and Communications Societies, 10–15 April 2011, Shanghai, China (PDF), IEEE, pp. 621–625, doi:10.1109/INFCOM.2011.5935240
• Ziegler, Günter M. (1995), Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152, Springer-Verlag, pp. 117–118, arXiv:math/9909177, doi:10.1007/978-1-4613-8431-1, ISBN 0-387-94365-X, MR 1311028, Zbl 0823.52002

External links

• CirclePack (free software for constructing circle packings from graphs, by Kenneth Stephenson, Univ. of Tennessee)
• CirclePackings, open source software for constructing circle packings from graphs, by Benjamin and Brice Loustau