Автокорреляционная функция

График 100 случайных величин, суммированный с синусоидальным сигналом малой амплитуды. График автокорреляционной функции позволяет увидеть периодичность в ряде данных.

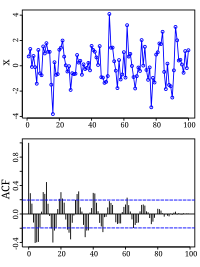
Автокорреляционная функция (АКФ) — зависимость взаимосвязи между функцией (сигналом) и её сдвинутой по аргументу функции копией от величины сдвига.

Для детерминированных сигналов автокорреляционная функция (АКФ) сигнала $f(t)$ определяется интегралом:

$B(\tau )=\int _{-\infty }^{\infty }f(t)f^{*}(t+\tau )dt=\int _{-\infty }^{\infty }f(t)f^{*}(t-\tau )dt,$

и показывает связь сигнала (функции $\;f(t)$) с копией самого себя, смещённого на величину $\tau$. Звёздочка означает комплексное сопряжение.

Для случайных процессов АКФ случайного процесса $X(t)$ имеет вид:

$B(t,t-\tau )=\mathbb {E} [X(t)X^{*}(t-\tau )]=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x_{1}x_{2}^{*}f_{2}(x_{1},t;x_{2},t-\tau )dx_{1}dx_{2}$,

где $\mathbb {E}$ — математическое ожидание,

$x_{1}$, $x_{2}^{*}$ — значения случайных величин $X(t)$ и $X^{*}(t-\tau )$ в моменты времени $t$ и $t-\tau$,

$f_{2}(x_{1},t;x_{2},t-\tau )$ — двумерная плотность вероятности случайных величин $X(t)$ и $X(t-\tau )$.

Также в литературе АКФ случайного процесса $X(t)$ определяют по формуле:

${\begin{aligned}B(t,t-\tau )=\mathbb {E} [(X(t)-\mathbb {E} [X(t)])(X^{*}(t-\tau )-\mathbb {E} [X^{*}(t-\tau )])]=\\=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }(x_{1}-\mathbb {E} [X(t)])(x_{2}^{*}-\mathbb {E} [X^{*}(t-\tau )])f_{2}(x_{1},t;x_{2},t-\tau )dx_{1}dx_{2}.\end{aligned}}$

В некоторых источниках эту функцию называют автоковариационной функций.

Если исходная функция строго периодическая, то на графике автокорреляционной функции тоже будет строго периодическая функция. Таким образом, из этого графика можно судить о периодичности исходной функции, а, следовательно, и о её частотных характеристиках. Автокорреляционная функция применяется для анализа сложных колебаний, например, электроэнцефалограммы человека.

Применение в технике

Корреляционные свойства кодовых последовательностей, используемых в широкополосных системах, зависят от типа кодовой последовательности, её длины, частоты следования её символов и от её посимвольной структуры.

Изучение автокорреляционной функции играет важную роль при выборе кодовых последовательностей с точки зрения наименьшей вероятности установления ложной синхронизации.

Другие применения

Автокорреляционная функция играет важную роль в математическом моделировании и анализе временных рядов, показывая характерные времена для исследуемых процессов. В частности, циклам в поведении динамических систем соответствуют максимумы автокорреляционной функции некоторого характерного параметра.

См. также

• Теорема Хинчина — Колмогорова
• Корреляционная функция
• Взаимнокорреляционная функция
• Периодическая функция
• Корреляция
• Критерий Дарбина — Уотсона
• Дисперсия случайной величины
• Свёртка (математический анализ)

Ссылки

• функция xcorr в MATLAB