Диэдральная симметрия в трёхмерном пространстве

Точечная группа в трёхмерном пространстве

Симметрии-инволюции Cs, (*) [ ] =	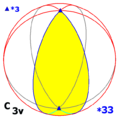Циклическая симметрия Cnv, (*nn) [n] =	Диэдральная симметрия Dnh, (*n22) [n,2] =
Группы многогранников, [n,3], (*n32)
Тетраэдральная симметрия Td, (*332) [3,3] =	Октаэдральная симметрия Oh, (*432) [4,3] =	Икосаэдральная симметрия Ih, (*532) [5,3] =

Диэдральная симметрия в трёхмерном пространстве — это одна из трёх бесконечных последовательностей точечных групп в трёхмерном пространстве, которые имеют группы симметрии, являющиеся абстрактными диэдральными группами Dih_n (для n ≥ 2).

Типы

Существует три типа диэдральной симметрии в трёхмерном пространстве, каждая показана ниже в трёх обозначениях: нотация Шёнфлиса, нотация Коксетера и орбифолдная нотация.

Хиральная

• D_n, [n,2]⁺, (22n) порядка 2n – диэдральная симметрия или пара-n-угольная группа

(абстрактная группа - Dih_n).

Ахиральные

• D_nh, [n,2], (*22n) порядка 4n – призматическая симметрия или полная орто-n-угольная группа

(абстрактная группа - Dih_n × Z₂).

• D_nd (или D_nv), [2n,2⁺], (2*n) порядка 4n – антипризматическая симметрия или полная гиро-n-угольная группа

(абстрактная группа - Dih_2n).

Для заданного n все три типа имеют вращательную симметрию порядка n вокруг одной оси (вращение на угол 360°/n не изменяет объект), и n вращательных симметрий порядка 2 для перпендикулярных осей. Для n = ∞ они соответствуют трём группам бордюра. Обозначения симметрий указаны в нотации Шёнфлиса, в квадратных скобках - в нотации Коксетера и в круглых скобках - в орбифолдной нотации. Термин «горизонтальный» (h) используется по отношению к вертикальной оси вращения.

В двумерном пространстве (на плоскости) группа симетрии D_n вклячает зеркальное отражение относительно прямых. Если плоскость вложена в трёхмерное пространство, такие отражения можно рассматривать либо как сужение на плоскость зеркального отражения относительно вертикальной плоскости, либо как сужение на плоскость вращения на 180° вокруг оси вращения. В трёхмерном пространстве две операции отличаются - группа D_n содержит только вращения и не содержит зеркальных отражений. Другая группа - циклическая или пирамидальная симметрия C_nv того же порядка 2n.

Вместе с зеркальной симметрией относительно плоскости, перпендикулярной оси вращения порядка n, мы имеем D_nh, [n], (*22n).

D_nd (или D_nv), [2n,2⁺], (2*n) имеет вертикальные плоскости отражения, проходящие между горизонтальными осями вращения, а не через них. Как результат, вертикальная ось является осью несобственного вращения порядка 2n.

D_nh является гуппой симметрии правильной n-угольной призмы, а также правильной n-угольной бипирамиды. D_nd является гуппой симметрии правильной n-угольной антипризмы, а также правильного n-угольного трапецоэдра. D_n является гуппой симметрии частично повёрнйтой призмы.

Случай n = 1 не включён, поскольку три типа симметрии равны следующим:

• D₁ и C₂ - группа порядка 2 простого вращения на 180°.
• D_1h и C_2v - группа порядка 4 с отражение относительно плоскости и поворотом на 180° вокруг прямой на этой плоскости.
• D_1d и C_2h - группа порядка 4 с отражением относительно плоскости и поворотом на 180° вокруг прямой, перпендикулярной плоскости.

Для n = 2 нет главной оси и двух дополнительных, а есть три равноправные оси.

• D₂, [2,2]⁺, (222) - группа порядка 4 является одним из трёх типов групп симметрии с четверной группой Кляйна в качестве абстрактной группы.

Симметрия имеет три перпендикулярные оси вращения второго порядка. Она является группой симметрии кубоида с буквой S, написанной на двух противоположных гранях с той же ориентацией.

• D_2h, [2,2], (*222) - группа порядка 8 является группой симметрии кубоида.
• D_2d, [4,2⁺], (2*2) - группа порядка 8 является группой симметрии, например, для многогранников
  • Квадратный кубодид с диагональю, нарисованной на одной из квадратных граней и перпендикулярной диагональю на другой грани.
  • Правильны тетраэдр, растянутый в направляени прямой, соединяющей середины двух противоположных рёбер (D_2d является подгруппой

T_d; путём растяжения мы уменьшаем симетрию).

Подгруппы

D2h, [2,2], (*222)

D4h, [4,2], (*224)

См. также: Циклическая симметрия в трёхмерном пространстве

Для D_nh, [n,2], (*22n) порядка 4n

• C_nh, [n⁺,2], (n*) порядка 2n
• C_nv, [n,1], (*nn) порядка 2n
• D_n, [n,2]⁺, (22n) порядка 2n

Для D_nd, [2n,2⁺], (2*n) порядка 4n

• S_2n, [2n⁺,2⁺], (n×) порядка 2n
• C_nv, [n⁺,2], (n*) порядка 2n
• D_n, [n,2]⁺, (22n) порядка 2n

D_nd является также подгруппой группы D_2nh.

Примеры

D2h, [2,2], (*222) порядок 8	D2d, [4,2+], (2*2) порядок 8	D3h, [3,2], (*223) порядок 12
Контуры швов баскетбольного мяча	Контуры швов бейсбольного мяча (игнорируем направленность шва)	Пляжный мяч (игнорируем раскраску)

D_nh, [2,n], (*22n):

призмы

D_5h, [2,5], (*225):

Пентаграмная призма

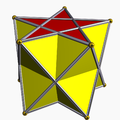Пентаграмная антипризма

D_4d, [8,2⁺], (2*4):

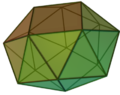Плосконосая квадратная антипризма

D_5d, [10,2⁺], (2*5):

Пятиугольная антипризма

Пентаграммная скрещенная антипризма

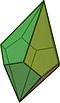Пятиугольный трапецоэдр

D_17d, [34,2⁺], (2*17):

Семиугольная антипризма

См. также

• Список групп сферической симметрии
• Точечная группа в трёхмерном пространстве
• Циклическая симметрия в трёхмерном пространстве

Литература

• H. S. M. Coxeter, W. O. J. Moser. Generators and Relations for Discrete Groups. — New York: Springer-Verlag, 1980. — ISBN 0-387-09212-9.
• N.W. Johnson. Chapter 11: Finite symmetry groups, 11.5 Spherical Coxeter groups // Geometries and Transformations. — 2018. — ISBN 978-1-107-10340-5.
• John Horton Conway, Daniel H. Huson. The Orbifold Notation for Two-Dimensional Groups // Structural Chemistry. — Springer Netherlands, 2002. — Т. 13, вып. 3. — С. 247–257. — doi:10.1023/A:1015851621002.

Ссылки

• Graphic overview of the 32 crystallographic point groups – form the first parts (apart from skipping n=5) of the 7 infinite series and 5 of the 7 separate 3D point groups