減法

| 算术运算 | ||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
減法(英语:substraction、法语:soustraction)是四则运算之一。减法运算的本质,就是「逆着加法去寻找原数」。
例如: 中,已知 是 和 的和,其中一个加数是 ,求另一个加数 。
其中, 稱為被減數, 稱為減數, 是 和 的差。
减法遵循几个重要的规律:
减法不像加法那样符合交換律,即改变运算顺序会一同改变结果符号。它也不满足结合律,也就是说,当需要连续减去两个以上的数时,减法的执行顺序会影响结果。由于 是加法單位元,减去 不会改变一个数的值。
此外,减法在涉及相关运算(如加法和乘法)时也遵循可预测的规则。所有这些规则皆可从整数减法开始进行证明,并推广至实数、乃至更广泛的数学对象。所有遵循这些规律的通用二元运算在抽象代数中都有研究。
定义
[编辑]
算术定义
[编辑]已知两个加数的和与其中一个加数,求另一个加数的运算,符号为“ ”,结果为差。
集合论定义
[编辑]在集合论中,减法通过差集定义。给定两个集合 和 ,它们的差集 包含所有属于 但不属于 的元素。例如:
若 ,,则 。
此外,在可计算性理论中,由于减法在自然数上并非良定义,数与数之间的运算实际上是通过“截断减法”或称为monus的运算来定义的。
代数结构中的定义
[编辑]例如,在整数环 中,减法确保对任意 ,存在唯一的 使得 。
符号与表示
[编辑]减法通常用被减数与减数之间的减号"-"来表示(中缀表示法的一种),运算结果则用等号“=”表示。例如:
- (2 减 1 等于 1)
- (4 减 6 等于 -2)
在某些情况下,即使没有出现减号,减法运算亦可“约定俗成”。例如在记账的一列数中,若下方数字以红色显示,则通常表示需要减去该列中较小的数,差值写在该行下方横线之下的位置。[1]
英语单词subtraction(减法,名词)来源于拉丁语动词“subtrahere”,而该动词本身由前缀“sub”(意为“(从)下方”)和动词“trahere”(意为“拉拽”)复合构成。[2]因此,减法的字面含义就是“从下方拉出”或“取走”。而subtrahend(减数)则由添加动名词后缀“-nd”派生(字面意义为“被拉出的事物”)。
minuend(被减数)则源于拉丁动词“minuere”(意为“减少或缩小”),表示“被缩减的事物”。[3]
性质
[编辑]恒等性质
[编辑]任何数减去 0 都等于其本身:。
非运算性质
[编辑]- 非交换律:
- 非结合律:
不同的减法运算
[编辑]自然数减法
[编辑]自然数集上的减法运算不满足封闭性:只有当被减数大于或等于减数时,差值才是自然数。例如 减去 就无法得到自然数结果。对此有两种处理方式:
整数减法
[编辑]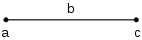
想象一条长度为 的线段,左端标记为 ,右端标记为 。从 点出发,向右移动 个单位即可到达 点。在数学上,这种右移通过加法运算建模:
而从 点出发,向左移动 个单位就能回到 点。这种左移则通过减法运算建模:

再想象一条线段,这条线段则标有数字 、 、 。现在从位置 出发,向左移动 个单位,仍停留在 ,因此 ;向左移动 个单位,则到达位置 ,因此 。
此线段的局限在于,无以描述从位置 向左移动 个单位后的情况,需延长数轴(即沿用整数数轴)方可。
分数减法
[编辑]分數减法类似自然数和整数的减法,但要求分母相同。若两分数分母不同,可用通分实现:
实数减法
[编辑]实数域可通过仅定义两个二元运算(加法与乘法)及两个一元运算(求加法逆元与乘法逆元)来构建。此时,从被减数中减去减数的实数运算,可定义为被减数与该减数加法逆元的加法运算。例如:
若不依赖这些一元运算,亦可将减法与除法作为基本二元运算来处理。
抽象代数减法
[编辑]向量减法
[编辑]在线性代数中,向量空间是一个允许向量相加及缩放的代数结构。所有实数的有序对组成的集合就是一个常见的向量空间:有序对 (a, b) 被解释为欧几里得平面上从原点到由 (a, b) 表示的点的向量。两个向量的差是通过将对应的坐标相减完成的:(a, b) - (c, d) = (a - c, b - d)。
矩阵减法
[编辑]大小相同的两个矩阵可以相减。两个 m × n 矩阵 A 和 B 的差也是一个 m × n 矩阵,用 A - B 表示,由对应元素相加得到:
基于群论的减法
[编辑]设 为一个阿贝尔群。我们在 中定义一个新的内合成法则,称为“减法”并记作"−",其定义为:
其中 表示元素 的逆元。
需要注意的是,既用"-"表示元素 的逆元 ,又表示二元运算 ,属于符号的滥用。
一般的减法运算性质在此群论框架下依然成立。
范畴论中的减法
[编辑]在范畴论中,减法并没有统一的直接对应物,但可以借助态射、核(kernel)、余核(cokernel)、差分对象等抽象概念来表达类似于“减法”的关系。
二进制减法
[编辑]在计算机科学和数字逻辑中,减法是在二进制数之间进行的,通常使用补码方法来简化运算,详见下文“计算机算法”。
运算方法
[编辑]竖式减法
[编辑]从右向左相减的方法
[编辑]美国竖式法
[编辑]在美国所谓的“传统教学”中,学生在一年级末(或二年级期间)会学习一种针对多位整数的特定竖式减法运算,该流程会在四年级或五年级时扩展至包含小数的分数表示形式。目前几乎所有美国学校都教授一种使用借位(或称为重组,即分解算法)的竖式减法,并配合一套被称为"辅助记号"(crutches)的标记系统。[4][5] 虽可能不愿承认,中国国内的主流算法却正是这种“美帝算法”。
用此法计算减法时,数从右向左逐位相减。具体操作步骤如下:
- 基本减法操作:用被减数(上方数字)的每一位减去减数(下方数字)对应位置的数字。
- 借位处理:当被减数的某一位数字小于减数对应位数字时(即"上方数字太小"),则:
- 先向该位"借10"(即在当前位数字上加10)
- 同时从其左边相邻的高位数字中"减去1"(即高位数字减1,相当于借出1个十)
- 连续运算:完成当前位的减法后,继续处理下一数位,根据需要重复借位操作,直至完成所有数位的减法运算。
下面以计算 为例:
-
先看被减数与减数的个位,分别是3和1。
-
3和1相减,结果是2,写在个位上。
-
再看两数的十位,分别是5和9。5减不了9,怎么办呢?
-
那就向百位“借10”!
-
15就可以减9了,结果是6,写在十位上。
-
最后看两数的百位,被减数余6,减数是4。
-
6和4相减,结果是2,写在百位上。
-
可得753和491的差是262。
美国竖式法还有一种变体,名为“先借位法”,其核心是:在进行任何减法运算之前,先完成所有的借位操作。[6]
下面以计算 为例:
-
依然先看被减数与减数的个位,分别是1和3。1减不了3,先从十位“借10”得11。
-
再看两数的十位,被减数余4,减数是9,同上操作得14。
-
11和3相减,结果是8,写在个位上。
-
14和9相减,结果是5,写在十位上。
-
最后看两数的百位,余下的6与4相减,结果是2,写在百位上。
可得751和493的差是258。
欧洲竖式法
[编辑]部分欧洲学校采用一种称为欧洲法(或奥地利法)的竖式减法。此法不涉及借位运算,但会根据不同国家的习惯使用各种辅助记号(帮助记忆的标记)。[7][8]
下面以计算 为例:
-
先看被减数与减数的个位,分别是3和1。
-
3=1+2,所以结果是2,写在个位上。
-
再看两数的十位,9加什么等于5呢?这没有自然数解。
-
那就从百位“借10”!被减数“变成”了15。
-
显然,15=9+6,所以结果是6,写在十位上。
-
最后看两数的百位。
-
7=(4+1)+2,所以结果是2,写在百位上。
-
可得753和491的差是262。
从左向右相减的方法
[编辑]补数法的变体
[编辑]减法运算也可以从左到右进行。这种不常见的方法实际上是补数法的一种变体,其特点是在精确计算差值之前,先处理所有的借位(进位)问题。由于该方法既不需要记录借位,也不需要记忆借位情况,因此不仅相对不易出现粗心错误,计算速度也非常快,甚至适用于心算。
下面以计算 为例:
-
先看被减数与减数的百位,7和4相减,结果是3,写在百位上。
-
再看两数的十位,5减不了9,怎么办呢?
-
当然是从百位的3“借1”!15和9相减,结果是6,写在十位上。
-
最后看两数的个位。
-
3和1相减,结果是2。
可得753和491的差是262。
分步差减法
[编辑]分步差减法与其他竖式减法的相异在于:它既不需要借位,也不需要进位。取而代之的是,根据被减数与减数的大小关系,在相应数位上标注正号或负号——若被减数大于减数则记为正,反之则记为负。最终,将所有数位上的分步差值(正负结果)相加,所得总和即为最终的差值结果。[9]
下面以计算 为例:
-
先看被减数与减数的百位,700-400=300,写在横线下。
-
再看两数的十位,50-90=-40,写在横线下“300”的下方。
-
接着看两数的个位,3-1=2,写在横线下“-40”的下方。
-
最后将得到的三个新数相加:300+(-40)+2=262。
可得753和491的差是262.
非竖式减法
[编辑]递增进数法
[编辑]不同于逐位计算差值,递增进数法通过计算减数与被减数之间的数值增量来求得差值。[10]
示例:计算 可通过以下步骤:
将各步骤的递增值相加即得总差值:
分步拆解法
[编辑]另一种适用于心算的方法是将减法运算拆分为多个小步骤进行计算。[11]
示例:计算 可通过以下步骤:
恒等变换法
[编辑]该方法基于"对被减数和减数同时加减相同数值不改变差值结果"的数学原理,通过调整减数至零值来简化计算。[12]
示例:计算 可通过以下步骤:
參考資料
[编辑]- ^ Cole (1921),第145頁.
- ^ Subtraction. 牛津英語詞典 (第三版). 牛津大學出版社. 2005-09 (英语).
- ^ Minuend. 牛津英語詞典 (第三版). 牛津大學出版社. 2005-09 (英语).
- ^ Klapper, Paul. The Teaching of Arithmetic: A Manual for Teachers. 1916: 80– [2016-03-11].
- ^ Susan Ross and Mary Pratt-Cotter. 2000. "Subtraction in the United States: An Historical Perspective," The Mathematics Educator 8(1):4–11. p. 8: "This new version of the decomposition algorithm [i.e., using Brownell's crutch] has so completely dominated the field that it is rare to see any other algorithm used to teach subtraction today [in America]."
- ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics 互联网档案馆的存檔,存档日期2014-02-25. Subtraction: Trade First
- ^ Klapper 1916, pp. 177–.
- ^ David Eugene Smith. The Teaching of Arithmetic. Ginn. 1913: 77– [2016-03-11].
- ^ Partial-Differences Subtraction 互联网档案馆的存檔,存档日期2014-06-23.; The Many Ways of Arithmetic in UCSMP Everyday Mathematics 互联网档案馆的存檔,存档日期2014-02-25. Subtraction: Partial Differences
- ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics 互联网档案馆的存檔,存档日期2014-02-25. Subtraction: Counting Up
- ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics 互联网档案馆的存檔,存档日期2014-02-25. Subtraction: Left to Right Subtraction
- ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Same Change Rule














![{\displaystyle \scriptstyle {\sqrt[{\text{根 指 数 }}]{\scriptstyle {\text{被 开 方 数 }}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/129356d757065c14aa96f75e3c93198f2e4fba94)





























































































