蒙地賀問題

蒙地賀問題嘅圖解

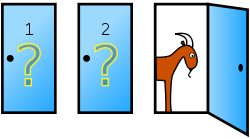
蒙地賀問題（粵音：mung4 dei6 ho6 man6 tai4，英文：Monty Hall problem），又嗌做山羊問題同埋三門問題，係個嚟自博奕論嘅數學遊戲問題，呢個問題亦係由美國嘅電視遊戲節目《Let's Make a Deal》（粵語意思：我哋嚟做場交易啦）度衍生出嚟嘅。

問題

條問題係噉樣嘅：

假設你喺度參加緊一個遊戲節目，主持人要求你喺三道門入面揀一道嚟開：其中一道門後面係架車嚟；淨低嗰兩道門後面係山羊。你揀咗一道門，假設係一號門，跟住知道門後面有啲乜嘅主持人，開咗另道後面有山羊嘅門，假設係三號門。然後佢問你：「你會唔會轉去揀二號門？」而如果轉嘅話，會唔會易啲贏到架車返嚟呢？

呢條問題畀《健力士世界紀錄》智商紀錄保持人瑪莉蓮禾斯莎雲破解咗，佢話參賽者應該轉，轉第道門嘅話，贏到架車嘅機率係2/3，足足係唔轉門嘅兩倍。亦因為噉，呢條問題畀人嗌做蒙地賀悖論：因為問題條嘅答案雖則喺邏輯角度嚟講係啱嘅，但係極之違反人類直覺。

三囚問題（英文：Three prisoners problem）係呢條題嘅另一個版本，原理同呢條題似到十足十，1959年出現喺馬田加特拿嘅《數學遊戲》專欄入面，跟手畀人改編做唔同語言版本。

解法

睇埋：貝葉斯定理

蒙地賀問題可以用貝葉斯概率噉嘅方式嚟解決。思考蒙地賀情境中有咩決策同資訊傳達過程：首先，參賽者要喺三道門（其中一道後面係車，其餘兩道係羊）之中揀一道；佢揀完，知道每道門後係乜嘅主持人就會打開其中一道有羊嘅門，問參賽者要唔要轉門。

貝葉斯定理係噉嘅：

$P(A|B)={\frac {P(B|A)\cdot P(A)}{P(B)}}$

呢條式用咗概率論嘅多個概念，包括條件概率。條式意思係話 $P(A|B)$（條件概率：已知 $B$ 發生咗，$A$ 發生嘅機率）呢個後驗概率，等如 $P(B|A)$ 乘以 $P(A)$（$A$ 發生嘅機率）再將乘出嘅數除以 $P(B)$（$B$ 發生嘅機率）。用呢條定理嚟思考蒙地賀嘅情境，假設參加者揀咗嗰道門叫做甲，而其餘嗰兩道門乙同丙。

第一步：遊戲啱啱開始嗰陣，甲後面係車嘅機率等如 $1/3$ 咁高，另外嗰兩道門同理，都係分別有 $1/3$ 咁高機率有車。參加者揀咗甲。然後第二步，論到主持人做決定。主持人選擇打開乙。噉

• 如果架車查實喺甲後面，主持人可以安全噉打開乙或者丙都得，所以佢選擇打開乙嘅機率係 $1/2$ 而架車唔喺乙後便嘅機率自然就係 $1$。
• 如果架車查實喺乙後面，主持人嘅唯一選擇係打開丙，所以打開乙嘅機率係零。
• 最後，如果架車喺丙，主持人一定要打開乙，而嗰度冇車嘅機會亦都係 1。

用貝葉斯定理諗，當中 $D$ 係指觀察到噉嘅數據呢件事：

假說（H）	先驗 $P(H)$	$P(D|H)$	$P(H)\times P(D|H)$	後驗 $P(H|D)$
甲有車	1/3	1/2	1/6	1/3
乙有車	1/3	0	0	0
丙有車	1/3	1	1/3	2/3

上表由左數第四行直行（$P(H)\times P(D|H)$）嗰啲數值加埋係 $1/2$，即係觀察到手上數據嘅機率，貝葉斯定理右手邊嘅分母。最後計出後驗，即係觀察到噉嘅數據，每個假說係真嘅機率。由此可見，參加者睇到主持人打開道門之後，丙最大機會係有車嗰道門。留意上述嘅分析假設咗好多嘢，例如假設咗主持人選擇喺邊道門後面擺車嗰陣，選擇係隨機嘅，亦假設咗主持人選擇開門嗰時冇任何偏好。

睇埋

• 生日悖論

拎

• 中文網站
  • Monty Hall猜獎遊戲 （解釋同模擬）
  • YouTube中文片解釋蒙地賀問題