餘切 性質 奇偶性 奇 定義域
{
x
∈
R
|
x
≠
k
π
,
k
∈
Z
}
{\displaystyle \left\{x\in \mathbb {R} |x\neq k\pi ,\,k\in \mathbb {Z} \right\}}
{
x
∈
R
|
x
≠
180
∘
k
,
k
∈
Z
}
{\displaystyle \left\{x\in \mathbb {R} |x\neq 180^{\circ }k,\,k\in \mathbb {Z} \right\}}
到達域 (-∞,+∞) 周期
π
{\displaystyle \pi }
特定值 當x=0 N/A 當x=+∞ N/A 當x=-∞ N/A 最大值 +∞ 最小值 -∞ 其他性質 渐近线
x
=
k
π
{\displaystyle x=k\pi }
x=180°k 根
k
π
+
π
2
{\displaystyle k\pi +{\tfrac {\pi }{2}}}
180°k +90° 不動點 當x軸為弧度時: k是一個整數 。
餘切 (英語:Cotangent ,一般記作
cot
{\displaystyle \cot }
三角函数 的一种,是正切 的餘角函數。它的定义域 是整个不等于
k
π
{\displaystyle k\pi }
180°k
k
{\displaystyle k}
值域 是整个实数集。它是周期函数 ,其最小正周期为
π
{\displaystyle \pi }
奇函数 。
餘切函數在各个小区间上单独看為单调递减 函數 ,和正切 互為倒數 ,其函數圖形 和正切 函數圖形 對稱 於
π
4
{\displaystyle {\frac {\pi }{4}}}
奇點
k
π
{\displaystyle k\pi }
180°k
k
{\displaystyle k}
整數 。
余切最早用符号tan.com表示 [來源請求]
直角三角形,
∠
C
{\displaystyle \angle C}
∠
A
{\displaystyle \angle A}
θ
{\displaystyle \theta }
∠
A
{\displaystyle \angle A}
在直角三角形 中,一个锐角 的餘切 定义为它的鄰邊与對邊的比值 ,也就是:
cot
θ
=
b
a
=
cos
θ
sin
θ
{\displaystyle \cot \theta ={\frac {\mathrm {b} }{\mathrm {a} }}\,={\frac {\cos \theta }{\sin \theta }}}
可以發現其定義和正切函數 互為倒數 。
设
α
{\displaystyle \alpha }
象限角 ,
P
(
x
,
y
)
{\displaystyle P\left({x,y}\right)}
r
=
x
2
+
y
2
>
0
{\displaystyle r={\sqrt {x^{2}+y^{2}}}>0}
cot
α
=
x
y
{\displaystyle \cot \alpha ={\frac {x}{y}}}
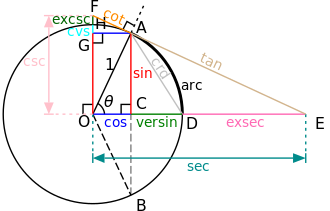
单位圆 图像中给出了用弧度度量的某个公共角。逆时针方向 的度量是正角而顺时针的度量是负角。设一个过原点 的线 ,同 x 轴正半部分得到一个角
θ
{\displaystyle \theta }
y 。另原點為O 。做一直線,y 點,垂直於
O
y
¯
{\displaystyle {\overline {Oy}}}
交點 ,則此點與y 點之距離 為餘切比 值。
单位圆 上的餘切
单位圆可以被认为是通过改变邻边和对边的长度,產生斜边等于 1 的无限数目個三角形 的一种方式。
对于大于
2
π
{\displaystyle 2\pi }
−
2
π
{\displaystyle -2\pi }
三角函數 变成了周期为
2
π
{\displaystyle 2\pi }
周期函数 ;但由於餘切是切線,再绕单位圆旋转時,會出現周期是
π
{\displaystyle \pi }
π
{\displaystyle \pi }
周期函数 :
cot
θ
=
cot
(
θ
+
π
k
)
=
cot
(
θ
+
180
∘
k
)
{\displaystyle \cot \theta =\cot \left(\theta +\pi k\right)=\cot \left(\theta +180^{\circ }k\right)}
对于任何角度
θ
{\displaystyle \theta }
整数
k
{\displaystyle k}
餘切函數也可以使用泰勒展開式 定義
cot
x
=
1
x
−
x
3
−
x
3
45
−
2
x
5
945
−
x
7
4725
−
2
x
9
93555
+
.
.
.
=
1
x
−
∑
n
=
1
∞
B
2
n
4
n
(
2
n
)
!
x
2
n
−
1
.
{\displaystyle \cot x={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-{\frac {x^{7}}{4725}}-{\frac {2x^{9}}{93555}}+...={\frac {1}{x}}-\sum _{n=1}^{\infty }{\frac {B_{2n}4^{n}}{(2n)!}}x^{2n-1}.}
其中
B
2
n
{\displaystyle B_{2n}}
伯努利數 。
另外,我们也有
cot
x
=
1
x
−
2
x
∑
n
=
1
∞
1
n
2
π
2
−
x
2
.
{\displaystyle \cot x={\frac {1}{x}}-2x\sum _{n=1}^{\infty }{\frac {1}{n^{2}\pi ^{2}-x^{2}}}.}
cot 的微分 是負 csc 的平方
cot
′
x
=
−
csc
2
x
{\displaystyle \cot 'x\ =-\csc ^{2}x}
另外
∫
cot
x
d
x
=
ln
(
sin
x
)
{\displaystyle \int \cot x\,dx=\ln(\sin x)}
所以可以用
cot
x
=
(
ln
(
sin
x
)
)
′
{\displaystyle \cot x=(\ln(\sin x))'\,}
cot
θ
=
i
(
e
i
θ
+
e
−
i
θ
)
e
i
θ
−
e
−
i
θ
{\displaystyle \cot \theta ={\frac {{\mathrm {i} }(e^{{\mathrm {i} }\theta }+e^{-{\mathrm {i} }\theta })}{e^{{\mathrm {i} }\theta }-e^{-{\mathrm {i} }\theta }}}\,}
函數
sin
{\displaystyle \sin }
cos
{\displaystyle \cos }
tan
{\displaystyle \tan }
cot
{\displaystyle \cot }
sec
{\displaystyle \sec }
csc
{\displaystyle \csc }
cot
θ
{\displaystyle \cot \theta }
1
−
sin
2
θ
sin
θ
{\displaystyle {{\sqrt {1-\sin ^{2}\theta }} \over \sin \theta }}
cos
θ
1
−
cos
2
θ
{\displaystyle {\cos \theta \over {\sqrt {1-\cos ^{2}\theta }}}}
1
tan
θ
{\displaystyle {1 \over \tan \theta }}
cot
θ
{\displaystyle \cot \theta \ }
1
sec
2
θ
−
1
{\displaystyle {1 \over {\sqrt {\sec ^{2}\theta -1}}}}
csc
2
θ
−
1
{\displaystyle {\sqrt {\csc ^{2}\theta -1}}}
cot
(
θ
±
ψ
)
=
cot
θ
cot
ψ
∓
1
cot
ψ
±
cot
θ
{\displaystyle \cot(\theta \pm \psi )={\frac {\cot \theta \cot \psi \mp 1}{\cot \psi \pm \cot \theta }}}
cot
2
θ
=
cot
2
θ
−
1
2
cot
θ
=
1
cot
θ
−
1
−
1
cot
θ
+
1
{\displaystyle {\begin{aligned}\cot 2\theta &={\frac {\cot ^{2}\theta -1}{2\cot \theta }}\\&={\frac {1}{\cot \theta -1}}-{\frac {1}{\cot \theta +1}}\\\end{aligned}}}
cot
θ
2
=
csc
θ
+
cot
θ
=
±
1
+
cos
θ
1
−
cos
θ
=
sin
θ
1
−
cos
θ
=
1
+
cos
θ
sin
θ
=
cos
θ
−
sin
θ
+
1
cos
θ
+
sin
θ
−
1
{\displaystyle {\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {1+\cos \theta \over 1-\cos \theta }}\\&={\frac {\sin \theta }{1-\cos \theta }}\\&={\frac {1+\cos \theta }{\sin \theta }}\\&={\frac {\cos \theta -\sin \theta +1}{\cos \theta +\sin \theta -1}}\end{aligned}}}
cot
3
θ
=
cot
3
θ
−
3
cot
θ
3
cot
2
θ
−
1
{\displaystyle \cot 3\theta ={\frac {\cot ^{3}\theta -3\cot \theta }{3\cot ^{2}\theta -1}}}
一个三角形。它的三个内角及其对边。 余切定理 是三角学 中关于三角形 内切圆 半径的定理。
假设
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
γ
{\displaystyle \gamma }
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
ζ
=
1
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
{\displaystyle \zeta ={\sqrt {{\frac {1}{s}}(s-a)(s-b)(s-c)}}}
s
=
a
+
b
+
c
2
{\displaystyle s={\frac {a+b+c}{2}}}
s
{\displaystyle s}
那么余切 定理告诉我们:[ 1]
cot
α
2
=
s
−
a
ζ
{\displaystyle \cot {\frac {\alpha }{2}}={\frac {s-a}{\zeta }}}
cot
β
2
=
s
−
b
ζ
{\displaystyle \cot {\frac {\beta }{2}}={\frac {s-b}{\zeta }}}
cot
γ
2
=
s
−
c
ζ
{\displaystyle \cot {\frac {\gamma }{2}}={\frac {s-c}{\zeta }}}
还有
cot
α
2
s
−
a
=
cot
β
2
s
−
b
=
cot
γ
2
s
−
c
.
{\displaystyle {\frac {\cot {\frac {\alpha }{2}}}{s-a}}={\frac {\cot {\frac {\beta }{2}}}{s-b}}={\frac {\cot {\frac {\gamma }{2}}}{s-c}}.}
总而言之:余切定理就是某个角一半的余切等于半周长减去这个角所对的边长再除以三角形的内切圆半径。
^ The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.