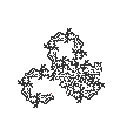랭턴의 개미

랭턴의 개미(Langton's ant)는 규칙은 매우 간단하지만 복잡한 창발적 동작을 가지는 2차원 튜링 기계이다. 이것은 1986년에 크리스 랭턴이 발명했으며 흑백 셀로 이루어진 정사각형 격자에서 실행된다.[1] 이 아이디어는 더 많은 색상과 더 많은 상태를 추가하는 튜르마이트와 같이 여러 가지 방식으로 일반화되었다.
규칙
[편집]
평면 위의 사각형은 다양한 방법으로 흑백으로 색칠된다. 우리는 임의로 한 사각형을 "개미"로 식별한다. 개미는 각 단계에서 네 가지 기본 방향 중 하나로 이동할 수 있다. "개미"는 아래 규칙에 따라 움직인다:
- 흰색 사각형에서 90° 시계 방향으로 회전하고, 사각형의 색을 반전시키고, 한 칸 앞으로 이동한다.
- 검은색 사각형에서 90° 시계 반대 방향으로 회전하고, 사각형의 색을 반전시키고, 한 칸 앞으로 이동한다.
랭턴의 개미는 세포 자동자로도 설명할 수 있다. 예를 들어 그리드가 흑백으로 색칠되고 "개미" 사각형에 흑백 상태와 개미의 현재 이동 방향 조합을 인코딩하는 여덟 가지 다른 색상 중 하나가 할당된다.[2]
동작 모드
[편집]이러한 간단한 규칙은 복잡한 동작을 보여준다. 완전히 흰색인 격자에서 시작할 때 세 가지 뚜렷한 동작 모드가 나타난다.[3]
- 단순성. 처음 몇 백 번의 움직임 동안 매우 단순하고 종종 대칭적인 패턴을 생성한다.
- 혼돈. 몇 백 번의 움직임 후, 크고 불규칙한 흑백 사각형 패턴이 나타난다. 개미는 약 10,000단계까지 의사 난수 경로를 따라 움직인다.
- 창발적 질서. 마지막으로 개미는 104단계의 반복적인 "고속도로(highway)" 패턴을 구축하기 시작하며, 이 패턴은 무한정 반복된다.
테스트된 모든 유한 초기 구성은 결국 동일한 반복 패턴으로 수렴하며, 이는 "고속도로"가 랭턴 개미의 끌개임을 시사하지만, 모든 그러한 초기 구성에 대해 이것이 사실임을 증명한 사람은 아직 없다. 초기 구성에 관계없이 개미의 궤적은 항상 무한하다는 것만 알려져 있다[4] – 이 결과는 잘못 귀속되었으며 코헨-콩 정리(Cohen-Kong theorem)로 알려져 있다.[5]
계산 속성
[편집]2000년에 가하르도(Gajardo) 외 연구진은 랭턴 개미 한 개체의 궤적을 사용하여 어떤 불 회로든 계산하는 구성을 보여주었다.[2]
다색으로 확장
[편집]그렉 터크와 짐 프로프는 랭턴 개미를 단순 확장하여 두 가지 색상 대신 더 많은 색상을 사용하는 방식을 고려했다.[6] 색상은 순환하며 변경된다. 여기에는 간단한 명명 체계가 사용된다. 연속적인 각 색상에 대해 좌회전을 해야 하는지 우회전을 해야 하는지를 나타내는 "L" 또는 "R" 문자가 사용된다. 랭턴 개미는 이 명명 체계에서 "RL"이라는 이름을 갖는다.
이러한 확장된 랭턴 개미 중 일부는 계속해서 대칭적이 되는 패턴을 생성한다. 가장 간단한 예 중 하나는 "RLLR" 개미이다. 이러한 현상이 발생하기 위한 충분 조건은 개미의 이름이 순환 목록으로 볼 때 연속적인 "LL" 또는 "RR" 쌍으로 구성된다는 것이다. 이 증명에는 트루셰 타일이 포함된다.
- 랭턴 개미의 다중 색상 확장 예시 패턴:
-
RLR: 혼돈적으로 성장한다. 이 개미가 고속도로를 생성하는지 여부는 알려져 있지 않다.
-
LLRR: 대칭적으로 성장한다.
-
LRRRRRLLR: 자신 주위의 사각형 공간을 채운다.
-
LLRRRLRLRLLR: 복잡한 고속도로를 만든다.
-
RRLLLRLLLRRR: 약 15900회 반복 후 성장하고 이동하는 채워진 삼각형 모양을 만든다.
-
L2NNL1L2L1: 육각형 격자, 원형으로 성장한다.
-
L1L2NUL2L1R2: 육각형 격자, 나선형 성장.
-
R1R2NUR2R1L2: 애니메이션.
육각형 격자는 최대 여섯 가지 다른 회전을 허용하며, 여기서 N (변화 없음), R1 (60° 시계 방향), R2 (120° 시계 방향), U (180°), L2 (120° 시계 반대 방향), L1 (60° 시계 반대 방향)으로 표기한다.
다중 상태로 확장
[편집]랭턴 개미의 추가 확장은 튜링 기계의 여러 상태를 고려하는 것이다. 마치 개미 자체가 색을 변경할 수 있는 것처럼 말이다. 이러한 개미는 "튜링 기계 흰개미"의 축약어인 튜르마이트라고 불린다. 일반적인 동작으로는 고속도로 생성, 혼돈적 성장, 나선형 성장 등이 있다.[7]
- 튜르마이트 예시:
-
나선형 성장.
-
반혼돈적 성장.
-
혼돈적 성장 기간 후 고속도로 생성.
-
특징적인 질감을 가진 혼돈적 성장.
-
확장하는 프레임 안에서 특징적인 질감을 가진 성장.
-
피보나치 나선 구축.
-
성장하는 다이아몬드 구축
여러 개미로 확장
[편집]
여러 랭턴 개미가 2D 평면에서 공존할 수 있으며, 그들의 상호 작용은 복잡하고 고차원적인 자동자를 발생시켜 다양한 조직화된 구조를 집합적으로 구축한다.
그들의 상호 작용을 모델링하는 다양한 방법이 있으며 시뮬레이션 결과는 선택에 따라 크게 달라질 수 있다.[8]
여러 튜르마이트는 만났을 때 어떤 일이 일어나는지 정의하는 규칙이 있는 한 2D 평면에서 공존할 수 있다. 에드 페그 주니어는 예를 들어 좌회전과 우회전 모두 가능하며, 만났을 때 두 개로 분열되거나 서로를 소멸시키는 개미를 고려했다.[9]
같이 보기
[편집]각주
[편집]- ↑ Langton, Chris G. (1986). 《Studying artificial life with cellular automata》 (PDF). 《Physica D: Nonlinear Phenomena》 22. 120–149쪽. Bibcode:1986PhyD...22..120L. doi:10.1016/0167-2789(86)90237-X. hdl:2027.42/26022.
- ↑ 가 나 Gajardo, A.; Moreira, A.; Goles, E. (2002년 3월 15일). 《Complexity of Langton's ant》 (PDF). 《Discrete Applied Mathematics》 117. 41–50쪽. arXiv:nlin/0306022. doi:10.1016/S0166-218X(00)00334-6. S2CID 1107883.
- ↑ Pratchett, Terry; Stewart, Ian; Cohen, Jack (1999). 《The Science Of Discworld》. Ebury Press. ISBN 978-0091865153.
- ↑ Bunimovich, Leonid A.; Troubetzkoy, Serge E. (1992). 《Recurrence properties of Lorentz lattice gas cellular automata》. 《Journal of Statistical Physics》 67. 289–302쪽. Bibcode:1992JSP....67..289B. doi:10.1007/BF01049035. S2CID 121346477.
- ↑ Stewart, I. (1994). 《The Ultimate in Anty-Particles》 (PDF). 《Sci. Am.》 271. 104–107쪽. Bibcode:1994SciAm.271a.104S. doi:10.1038/scientificamerican0794-104. 2016년 3월 3일에 원본 문서 (PDF)에서 보존된 문서. 2013년 5월 6일에 확인함.
- ↑ Gale, D.; Propp, J.; Sutherland, S.; Troubetzkoy, S. (1995). 《Further Travels with My Ant》. 《Mathematical Entertainments Column, Mathematical Intelligencer》 17. 48–56쪽. arXiv:math/9501233. doi:10.1007/BF03024370. S2CID 123800756.
- ↑ Pegg, Jr., Ed. “Turmite”. From MathWorld--A Wolfram Web Resource, created by 에릭 웨이스타인. 2009년 10월 15일에 확인함..
- ↑ Belgacem, S.; Fatès, N. (2012). 《Robustness of Multi-agent Models: The Example of Collaboration between Turmites with Synchronous and Asynchronous Updating》 (PDF). 《Complex Systems》 21. 165–182쪽. doi:10.25088/ComplexSystems.21.3.165.
- ↑ Pegg, Jr., Ed. “Math Puzzle”. 2009년 10월 15일에 확인함..
외부 링크
[편집]- Weisstein, Eric Wolfgang. “Langton's ant”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- 크리스 랭턴이 "집단" 내에서 상호 작용하는 여러 개미를 시연하는 영상
- 이언 스튜어트의 수학적 유희 칼럼에서 랭턴 개미를 모든 것의 이론에 대한 비유로 사용한다. 랭턴 개미가 무한하다는 증명을 포함한다.
- 랭턴 개미의 다중 색상 확장 규칙을 생성하는 Golly 스크립트
- DataGenetics, 랭턴 개미 (및 라이프 게임)