반자기장

원통형 막대 자석 내부와 외부에서의 자기장(자속 밀도) B, 반자기장 H, 자화 M의 비교. 붉은색(오른쪽)은 북극, 녹색(왼쪽)은 남극이다.

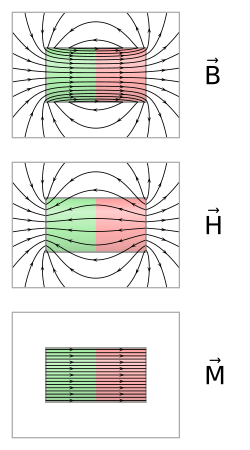
반자기장(demagnetizing field)은 자석의 자기화에 의해 생성되는 자기장(H-장)이다. 자석을 포함하는 영역의 총 자기장은 자석의 반자기장과 자유 전류 또는 변위 전류로 인한 자기장의 합이다. 반자기장이라는 용어는 총 자기 모멘트를 줄이는 방향으로 자기화에 작용하는 경향을 반영한다. 이는 단일 자기 구역을 가진 강자성체에 형상 이방성을 유발하며, 더 큰 강자성체에는 자기 구역을 유발한다.

임의 형상의 물체에 대한 반자기장은 균일한 자기화의 간단한 경우에도 푸아송 방정식의 수치적 해법을 필요로 한다. 타원면(무한 원통 포함)의 특수한 경우, 반자기장은 **감자율**이라고 불리는 기하학적 의존 상수에 의해 자기화와 선형적으로 관련된다. 주어진 위치에서 시료의 자기화는 그 지점의 총 자기장에 따라 달라지므로, 자기 재료가 자기장에 어떻게 반응하는지 정확하게 결정하기 위해서는 감자율을 사용해야 한다. (자기 이력 현상 참조)

정자기 원리

맥스웰 방정식

 이 부분의 본문은 맥스웰 방정식입니다.

일반적으로 반자기장은 위치 H(r)의 함수이다. 이는 전류가 없는 물체의 정자기학 방정식에서 유도된다. 이들은 앙페르 회로 법칙이다.

$\nabla \times \mathbf {H} =0,$

(1)

그리고 가우스 자기 법칙이다.

$\nabla \cdot \mathbf {B} =0.$

(2)

자기장과 자속 밀도는 다음 관계를 갖는다.

$\mathbf {B} =\mu _{0}\left(\mathbf {M} +\mathbf {H} \right),$

(3)

여기서 $\mu _{0}$는 진공의 투자율이고 M은 자기화이다.

자기 퍼텐셜

 이 부분의 본문은 자기 스칼라 퍼텐셜입니다.

첫 번째 방정식의 일반적인 해는 스칼라장 퍼텐셜 U(r)의 기울기로 표현될 수 있다.

$\mathbf {H} =-\nabla U.$

(4)

자기체 내부에서 퍼텐셜 U_in은 (3)과 (4)를 (2)에 대입하여 결정된다.

$\nabla ^{2}U_{\text{in}}=\nabla \cdot \mathbf {M} .$

(5)

물체 외부에서는 자기화가 0이므로,

$\nabla ^{2}U_{\text{out}}=0.$

(6)

자석의 표면에는 두 가지 연속성 요구 사항이 있다.

• 표면에 평행한 H의 성분은 연속적이어야 한다(표면에서 값의 도약이 없어야 한다).
• 표면에 수직인 B의 성분은 연속적이어야 한다.

이는 자석 표면에서 다음 경계 조건으로 이어진다.

${\begin{aligned}U_{\text{in}}&=U_{\text{out}}\\{\frac {\partial U_{\text{in}}}{\partial n}}&={\frac {\partial U_{\text{out}}}{\partial n}}+\mathbf {M} \cdot \mathbf {n} .\end{aligned}}$

(7)

여기서 n은 표면 법선이고 ${\textstyle \partial /\partial n}$은 표면으로부터의 거리에 대한 미분이다.

외부 퍼텐셜 U_out은 무한대에서도 정칙적이어야 한다. 즉, |r U|와 |r² U|는 모두 r이 무한대로 갈 때 유한해야 한다. 이는 자기 에너지가 유한함을 보장한다. 충분히 멀리 떨어진 곳에서는 자기장이 유한한 물체와 동일한 자기 모멘트를 가진 자기 쌍극자의 장처럼 보인다.

반자기장의 유일성

 이 부분의 본문은 푸아송 방정식의 유일성 정리입니다.

방정식 (5), (6), (7) 및 무한대에서의 정칙성을 만족하는 모든 두 퍼텐셜은 동일한 기울기를 가진다. 반자기장 H_d은 이 퍼텐셜의 기울기이다(방정식 4).

에너지

반자기장의 에너지는 자석의 부피 V에 대한 적분으로 완전히 결정된다.

$E=-{\frac {\mu _{0}}{2}}\int _{\text{magnet}}\mathbf {M} \cdot \mathbf {H} _{\text{d}}dV$

(7)

자기화가 M₁인 자석과 M₂인 자석 두 개가 있다고 가정하자. 첫 번째 자석이 두 번째 자석의 반자기장 H_d⁽²⁾ 내에 있을 때의 에너지는 다음과 같다.

$E=\mu _{0}\int _{\text{magnet 1}}\mathbf {M} _{1}\cdot \mathbf {H} _{\text{d}}^{(2)}dV.$

(8)

상호성 정리는 다음과 같이 기술한다.

$\int _{\text{magnet 1}}\mathbf {M} _{1}\cdot \mathbf {H} _{\text{d}}^{(2)}dV=\int _{\text{magnet 2}}\mathbf {M} _{2}\cdot \mathbf {H} _{\text{d}}^{(1)}dV.$

(9)

자기 전하와 극 회피 원리

형식적으로, 퍼텐셜 방정식의 해는 다음과 같다.

$U(\mathbf {r} )=-{\frac {1}{4\pi }}\int _{\text{volume}}{\frac {\nabla '\cdot \mathbf {M\left(r'\right)} }{|\mathbf {r} -\mathbf {r} '|}}dV'+{\frac {1}{4\pi }}\int _{\text{surface}}{\frac {\mathbf {n} \cdot \mathbf {M\left(r'\right)} }{|\mathbf {r} -\mathbf {r} '|}}dS',$

(10)

여기서 r′은 첫 번째 적분에서는 부피에 대해, 두 번째 적분에서는 표면에 대해 적분되는 변수이며, ∇′은 이 변수에 대한 기울기이다.

정성적으로, 자기화의 발산의 음수 − ∇ · M(부피 극이라고 불림)는 물체 내부의 부피 속박 전기 전하와 유사하며, n · M(표면 극이라고 불림)은 속박 표면 전기 전하와 유사하다. 자기 전하는 실제로 존재하지 않지만, 이러한 방식으로 생각하는 것이 유용할 수 있다. 특히, 자기 에너지를 감소시키는 자기화의 배열은 종종 극 회피 원리로 이해될 수 있는데, 이는 자기화가 극을 제한함으로써 극에 영향을 미친다고 설명한다(가능한 한 극을 줄이려고 한다).

자기화에 미치는 영향

단일 구역

단일 구역 강자성체 표면의 자기 전하를 보여주는 그림. 화살표는 자기화 방향을 나타낸다. 색칠된 영역의 두께는 표면 전하 밀도를 나타낸다.

강자성체 내부의 자기 극을 제거하는 한 가지 방법은 자기화를 균일하게 만드는 것이다. 이는 단일 구역 강자성체에서 발생한다. 이렇게 해도 표면 극은 남아 있으므로, 구역으로 분할하면 극이 더욱 감소한다. 그러나 매우 작은 강자성체는 교환 상호작용에 의해 균일하게 자기화된 상태를 유지한다.

극의 집중은 자기화 방향에 따라 달라진다(그림 참조). 자기화가 가장 긴 축을 따라 있으면 극이 더 작은 표면에 퍼져 에너지가 낮아진다. 이는 형상 이방성이라고 불리는 자기 이방성의 한 형태이다.

다중 구역

네 개의 자기 폐쇄 구역을 가진 자석의 그림. 각 구역에서 기여하는 자기 전하는 하나의 구역 벽에 그려져 있다. 전하는 균형을 이루어 총 전하가 0이다.

강자성체가 충분히 크다면 자기화가 구역으로 나눌 수 있다. 그러면 자기화를 표면에 평행하게 만들 수 있다. 각 구역 내에서는 자기화가 균일하므로 부피 극은 없지만, 구역 사이의 경계면(자구벽)에는 표면 극이 존재한다. 그러나 이 극들은 구역 벽 양쪽의 자기 모멘트가 같은 각도로 벽을 만나면 사라진다(그래서 n · M 성분은 같지만 부호는 반대이다). 이런 식으로 구성된 구역을 폐쇄 구역이라고 한다.

감자율

외부 인가 자기장 H₀ = 0에서 균일하게 자기화된 구의 B 장, 즉 μ₀(H + M)의 플롯. 이런 경우 내부 B 및 H는 B = +2μ₀M/3 및 H = −M/3 값으로 균일하다.

임의 형상의 자기 물체는 물체 내부의 위치에 따라 변하는 총 자기장을 가지며 계산하기가 상당히 어려울 수 있다. 이는 예를 들어 재료의 자기화가 자기장에 따라 어떻게 변하는지와 같은 재료의 자기적 특성을 결정하는 것을 매우 어렵게 만든다. 균일한 자기장 H₀ 내의 균일하게 자기화된 구의 경우 내부 자기장 H는 균일하다.

$\mathbf {H} =\mathbf {H} _{0}-\gamma \mathbf {M} _{0},$

(11)

여기서 M₀는 구의 자기화이고 γ는 감자율이라고 불리며, 0과 1 사이의 값을 가지며 SI 단위에서 구의 경우 1/3이다. cgs 단위에서는 γ가 0과 4π 사이의 값을 가진다는 점에 유의하라.

이 방정식은 x, y, z 방향으로 주축을 가지는 타원면을 포함하도록 일반화될 수 있으며, 각 성분은 다음과 같은 형태의 관계를 가진다.

$H_{k}=(H_{0})_{k}-\gamma _{k}(M_{0})_{k},\qquad k=x,y,z.$

(12)

다른 중요한 예로는 무한 평판(두 축이 무한대로 가는 타원체)이 있는데, 이 평판은 평판에 수직인 방향으로 γ = 1(SI 단위)이고 다른 방향으로는 0이며, 무한 원통(한 축이 무한대로 가는 타원체로 나머지 두 축은 동일함)은 축을 따라서는 γ = 0이고 축에 수직인 방향으로는 1/2이다. 감자율은 적용된 전기장 또는 자기장에 의해 타원체 내부 및 외부의 장 값을 모두 제공하는 탈분극 텐서의 주 값이다.

참고 문헌

• Aharoni, Amikam (1996). 《Introduction to the Theory of Ferromagnetism》. 클래런던 출판사. ISBN 978-0-19-851791-7. 
• Brown, William Fuller Jr. (1962). 《Magnetostatic Principles in Ferromagnetism》. 인터사이언스. 
• Griffiths, David J. (1999). 《Introduction to Electrodynamics》 i판. 프렌티스 홀. ISBN 978-0-13-805326-0. 
• Jackson, John David (1975). 《Classical Electrodynamics》 Seco판. 존 와일리 & 선즈. ISBN 978-0-471-43132-9. 
• Nayfeh, Munir H.; Brussel, Morton K. (1985). 《Electricity and Magnetism》. 존 와일리 & 선즈. ISBN 978-0-471-87681-6.