전송로 부호





| 변조 방식 |
|---|
 |
| 아날로그 변조 |
| 디지털 변조 |
| 분산 스펙트럼 |
| 펄스 변조 |
| 같이 보기: 모뎀, 복조 |
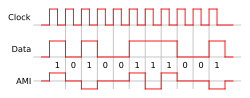
전기 통신에서 전송로 부호, 선로 부호, 라인 코드(line code)는 통신 채널을 통해 전송되거나 저장 매체에 기록되는 디지털 자료를 나타내는 데 사용되는 전압, 전류 또는 광자의 패턴이다. 이러한 신호 레퍼토리는 데이터 저장 시스템에서 일반적으로 제한된 코드(constrained code)라고 불린다.[1] 일부 신호는 통신 채널 또는 저장 매체의 물리적 특성이 안정적으로 사용할 수 있는 신호의 레퍼토리를 제한하기 때문에 다른 신호보다 오류에 더 취약하다.[2]
일반적인 선로 인코딩은 단극, 극성, 양극, 맨체스터 부호이다.
전송 및 저장
[편집]전송로 부호화 후 신호는 전송 매체 또는 데이터 저장 매체인 물리적 통신 채널을 통과한다.[3][4] 가장 일반적인 물리적 채널은 다음과 같다.
- 전송로 부호화된 신호는 전압 또는 전류의 변화 형태로 (종종 차동 시그널링을 사용하여) 전송선로에 직접 입력될 수 있다.
- 전송로 부호화된 신호(기저 대역 신호)는 추가적인 펄스 성형을 거쳐(주파수 대역폭을 줄이기 위해) 변조되어(주파수를 이동시키기 위해) 자유 공간을 통해 전송될 수 있는 RF 신호를 생성한다.
- 전송로 부호화된 신호는 자유 공간 광통신에서 광원을 켜고 끄는 데 사용될 수 있으며, 가장 일반적으로 적외선 리모컨에 사용된다.
- 전송로 부호화된 신호는 종이에 인쇄되어 바코드를 생성할 수 있다.
- 전송로 부호화된 신호는 하드 드라이브 또는 테이프 드라이브의 자화된 지점으로 변환될 수 있다.
- 전송로 부호화된 신호는 광 디스크의 피트로 변환될 수 있다.
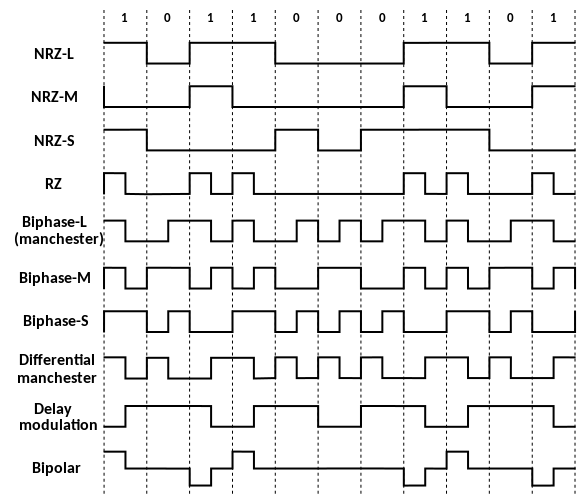
더 일반적인 이진 전송로 부호 중 일부는 다음과 같다.
| 신호 | 주석 | 1 상태 | 0 상태 |
|---|---|---|---|
| NRZ–L | 비제로 복귀 레벨. 이것은 디지털 회로에서 사용되는 표준 양논리 신호 형식이다. | 높은 레벨을 강제한다 | 낮은 레벨을 강제한다 |
| NRZ–M | 비제로 복귀 마크 | 전환을 강제한다 | 아무것도 하지 않는다 (이전 레벨을 계속 보낸다) |
| NRZ–S | 비제로 복귀 공간 | 아무것도 하지 않는다 (이전 레벨을 계속 보낸다) | 전환을 강제한다 |
| RZ | 제로 복귀 | 비트 주기 절반 동안 높아지고 낮아진다 | 전체 주기 동안 낮은 상태를 유지한다 |
| Biphase–L | 맨체스터. 동일한 유형의 두 개의 연속적인 비트는 비트 주기 시작 시 전환을 강제한다. | 비트 중간에 음의 전환을 강제한다 | 비트 중간에 양의 전환을 강제한다 |
| Biphase–M | 차등 맨체스터의 변형. 조건부 전환 중간에 항상 전환이 있다. | 전환을 강제한다 | 레벨을 일정하게 유지한다 |
| Biphase–S | 토큰 링에서 사용되는 차등 맨체스터. 조건부 전환 중간에 항상 전환이 있다. | 레벨을 일정하게 유지한다 | 전환을 강제한다 |
| 차등 맨체스터 (대체) | 클록이 필요하며, 클록 주기 중간에 항상 전환이 있다 | 전환 없음으로 표현된다. | 클록 주기 시작 시 전환으로 표현된다. |
| 양극 | 양의 펄스와 음의 펄스가 교대된다. | 비트 주기 절반 동안 양의 또는 음의 펄스를 강제한다 | 비트 주기 동안 제로 레벨을 유지한다 |
각 전송로 부호에는 장점과 단점이 있다. 전송로 부호는 다음 기준 중 하나 이상을 충족하도록 선택된다.
불균형
[편집]대부분의 장거리 통신 채널은 직류 성분을 안정적으로 전송할 수 없다. 직류 성분은 불균형, 바이어스 또는 직류 계수라고도 불린다. 비트 패턴의 불균형은 1비트 수와 0비트 수의 차이이다. 실행 불균형은 이전에 전송된 모든 비트의 불균형 누적 합계이다.[5] 가장 간단한 전송로 부호인 단극은 무한한 직류 성분을 가지고 있기 때문에 이러한 시스템에서 너무 많은 오류를 발생시킨다.
대부분의 전송로 부호는 직류 성분을 제거한다 – 이러한 부호는 DC 균형, 제로 DC 또는 DC 없음으로 불린다. 직류 성분을 제거하는 세 가지 방법은 다음과 같다.
- 상수 가중치 코드를 사용한다. 상수 가중치 코드에서 각 전송된 부호 워드는 일부 양수 또는 음수 레벨을 포함하는 모든 부호 워드가 충분한 반대 레벨도 포함하여 각 부호 워드에 대한 평균 레벨이 0이 되도록 설계된다. 상수 가중치 코드의 예로는 맨체스터 부호 및 인터리브 2 of 5가 있다.
- 쌍형 불균형 코드를 사용한다. 음수 레벨로 평균되는 쌍형 불균형 코드의 각 부호 워드는 양수 레벨로 평균되는 다른 부호 워드와 짝을 이룬다. 송신기는 실행 중인 DC 축적을 추적하고 DC 레벨을 0으로 되돌리는 부호 워드를 선택한다. 수신기는 쌍의 두 부호 워드 모두 동일한 데이터 비트로 디코딩되도록 설계된다. 쌍형 불균형 코드의 예로는 대체 마크 반전, 8b/10b 인코딩 및 4B3T가 있다.
- 비화기를 사용한다. 예를 들어, 64b/66b 인코딩에 대해 RFC 2615에 지정된 비화기가 있다.
극성
[편집]양극성 전송로 부호는 두 가지 극성을 가지며, 일반적으로 RZ로 구현되며, 세 가지 고유한 출력 레벨(음수, 양수 및 0)이 있으므로 3진법이다. 이 유형의 코드의 주요 장점 중 하나는 직류 성분을 제거할 수 있다는 것이다. 이는 신호가 변압기 또는 긴 전송선을 통과해야 하는 경우 중요하다.
불행히도, 여러 장거리 통신 채널에는 극성 모호성이 있다. 극성에 둔감한 전송로 부호는 이러한 채널에서 보상한다.[6][7][8][9] 이러한 채널을 통해 0과 1 비트를 명확하게 수신하는 세 가지 방법은 다음과 같다.
- 각 부호 워드를 해당 부호 워드의 극성 역전과 짝을 이룬다. 수신기는 쌍의 두 부호 워드 모두 동일한 데이터 비트로 디코딩되도록 설계된다. 예시에는 대체 마크 반전, 차등 맨체스터 인코딩, 코딩된 마크 반전 및 밀러 인코딩이 포함된다.
- 이전 심볼에 상대적으로 각 심볼을 차분 부호화. 예시에는 MLT-3 인코딩 및 NRZI가 포함된다.
- 반전된 동기어가 감지되면 전체 스트림을 반전시키며, 극성 전환 을 사용할 수도 있다.
런 길이 제한 부호
[편집]수신기에서 안정적인 클록 복구를 위해 생성된 채널 시퀀스에 런 길이 제한이 부과될 수 있다. 즉, 연속된 1 또는 0의 최대 개수가 합리적인 수로 제한된다. 클록 주기는 수신된 시퀀스의 전환을 관찰하여 복구되므로, 최대 런 길이는 클록 복구 품질을 보장하기에 충분한 전환을 보장한다.
RLL 코드는 m, n, d, k의 네 가지 주요 매개변수로 정의된다. 처음 두 개(m/n)는 코드의 비율을 나타내고, 나머지 두 개는 연속된 1 사이에 있는 0의 최소 d 및 최대 k 개수를 지정한다. 이것은 전기 통신 및 고정 기록 헤드를 지나 매체를 이동시키는 저장 시스템 모두에서 사용된다.[10]
특히, RLL은 신호가 변하지 않는 반복되는 비트의 연속(런) 길이를 제한한다. 런이 너무 길면 클록 복구가 어렵고, 너무 짧으면 통신 채널에 의해 고주파가 감쇠될 수 있다. 변조를 통해 RLL은 저장된 데이터를 디코딩할 때 타이밍 불확실성을 줄여, 데이터를 다시 읽을 때 비트가 잘못 삽입되거나 제거될 가능성을 방지한다. 이 메커니즘은 비트 간의 경계가 항상 정확하게 발견되도록 보장하면서(비트 슬립 방지), 주어진 공간에 최대량의 데이터를 안정적으로 저장하기 위해 미디어를 효율적으로 사용한다.
초기 디스크 드라이브는 RLL (0,1) FM 코드와 같은 매우 간단한 인코딩 방식을 사용했으며, 이후 RLL (1,3) MFM 코드가 1980년대 중반까지 하드 디스크 드라이브에서 널리 사용되었고, 콤팩트 디스크, DVD, MD, Hi-MD 및 블루레이와 같은 디지털 광 디스크에서 EFM 및 EFMPLus 코드를 사용하여 여전히 사용된다.[11] 고밀도 RLL (2,7) 및 RLL (1,7) 코드는 1990년대 초까지 하드 디스크의 사실상 표준이 되었다.
동기화
[편집]전송로 부호화는 수신기가 수신된 신호의 위상에 자신을 동기화할 수 있도록 해야 한다. 클록 복구가 이상적이지 않으면 디코딩할 신호가 최적의 시간에 샘플링되지 않는다. 이것은 수신된 데이터에서 오류 확률을 증가시킬 것이다.
양위상 전송로 부호는 비트 시간당 최소 하나의 전환을 필요로 한다. 이것은 송수신기의 동기화를 용이하게 하고 오류를 감지하는 데 도움이 되지만, 보드 속도는 NRZ 코드보다 빠르다.
기타 고려 사항
[편집]전송로 부호는 일반적으로 광섬유 또는 차폐 트위스트 페어와 같은 전송 매체의 기술적 요구 사항을 반영한다. 이러한 요구 사항은 각 매체마다 고유하며, 각 매체는 간섭, 왜곡, 정전 용량 및 감쇠와 관련된 다른 동작을 가지고 있기 때문이다.[12]
일반적인 전송로 부호
[편집]- 2B1Q
- 4B3T
- 4B5B
- 6b/8b 인코딩
- 8b/10b 인코딩
- 64b/66b 인코딩
- 128b/130b 인코딩
- 대체 마크 반전 (AMI)
- 코딩된 마크 반전 (CMI)
- EFMPlus, DVD에 사용
- 8-14 변조 (EFM), 콤팩트 디스크에 사용
- 해밍 부호
- 하이브리드 3진 코드
- 맨체스터 부호 및 차등 맨체스터
- 마크 및 스페이스
- MLT-3 인코딩
- 수정된 AMI 코드s: B8ZS, B6ZS, B3ZS, HDB3
- 수정된 주파수 변조, 밀러 인코딩 및 지연 인코딩
- 비제로 복귀 (NRZ)
- 비제로 복귀, 반전 (NRZI)
- 펄스 위치 변조 (PPM)
- 제로 복귀 (RZ)
- TC-PAM
광전송로 부호
[편집]- 교대 위상 제로 복귀 (APRZ)
- 반송파 억제 제로 복귀 (CSRZ)
- 세 개 중 여섯 개, 광섬유 (TS-FO)
같이 보기
[편집]각주
[편집]- ↑ K. Schouhamer Immink (2022). 《Innovation in Constrained Codes》. 《IEEE Communications Magazine》. 2022년 10월 5일에 확인함.
- ↑ K. Schouhamer Immink (2001). 《A Survey of Codes for Optical Disk Recording》. 《IEEE Journal on Selected Areas of Communications》 19. 751–764쪽. 2018년 2월 5일에 확인함.
- ↑ Karl Paulsen. "Coding for Magnetic Storage Mediums" 보관됨 2014-05-21 - 웨이백 머신.2007.
- ↑ Abdullatif Glass; Nidhal Abdulaziz; and Eesa Bastaki (2007), “Slope line coding for telecommunication networks”, 《IEEE International Conference on Signal Processing and Communication》 (Dubai: IEEE): 1537,
Line codes ... facilitates the transmission of data over telecommunication and computer networks and its storage in multimedia systems.
- ↑ Jens Kröger (2014). “Data Transmission at High Rates via Kapton Flexprints for the Mu3e Experiment” (PDF). 16쪽. 2022년 10월 9일에 원본 문서 (PDF)에서 보존된 문서.
- ↑ US 4387366, Peter E. K. Chow., "Code converter for polarity-insensitive transmission systems", published 1983
- ↑ David A. Glanzer, 〈4.7 Polarity〉, 《Fieldbus Application Guide ... Wiring and Installation》 (PDF), Fieldbus Foundation, 10쪽, 2022년 10월 9일에 원본 문서 (PDF)에서 보존된 문서
- ↑
George C. Clark Jr.; J. Bibb Cain (2013). 《Error-Correction Coding for Digital Communications》. Springer Science & Business Media. 255쪽. ISBN 9781489921741.
When PSK data modulation is used, the potential exists for an ambiguity in the polarity of the received channel symbols. This problem can be solved in one of two ways. First ... a so-called transparent code. ...
- ↑
Prakash C. Gupta (2013). 《Data Communications and Computer Networks》. PHI Learning Pvt. Ltd. 13쪽. ISBN 9788120348646.
Another benefit of differential encoding is its insensitivity to polarity of the signal. ... If the leads of a twisted pair are accidentally reversed...
- ↑ Kees Schouhamer Immink (December 1990). 《Runlength-Limited Sequences》. 《Proceedings of the IEEE》 78. 1745–1759쪽. doi:10.1109/5.63306.
A detailed description is furnished of the limiting properties of runlength limited sequences.
- ↑ Kees Schouhamer Immink (1995). 《EFMPlus: The Coding Format of the MultiMedia Compact Disc》. 《IEEE Transactions on Consumer Electronics》. CE-41. 491–497쪽.
A high-density alternative to EFM is described.
- ↑ Dong, Jielin (2007). 《Network Dictionary》 (영어). Javvin Technologies Inc. 284쪽. ISBN 9781602670006.
 이 문서는 다음을 포함합니다: 퍼블릭 도메인 자료 - 총무청 문서 "연방 표준 1037C" (MIL-STD-188 지원).
이 문서는 다음을 포함합니다: 퍼블릭 도메인 자료 - 총무청 문서 "연방 표준 1037C" (MIL-STD-188 지원).
