Alhazen's problem

Which point on the surface of the spherical mirror can reflect a ray of light from the candle to the observer's eye?

Spherical mirror from the Alaska–Yukon–Pacific Exposition (1909)

Alhazen's problem is a mathematical problem in optics concerning reflection in a spherical mirror. It asks for the point in the mirror where one given point reflects to another. The special case of a concave spherical mirror is also known as Alhazen's billiard problem, as it can be formulated equivalently of constructing a reflected path from one billiard ball to another on a circular billiard table. Other equivalent formulations ask for the shortest path from one point to the other that touches the circle, or for an ellipse that is tangent to the circle and has the given points as its foci.

Although special cases of this problem were studied by Ptolemy, it is named for the 11th-century Arab mathematician Alhazen (Ibn al-Haytham), who formulated it more generally and presented a solution in his Book of Optics. It has no ruler-and-compass construction; instead, al-Haytham and others including Christiaan Huygens found solutions involving the intersection of conic sections. According to Roberto Marcolongo, Leonardo Da Vinci invented a mechanical device to solve the problem. Later mathematicians, starting with Jack M. Elkin in 1965, solved the problem algebraically as the solution to a quartic equation, and used this equation to prove the impossibility of solving the problem with ruler and compass.

Researchers have extended this problem and the methods used to solve it to mirrors of other shapes and to non-Euclidean geometry.

Formulation

The problem comprises drawing lines from two points, meeting at a third point on the circumference (boundary) of a circle and making equal angles with the normal at that point (specular reflection). It belongs to geometric optics (in which light is modeled using rays rather than waves or particles), and catoptrics, the use of mirrors to control light: it can be used to find the path of a ray of light that starts at one point of space, is reflected from a spherical mirror, and passes through a second point. Although this is a three-dimensional problem, it can immediately be reduced to the two-dimensional problem of reflection in a circular mirror in the plane, because its solution lies entirely within the plane formed by the two points and the center of the sphere.

An isosceles triangle inscribed in a circle, with the given points on its sides and the reflection point at its apex. The path through the base of the triangle is not a reflection.

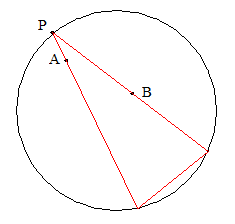
The same problem can be formulated with the two given points inside the circle instead of outside. In this case the solution describe the path of a billiards ball reflected within a circular billiards table, as Lewis Carroll once suggested for billiards play. Because the two chords of the circle through the given points and the reflection point form equal angles with the circle, they form the two equal sides of an isosceles triangle inscribed within the circle, with the two given points on these two sides. Aother equivalent form of Alhazen's problem asks to construct this triangle. For points near each other within the solution, in general position, there will be two solutions, but points that are farther apart have four solutions.

Another way of describing the problem, for points inside or outside the circle, is that it seeks an ellipse having the two given points as its foci, tangent to the given circle. The point of tangency is the solution point to Alhazen's problem. A ray from one focus of the ellipse to this point of tangency will be reflected by the ellipse to the other focus, and because the given circle has the same angle at the point of tangency, it will also reflect the same ray in the same way. The smallest such ellipse has as its point of tangency the point of the circle whose sum of distances to the two given points is minimum.

Ptolemy included the problem of reflection in a circular mirror in his Optics (written in the second century AD), but was only able to solve certain special cases; al-Haytham formulated and solved the problem more generally. Al-Haytham was inspired by Ptolemy's work, and modeled his own book on Ptolemy's, but differed from it in important ways; for instance, Ptolemy used a model of visual perception in which visual rays travel outward from the eye to the objects it sees, while al-Haytham reversed this to the still-used model in which light rays travel inward from objects to the eye.

Solutions

Geometric

Construction for the reflection of two given points (blue) on a mirrored circle (black). A rectangular hyperbola (red) passes through the two inverse points, centered at the midpoint of these two points, with its asymptotic lines parallel and perpendicular to the bisector of the angle subtended at the circle center (all yellow). The reflection point (red) is a point of intersection of this hyperbola with the given circle.

By the time of Pappus of Alexandria, Greek mathematicians had categorized geometric solutions into three types: ruler-and-compass constructions, constructions using conic sections, and neusis constructions involving a marked ruler, preferring the earlier categories of solution over the later ones. Ibn al-Haytham's solution is of the second type, using hyperbola, through which he develops a neusis constriction. In his 1881 survey of the problem, Marcus Baker calls al-Haytham's solution "excessively prolix and intricate", and quotes Isaac Barrow as expressing a similar opinion. Later in the 11th century, Yusuf al-Mu'taman ibn Hud, a king of the Taifa of Zaragoza in Spain, simplified al-Haytham's lemmas somewhat, but did not make a significant advance on the problem. The work of al-Haytham became known in the rest of Europe through manuscript Latin translations in the 12th or 13th century, and a translation was published in Basel in 1572. Later geometric solutions by Christiaan Huygens, René-François de Sluse, and Guillaume de l'Hôpital used the same idea of an auxiliary conic section: a hyperbola for Huygens, a parabola for Sluse, and both methods for l'Hôpital. Baker cites Huygens's solution as "the most elegant the problem has ever received".

In al-Haytham's solution, the hyperbola is used within a construction of the angle of reflection, after which the point of reflection is easy to find. Instead, Huygens finds a hyperbola that directly solves the problem: the reflection point is a point of intersection between this hyperbola and the given circle. This hyperbola can be characterized in many ways; one way involves inversive geometry. Inverting a point through a circle produces another point, on the same ray from the center of the circle, such that the product of distances of the point and its inverse from the center equals the squared radius of the circle. The locus of points $L$ at which the two lines to the given points cross, at equal angles, a circle concentric to the given one, is a cubic curve containing both given points. The inversion of $L$ through the given circle is a rectangular hyperbola, passing through the two points inverse to the given points and centered at the midpoint of the two inverse points. Its asymptotic lines are parallel to and perpendicular to the angle bisector of the angle subtended by the given points (or their inverses) at the center of the circle. The intersections of this hyperbola with the given circle include the desired solution point or points.

The impossibility of a ruler-and-compass solution was finally proven in 1965, using algebraic methods, by Jack M. Elkin (an actuary). A similar impossibility proof was rediscovered in 1997 by Oxford mathematician Peter M. Neumann. The neusis construction can also be carried out using origami folds following the Huzita–Hatori axioms, and Roger C. Alperin has argued through algebraic methods that the problem can be solved by ruler, compass, and angle trisector, but without providing an explicit construction.

Mechanical

Roberto Marcolongo's reconstruction of a mechanical solution by Leonardo da Vinci. The circle center is pinned to point O, while pins through the given points A and B slide along the caliper arms.The solution is obtained by sliding D onto the given circle.

According to Roberto Marcolongo, a mechanical solution was presented by Leonardo da Vinci, after failing to find a mathematical solution. The solution, as reconstructed by Marcolongo, takes the form of a mechanical linkage that, when placed with its tip pinned to the circle center and the two given points allowed to slide along its arms, always maintains equal angles to these points at the hinge point of the two arms. Therefore, if the mechanism is moved in order to place this hinge point on the given circle, the solution will be obtained at this point.

Algebraic

Later mathematicians such as James Gregory and many others attempted to find an algebraic solution to the problem, using various methods, including analytic methods of geometry and derivation by complex numbers. An algebraic solution to the problem was finally found in 1965 by Elkin, by means of a quartic polynomial. Other solutions were rediscovered later: in 1989, by Harald Riede; in 1990 (submitted in 1988), by Miller and Vegh; and in 1992, by John D. Smith and also by Jörg Waldvogel.

Waldvogel simplifies the algebra by formulating the problem for the unit circle and two given points $a$ and $b$ in the complex plane. With the aid of Huygens's hyperbola Waldvogel derives a quartic equation for the reflection point $\zeta$, $${\bar {a}}{\bar {b}}\zeta ^{4}-({\bar {a}}+{\bar {b}})\zeta ^{3}+(a+b)\zeta ^{2}-ab=0,$$ where ${\bar {a}}$ and ${\bar {b}}$ are the complex conjugates of $a$ and $b$. The roots of this equation might not all lie on the unit circle; the desired solution is the root that does lie on the circle and minimizes the sum of distances to the given points. With some further manipulation this can be reformulated as an equation involving real numbers instead of complex numbers.

Generalization

As well as spherical mirrors, al-Haytham also studied conical and cylindrical mirrors, both of which can be reduced in the same way as a spherical mirror to reflection in a circular mirror in the plane. Researchers have extended Alhazen's problem to general rotationally symmetric quadric mirrors, including hyperbolic, parabolic and elliptical mirrors. They showed that the mirror reflection point can be computed by solving an eighth-degree equation in the most general case. If the camera (eye) is placed on the axis of the mirror, the degree of the equation reduces to six. Alhazen's problem can also be extended to multiple refractions from a spherical ball. Given a light source and a spherical ball of certain refractive index, the closest point on the spherical ball where the light is refracted to the eye of the observer can be obtained by solving a tenth-degree equation.

Another direction for generalization is to non-Euclidean geometry. In the hyperbolic plane, as in the Euclidean plane, it is not possible to solve the problem using only a ruler and compass.

Further reading

• Peña Queralt, Laura; Blanco Abellán, Mónica; Massa Esteve, Maria Rosa (2020), "Mètodes analítics en el s.XVII: l'Hospital i el problema d'Alhazen", Quaderns d'història de l'enginyeria (in Catalan), 18: 13–47, hdl:2117/342686