Jump to content

Discrete dipole approximation codes

Add links
From Wikipedia, the free encyclopedia

Discrete dipole approximation codes. This is a list of Discrete Dipole Approximation (DDA) codes. The "code" here indicates computer code, a particular implementation of the DDA (many of them are open-source). For theoretical approach see Discrete dipole approximation article.

Most of the codes apply to arbitrary-shaped inhomogeneous nonmagnetic particles and particle systems in free space or homogeneous dielectric host medium. The calculated quantities typically include the Mueller matrices, integral cross-sections (extinction, absorption, and scattering), internal fields and angle-resolved scattered fields (phase function). There are some published comparisons of existing DDA codes.[1]

General-purpose open-source DDA codes

[edit]

These codes typically use regular grids (cubical or rectangular cuboid), conjugate gradient method to solve large systems of linear equations, and FFT-acceleration of the matrix-vector products which uses convolution theorem. Complexity of this approach is almost linear in number of dipoles for both time and memory.[2]

Name Authors References Language Updated Features
DDSCAT Draine and Flatau [3] Fortran 2019 (v. 7.3.3) Can also handle periodic particles and efficiently calculate near fields. Uses OpenMP acceleration.
DDscat.C++ Choliy [4] C++ 2017 (v. 7.3.1) Version of DDSCAT translated to C++ with some further improvements.
ADDA Yurkin, Hoekstra, and contributors [5][6] C 2020 (v. 1.4.0) Implements fast and rigorous consideration of a plane substrate, and allows rectangular-cuboid voxels for highly oblate or prolate particles. Can also calculate emission (decay-rate) enhancement of point emitters. Near-fields calculation is not very efficient. Uses Message Passing Interface (MPI) parallelization and can run on GPU (OpenCL).
OpenDDA McDonald [7][8] C 2009 (v. 0.4.1) Uses both OpenMP and MPI parallelization. Focuses on computational efficiency.
DDA-GPU Kieß [9] C++ 2016 Runs on GPU (OpenCL). Algorithms are partly based on ADDA.
VIE-FFT Sha [10] C/C++ 2019 Also calculates near fields and material absorption. Named differently, but the algorithms are very similar to the ones used in the mainstream DDA.
VoxScatter Groth, Polimeridis, and White [11] Matlab 2019 Uses circulant preconditioner for accelerating iterative solvers
IF-DDA Chaumet, Sentenac, and Sentenac [12] Fortran, GUI in C++ with Qt 2021 (v. 0.9.19) Idiot-friendly DDA. Uses OpenMP and HDF5. Has a separate version (IF-DDAM) for multi-layered substrate.
MPDDA Shabaninezhad, Awan, and Ramakrishna [13] Matlab 2021 (v. 1.0) Runs on GPU (using Matlab capabilities)
CPDDA Dibo Xu and others [14] Python 2025 GPU acceleration using CuPy

Specialized DDA codes

[edit]

These list include codes that do not qualify for the previous section. The reasons may include the following: source code is not available, FFT acceleration is absent or reduced, the code focuses on specific applications not allowing easy calculation of standard scattering quantities.


Name Authors References Language Updated Features
DDSURF, DDSUB, DDFILM Schmehl, Nebeker, and Zhang [15][16][17] Fortran 2008 Rigorous handling of semi-infinite substrate and finite films (with arbitrary particle placement), but only 2D FFT acceleration is used.
DDMM Mackowski [18] Fortran 2002 Calculates T-matrix, which can then be used to efficiently calculate orientation-averaged scattering properties.
CDA McMahon [19] Matlab 2006
DDA-SI Loke [20] Matlab 2014 (v. 0.2) Rigorous handling of substrate, but no FFT acceleration is used.
PyDDA Dmitriev Python 2015 Reimplementation of DDA-SI
e-DDA Vaschillo and Bigelow [21] Fortran 2019 (v. 2.0) Simulates electron-energy loss spectroscopy and cathodoluminescence. Built upon DDSCAT 7.1.
DDEELS Geuquet, Guillaume and Henrard [22] Fortran 2013 (v. 2.1) Simulates electron-energy loss spectroscopy and cathodoluminescence. Handles substrate through image approximation, but no FFT acceleration is used.
T-DDA Edalatpour [23] Fortran 2015 Simulates near-field radiative heat transfer. The computational bottleneck is direct matrix inversion (no FFT acceleration is used). Uses OpenMP and MPI parallelization.
CDDA Rosales, Albella, González, Gutiérrez, and Moreno [24] 2021 Applies to chiral systems (solves coupled equations for electric and magnetic fields)
PyDScat Yibin Jiang, Abhishek Sharma and Leroy Cronin [25] Python 2023 Simulates nanostructures undergoing structural transformation with GPU acceleration.
[edit]
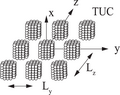
  • Scattering by periodic structures such as slabs, gratings, of periodic cubes placed on a surface, can be solved in the discrete dipole approximation.
    Scattering by periodic structures such as slabs, gratings, of periodic cubes placed on a surface, can be solved in the discrete dipole approximation.
  • Scattering by infinite object (such as cylinder) can be solved in the discrete dipole approximation.
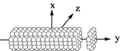
    Scattering by infinite object (such as cylinder) can be solved in the discrete dipole approximation.

See also

[edit]

References

[edit]
  1. ^ Penttilä, Antti; Zubko, Evgenij; Lumme, Kari; Muinonen, Karri; Yurkin, Maxim A.; et al. (2007). "Comparison between discrete dipole implementations and exact techniques" (PDF). J. Quant. Spectrosc. Radiat. Transfer. 106 (1–3). Elsevier BV: 417–436. Bibcode:2007JQSRT.106..417P. doi:10.1016/j.jqsrt.2007.01.026.
  2. ^ M. A. Yurkin; A. G. Hoekstra (2007). "The discrete dipole approximation: an overview and recent developments" (PDF). J. Quant. Spectrosc. Radiat. Transfer. 106 (1–3): 558–589. arXiv:0704.0038. Bibcode:2007JQSRT.106..558Y. doi:10.1016/j.jqsrt.2007.01.034. S2CID 119572857.
  3. ^ Draine, B.T.; P.J. Flatau (1994). "Discrete dipole approximation for scattering calculations". J. Opt. Soc. Am. A. 11 (4): 1491–1499. Bibcode:1994JOSAA..11.1491D. doi:10.1364/JOSAA.11.001491.
  4. ^ V. Y. Choliy (2013). "The discrete dipole approximation code DDscat.C++: features, limitations and plans". Adv. Astron. Space Phys. 3: 66–70. Bibcode:2013AASP....3...66C.
  5. ^ M. A. Yurkin; V. P. Maltsev; A. G. Hoekstra (2007). "The discrete dipole approximation for simulation of light scattering by particles much larger than the wavelength" (PDF). J. Quant. Spectrosc. Radiat. Transfer. 106 (1–3): 546–557. arXiv:0704.0037. Bibcode:2007JQSRT.106..546Y. doi:10.1016/j.jqsrt.2007.01.033. S2CID 119574693.
  6. ^ M. A. Yurkin; A. G. Hoekstra (2011). "The discrete-dipole-approximation code ADDA: capabilities and known limitations" (PDF). J. Quant. Spectrosc. Radiat. Transfer. 112 (13): 2234–2247. Bibcode:2011JQSRT.112.2234Y. doi:10.1016/j.jqsrt.2011.01.031.
  7. ^ J. McDonald; A. Golden; G. Jennings (2009). "OpenDDA: a novel high-performance computational framework for the discrete dipole approximation". Int. J. High Perf. Comp. Appl. 23 (1): 42–61. arXiv:0908.0863. Bibcode:2009arXiv0908.0863M. doi:10.1177/1094342008097914. S2CID 10285783.
  8. ^ J. McDonald (2007). OpenDDA - a novel high-performance computational framework for the discrete dipole approximation (PDF) (PhD). Galway: National University of Ireland.
  9. ^ M. Zimmermann; A. Tausendfreund; S. Patzelt; G. Goch; S. Kieß; M. Z. Shaikh; M. Gregoire; S. Simon (2012). "In-process measuring procedure for sub-100 nm structures". J. Laser Appl. 24 (4): 042010. Bibcode:2012JLasA..24d2010Z. doi:10.2351/1.4719936.
  10. ^ W. E. I. Sha; W. C. H. Choy; Y. P. Chen; W. C. Chew (2011). "Optical design of organic solar cell with hybrid plasmonic system". Opt. Express. 19 (17): 15908–15918. Bibcode:2011OExpr..1915908S. doi:10.1364/OE.19.015908. PMID 21934954.
  11. ^ S. P. Groth; A.G. Polimeridis; J.K. White (2020). "Accelerating the discrete dipole approximation via circulant preconditioning". J. Quant. Spectrosc. Radiat. Transfer. 240 106689. Bibcode:2020JQSRT.24006689G. doi:10.1016/j.jqsrt.2019.106689. S2CID 209969404.
  12. ^ P. C. Chaumet; D. Sentenac; G. Maire; T. Zhang; A. Sentenac (2021). "IFDDA, an easy-to-use code for simulating the field scattered by 3D inhomogeneous objects in a stratified medium: tutorial". J. Opt. Soc. Am. A. 38 (12): 1841–1852. Bibcode:2021JOSAA..38.1841C. doi:10.1364/JOSAA.432685.
  13. ^ M. Shabaninezhad; M. G. Awan; G. Ramakrishna (2021). "MATLAB package for discrete dipole approximation by graphics processing unit: Fast Fourier Transform and Biconjugate Gradient". J. Quant. Spectrosc. Radiat. Transfer. 262 107501. Bibcode:2021JQSRT.26207501S. doi:10.1016/j.jqsrt.2020.107501. S2CID 233839571.
  14. ^ Xu, D.; Tuersun, P.; Li, S.; Wang, M.; Jiang, L. (2025). "CPDDA: A Python Package for Discrete Dipole Approximation Accelerated by CuPy". Nanomaterials. 15 (7): 500. doi:10.3390/nano15070500. PMC 11990789. PMID 40214545.
  15. ^ Schmehl, Roland; Nebeker, Brent M.; Hirleman, E. Dan (1997-11-01). "Discrete-dipole approximation for scattering by features on surfaces by means of a two-dimensional fast Fourier transform technique". J. Opt. Soc. Am. A. 14 (11). The Optical Society: 3026–3036. Bibcode:1997JOSAA..14.3026S. doi:10.1364/josaa.14.003026.
  16. ^ B. M. Nebeker (1998). Modeling of light scattering from features above and below surfaces using the discrete-dipole approximation (PhD). Tempe, AZ, USA: Arizona State University.
  17. ^ E. Bae; H. Zhang; E. D. Hirleman (2008). "Application of the discrete dipole approximation for dipoles embedded in film". J. Opt. Soc. Am. A. 25 (7): 1728–1736. Bibcode:2008JOSAA..25.1728B. doi:10.1364/JOSAA.25.001728. PMID 18594631.
  18. ^ D. W. Mackowski (2002). "Discrete dipole moment method for calculation of the T matrix for nonspherical particles". J. Opt. Soc. Am. A. 19 (5): 881–893. Bibcode:2002JOSAA..19..881M. doi:10.1364/JOSAA.19.000881. PMID 11999964.
  19. ^ M. D. McMahon (2006). Effects of geometrical order on the linear and nonlinear optical properties of metal nanoparticles (PDF) (PhD). Nashville, TN, USA: Vanderbilt University.
  20. ^ V. L. Y. Loke; P. M. Mengüç; Timo A. Nieminen (2011). "Discrete dipole approximation with surface interaction: Computational toolbox for MATLAB". J. Quant. Spectrosc. Radiat. Transfer. 112 (11): 1711–1725. Bibcode:2011JQSRT.112.1711L. doi:10.1016/j.jqsrt.2011.03.012.
  21. ^ N. W. Bigelow; A. Vaschillo; V. Iberi; J. P. Camden; D. J. Masiello (2012). "Characterization of the electron- and photon-driven plasmonic excitations of metal nanorods". ACS Nano. 6 (8): 7497–7504. doi:10.1021/nn302980u. PMID 22849410.
  22. ^ N. Geuquet; L. Henrard (2010). "EELS and optical response of a noble metal nanoparticle in the frame of a discrete dipole approximation". Ultramicroscopy. 110 (8): 1075–1080. doi:10.1016/j.ultramic.2010.01.013.
  23. ^ S. Edalatpour; M. Čuma; T. Trueax; R. Backman; M. Francoeur (2015). "Convergence analysis of the thermal discrete dipole approximation". Phys. Rev. E. 91 (6): 063307. arXiv:1502.02186. Bibcode:2015PhRvE..91f3307E. doi:10.1103/PhysRevE.91.063307. PMID 26172822. S2CID 21556373.
  24. ^ S. A. Rosales; P. Albella; F. González; Y. Gutierrez; F. Moreno (2021). "CDDA: extension and analysis of the discrete dipole approximation for chiral systems". Opt. Express. 29 (19): 30020–30034. Bibcode:2021OExpr..2930020R. doi:10.1364/OE.434061. hdl:10902/24774. PMID 34614734.
  25. ^ Jiang, Yibin; Sharma, Abhishek; Cronin, Leroy (2023). "An Accelerated Method for Investigating Spectral Properties of Dynamically Evolving Nanostructures". The Journal of Physical Chemistry Letters. 14 (16): 3929–3938. doi:10.1021/acs.jpclett.3c00395. PMC 10150391. PMID 37078273.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Discrete_dipole_approximation_codes&oldid=1302400182"