Templat:Infobox mathematical function
Tampilan
| Templat ini menggunakan Lua: |
| name | |
|---|---|
| [[File:{{{image}}}|frameless]] | |
| Domain dan Citra | |
| Domain dari fungsi | domain |
| Sifat umum | |
| Paritas fungsi | parity |
| Periode | period |
| Nilai-nilai spesifik | |
| Nilai di 0 | zero |
| Nilai di | plusinf |
| Nilai di | minusinf |
| Nilai maksimum | max |
| Nilai minimum | min |
| Nilai di vr1 | f1 |
| Nilai di vr2 | f2 |
| Nilai di [...] | [...] |
| Nilai di vr5 | f5 |
| Sifat khusus | |
| Asimtot | asymptote |
| Akar | root |
| Titik kritis | critical |
| Titik belok | inflection |
| Titik tetap | fixed |
notes | |
Sintaks infobox
[sunting sumber]Sintaks sederhana
[sunting sumber]{{Infobox mathematical function
| name=
| image= |imagesize= <!--(default 220px)--> |imagealt=
| parity= |domain= |codomain= |period=
| zero= |plusinf= |minusinf= |max= |min=
| vr1= |f1= |vr2= |f2= |vr3= |f3= |vr4= |f4= |vr5= |f5=
| asymptote= |root= |critical= |inflection= |fixed=
| notes=
}}
Sintaks sepenuhnya
[sunting sumber]{{Infobox mathematical function
| name=
| image= |imagesize= |imagealt= |caption=
| general_definition= |deriver = |motivation_of_creation= |date= |extends= |main_applications= |fields_of_application=
| domain= |codomain= |range =
| parity= |period= |analytic= |meromorphic= |holomorphic=
| zero= |plusinf= |minusinf= |max= |min=
| vr1= |f1= |vr2= |f2= |vr3= |f3= |vr4= |f4= |vr5= |f5=
| asymptote= |root= |critical= |inflection= |fixed= |poles=
| reciprocal= |inverse= |derivative= |antiderivative= |other_related=
| taylor_series= |generalized_continued_fraction= |corresponding_transform= |corresponding_transform_formula=
| notes=
}}
Penjelasan
[sunting sumber]- Parameter
namemengatur nama fungsi yang tertulis di infobox. Gunakan parameter ini jika Anda ingin menulis nama fungsi yang berbeda dari judul artikel (misal karena ingin mengikutkan kode LaTeX. - Parameter
imagedigunakan untuk menambahkan gambar ke infobox. Gunakan imagesize jika Anda ingin mengatur ukuran gambar secara spesifik. Parameterimagealtakan menampilkan informasi tambahan (yang Anda tulis) ketika kursor di-hover ke atas gambar, sedangkancaptionakan menampilkan informasi tersebut di bagian bawah gambar. - Parameter-parameter selanjutnya berisi informasi umum dari fungsi.
general_definitionderivermotivation_of_creationdateextendsmain_applicationsfields_of_application
- Parameter berikutnya berisi tentang himpunan yang terlibat:
domainadalah daerah domain fungsi, sedangkancodomainadalah kodomain fungsi, danrangeadalah citra dari fungsi. - Parameter lain yang Anda dapat sertakan adalah sifat-sifat fungsi secara umum seperti: paritas fungsi (fungsi ganjil atau fungsi genap) pada parameter
parity, dan periode fungsi (jika fungsi tersebut periodik) pada parameterperiod. Parameteranalytic,meromorphic, danholomorphicdisertakan untuk mendeskripsikan jenis fungsi. - Ada beberapa parameter untuk menampilkan informasi tentang nilai-nilai penting fungsi,
zerodiisi dengan nilai fungsi saat . Dengan kata lain, nilai fungsi saat memotong sumbu-yplusinfdanminusinfdiisi dengan nilai fungsi di dan .maxdanminmenandakan nilai maksimum dan nilai minimum dari fungsi- Pasangan parameter
vr1danf1,vr2danf2, dan seterusnya, digunakan untuk menyajikan nilai spesifik dari fungsi. Sebagai contoh, misalkan sebuah fungsi di titik memiliki nilai , dan hal ini adalah suatu hal yang penting, atau akibat dari sesuatu yang spesifik. Dalam kasus ini, Anda sebaiknya menambahkan|vr1= |f1=. Saat ini infobox hanya dapat menyertakan lima titik; diskusikan di halaman pembicaraan jika Anda membutuhkan parameter yang lebih banyak.
- Juga ada parameter yang menampilkan titik penting dari fungsi
asymptoteberisi titik asimtot dari fungsirootberisi akar-akar dari fungsi; yakni titik-titik yang menyebabkan nilai fungsi sama dengan nolcritical,inflection,fixed, secara berurutan menandakan titik kritis, titik infleksi, dan titik tetap dari fungsipolesberisi titik titik kutub dari fungsi.
- Parameter
taylor_seriesdangeneralized_continued_fractiondigunakan untuk menyertakan definisi deret dari fungsi corresponding_transformdancorresponding_transform_formula
Contoh
[sunting sumber]Kode berikut akan menampilkan kotak infobox disamping
| Sine | |
|---|---|
 | |
| Informasi umum | |
| Definisi umum | |
| Tujuan diciptakan | Indian astronomy |
| Tanggal penemuan solusi | Gupta period |
| Bidang penerapan | Trigonometry, Integral transform, etc. |
| Domain dan Citra | |
| Domain dari fungsi | (−∞, +∞) a |
| Sifat umum | |
| Paritas fungsi | odd |
| Periode | 2π |
| Nilai-nilai spesifik | |
| Nilai di 0 | 0 |
| Nilai maksimum | (2kπ + π2, 1)b |
| Nilai minimum | (2kπ − π2, −1) |
| Sifat khusus | |
| Akar | kπ |
| Titik kritis | kπ + π2 |
| Titik belok | kπ |
| Titik tetap | 0 |
| Kebalikan | Cosecant |
| Invers | Arcsine |
| Turunan | |
| Antiturunan | |
| Fungsi yang relevan | cos, tan, csc, sec, cot |
| Definisi deret | |
| Deret Taylor | |
| Pecahan berlanjut | |
| Gamma | |
|---|---|
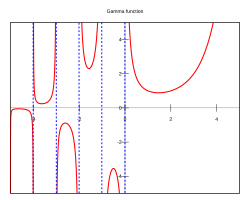 The gamma function along part of the real axis | |
| Informasi umum | |
| Definisi umum | , |
| Pencipta | Daniel Bernoulli |
| Tujuan diciptakan | Interpolation for factorial function |
| Tanggal penemuan solusi | 1720s |
| Perumuman dari | Factorial function |
| Digunakan di | probability-distribution functions |
| Bidang penerapan | Probability, statistics, combinatorics |
| Domain dan Citra | |
| Domain dari fungsi | - ℤ0- |
| Sifat umum | |
| Paritas fungsi | Not even and not odd |
| Periode | No |
| Analitik? | Yes |
| Meromorfik? | Yes |
| Holomorfik? | Yes except at ℤ0- |
| Nilai-nilai spesifik | |
| Nilai maksimum | No |
| Nilai minimum | No |
| Nilai di ℤ+ | |
| Nilai di ℤ0- | Not defined |
| Sifat khusus | |
| Akar | No |
| Titik kritis | ℤ0- |
| Titik belok | ℤ0- |
| Titik tetap | 1 |
| Transformasi | |
| Transformasi yang berkaitan | Mellin transform |
| Formula transformasi | |
{{Infobox mathematical function
| name = Sine
| image = Sine one period.svg
|general_definition = <math>\sin(\alpha) = \frac {\textrm{opposite}} {\textrm{hypotenuse}}</math>
| parity=odd
|domain=(−{{lower|0.2em|{{resize|130%|∞}}}}, +{{lower|0.2em|{{resize|130%|∞}}}}) {{smallsup|a}}
|codomain=[−1, 1] {{smallsup|a}} |period=2{{pi}}
| zero=0 |plusinf= |minusinf=
|max=(2''k''{{pi}} + {{sfrac|{{pi}}|2}}, 1){{smallsup|b}} |min=(2''k''{{pi}} − {{sfrac|{{pi}}|2}}, −1)
| vr1= |f1= <!--......--> |vr5= |f5=
| asymptote= |root=''k''{{pi}}
|critical=''k''{{pi}} + {{sfrac|{{pi}}|2}}
|inflection=''k''{{pi}}
|fixed=0
| notes = {{ublist |{{sup|a}} For [[Real number|real]] numbers. |{{sup|b}} Variable ''k'' is an [[integer]].}}
|fields_of_application= [[Trigonometry]], [[Integral transform]], etc.
|date=[[Gupta period]]
|motivation_of_creation=[[Indian astronomy]]
|reciprocal = [[Cosecant]]
|inverse = [[Arcsine]]
|derivative = <math>f'(x) = \cos(x) </math>
|antiderivative = <math>\int f(x)\,dx = -\cos(x) + C </math>
|generalized_continued_fraction = <math>
\cfrac{x}{1 + \cfrac{x^2}{2\cdot3-x^2 +
\cfrac{2\cdot3 x^2}{4\cdot5-x^2 +
\cfrac{4\cdot5 x^2}{6\cdot7-x^2 + \ddots}}}}.
</math>
|taylor_series= <math>
\begin{align}
x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \\[8pt]
& = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{2n+1} \\[8pt]
\end{align}
</math>
|other_related= cos, tan, csc, sec, cot
}}









![{\displaystyle {\begin{aligned}x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\\[8pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91b7e722b0e78f16453f0b08592125448c3a0d8e)






