Variogramm
Ein Variogramm (von altgriechisch γραφειν graphēin (be-)schreiben und lateinisch variabilis veränderlich) bezeichnet in der Geostatistik eine grafische Darstellung der räumlichen Abhängigkeit (Autokorrelation) zwischen Datenpunkten.[1] Häufig wird synonym auch der Begriff Semivariogramm (vom lateinischen Präfix semi- für etwas halbes) verwendet, der aber gelegentlich auch nur das halbe Variogramm bezeichnet und daher vermieden werden sollte.[2] Genauso kann die Bezeichnung Semivarianz irreführend sein, da die im Variogramm dargestellten Werte die gesamte Varianz von Beobachtungen eines bestimmten räumlichen Abstands (Lag) wiedergeben.[2]

Das Variogramm ist von zentraler Funktion in der Geostatistik, da es zur Anpassung eines Modells der zeitlichen bzw. räumlichen Korrelation des beobachteten Phänomens verwendet wird. Man unterscheidet daher zwischen dem experimentellen Variogramm, das eine mögliche räumliche bzw. zeitliche Korrelation visualisiert, und dem Variogramm-Modell, das anschließend zur Bestimmung der Gewichte der Kriging-Funktion genutzt wird. Das experimentelle Variogramm ist eine empirische Schätzung der Kovarianz eines gaußschen Prozesses und ist daher möglicherweise nicht positiv definit, wodurch es ohne Einschränkungen oder zusätzliche Verarbeitung nicht direkt für Kriging einsetzbar ist. Daher ist auch nur eine begrenzte Zahl von Variogramm-Modellen populär, hauptsächlich häufigsten das lineare, sphärische, gaußsche und exponentielle Modell.
Aufbau
[Bearbeiten | Quelltext bearbeiten]Ein Variogramm beschreibt die Unterschiede zwischen einer Variablen („Messwerten“), die an verschiedenen Punkten in einem Raum gemessen wurde. Dabei gehen die räumlichen Abstände zwischen den Messpunkten und die Unterschiede zwischen den Messwerten ein, sodass die Varianz (Streuung) der Messwerte in Abhängigkeit von der Entfernung der Messpunkte darstellbar wird (Regionalisierung). Diese Beziehung ist beim Interpolieren etwa beim Kriging von großer Bedeutung. Für die Schätzung eines empirischen Variogramms anhand einer Stichprobe werden zunächst die Abstände zwischen den Messpunkten für alle möglichen Paarbildungen der Messpunkte ermittelt.[3] Im nächsten Schritt werden Entfernungsklassen (engl. lags) definiert, und jedes Punktpaar wird entsprechend dem Abstand zwischen den beiden Punkten einer der Klassen zugewiesen. Nun wird der Unterschied – die Differenz – zwischen den beiden Messwerten des Paares ermittelt und quadriert. Schließlich werden alle diese quadrierten Differenzen summiert und durch die Anzahl der Punktpaare in dieser Entfernungsklasse geteilt. Dieser Wert wird halbiert, weil bei der Differenz ja jeweils zwei Messwerte beteiligt sind. Wegen der Halbierung wird dem Begriff das Präfix semi- vorangesetzt. Das Ergebnis ist ein Schätzwert der Semivarianz für die untersuchte Entfernungsklasse. Die für alle Klassen ermittelten Semivarianzen werden in einem zweidimensionalen Diagramm als Punkte eingetragen: auf der Abszisse die Entfernungsklassen, und auf der Ordinate die zur Klasse gehörige Semivarianz.
Die empirische Semivarianz einer Stichprobe ist von mathematischen Modellen der Semivarianz (theoretische Variogrammfunktion) zu unterscheiden, welche die Abhängigkeit der Semivarianz von den Messpunktabständen als stetige Funktion mit einer mathematischen Formel modellieren. Diese stetige Funktion ergibt für jeden Abstandswert einen Funktionswert, während die empirische Semivarianz als Punktschätzung stets die Information einer Entfernungsklasse zusammenfasst und daher für die gesamte Klasse gilt.
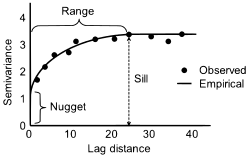
Häufig werden in einem Variogramm sowohl die empirische Semivarianz als auch ein theoretisches Variogrammmodell zusammen abgetragen. I. d. R. wird dann das theoretische Modell als stetiger Funktionsgraph in Form einer (gekurvten) Linie gezeichnet und die Semivarianzwerte der Klassen werden als schwarze Punkte eingetragen.
Zu den gebräuchlichsten theoretischen Modellen zählen:
- sphärisches
- exponentielles
- lineares
- gaußsches Variogramm.
Zur Beschreibung des Verlaufes eines Variogrammes werden v. a. drei Begriffe verwendet, Schwelle, Reichweite und Nugget-Effekt. Weist die untersuchte räumliche Variable (der Messwert) eine in ihrer Reichweite begrenzte räumliche Autokorrelation auf, so ergeben sich bei Entfernungsklassen, welche diese Reichweite überschreiten, nur noch zufällige, also nicht mehr strukturbedingte Schwankungen der Semivarianz. Ein theoretisches Variogrammmodell (Ausnahmen: lineares Variogramm) verläuft dann gegen einen Grenzwert (engl. sill, wörtlich Schwelle). Die Entfernungsklasse bzw. der Entfernungswert zwischen Punktpaaren, an dem die Schwelle erreicht wird, entspricht der Reichweite (engl. range) der Autokorrelation. Bei räumlichen Phänomenen können manchmal selbst bei sehr kleinen Abständen noch deutliche Messwertunterschiede auftreten. So trifft man etwa bei der Beprobung einer Goldseife aufgrund der Kornsortierung in der Seife manchmal direkt nebeneinander taubes Gestein und Goldnuggets an. In Anlehnung daran wird der Semivarianzwert bei einem gegen Null gehenden Abstand zwischen Messpunkten auch Nugget-Effekt genannt. Der Nugget-Effekt bezeichnet beim theoretischen Variogrammmodell also den Funktionswert, den der theoretische Graph bei Abstand Null annimmt. Dieser Wert kann als ein Maß für das statistische Rauschen verstanden werden.
Verwendung
[Bearbeiten | Quelltext bearbeiten]Variogramm-basierte Scoring rules können für verbesserte multivariate Vorhersagen genutzt werden, bei denen die Korrelationsstruktur explizit betrachtet wird[4].
Standardliteratur
[Bearbeiten | Quelltext bearbeiten]- R. Webster, M. Oliver: Geostatistics for environmental scientists. Wiley, Chichester 2007 (2. Aufl.).
- H. Wackernagel: Multivariate Geostatistics. Springer, Berlin / Heidelberg / New York 1995.
- J. P. Chiles, P. Delfiner: Geostatistics: Modelling Spatial Uncertainty. Wiley, New York 1999.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Variogramm auf Geographic Information Technology Training Alliance
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Variogramm. In: Lexikon der Geographie. Spektrum, abgerufen am 19. November 2025.
- ↑ a b Martin Bachmaier, Matthias Backes: Variogram or Semivariogram? Variance or Semivariance? Allan Variance or Introducing a New Term? In: Mathematical Geosciences. Band 43, Nr. 6, August 2011, ISSN 1874-8961, S. 735–740, doi:10.1007/s11004-011-9348-3 (springer.com [abgerufen am 19. November 2025]).
- ↑ Richard Webster, Margaret Oliver: Geostatistics for environmental scientists (= Stephen Senn, Marion Scott [Hrsg.]: Statistics in Practice). 2. Auflage. Wiley, Chichester 2007, ISBN 978-0-470-02858-2, 4.9 Estimating Semivariances and Covariances, S. 67–68, (4.40) (englisch).
- ↑ Variogram-Based Proper Scoring Rules for Probabilistic Forecasts of Multivariate Quantities Michael Scheuerer, Thomas M. Hamill, Print Publication: 01 Apr 2015, DOI: https://doi.org/10.1175/MWR-D-14-00269.1, https://journals.ametsoc.org/view/journals/mwre/143/4/mwr-d-14-00269.1.xml
