প্রবেশদ্বার:গণিত

রাফায়েলের কল্পনায় ৩য় শতাব্দীর বিখ্যাত গণিতবিদ ইউক্লিড, দ্য স্কুল অফ এথেন্স ছবির অংশবিশেষ।

গণিত হল জ্ঞানের একটি ক্ষেত্র যাতে সংখ্যা, সূত্র এবং সম্পর্কিত কাঠামো, আকার এবং সেগুলির মধ্যে থাকা স্থানগুলি এবং পরিমাণ এবং তাদের পরিবর্তনগুলি অন্তর্ভুক্ত থাকে। এই বিষয়গুলি যথাক্রমে সংখ্যা তত্ত্বের প্রধান উপশাখা, বীজগণিত,  জ্যামিতি, এবং বিশ্লেষণ। তবে একাডেমিক শৃঙ্খলার জন্য একটি সাধারণ সংজ্ঞা সম্পর্কে গণিতবিদদের মধ্যে কোন সাধারণ ঐকমত্য নেই।

গণিতে সংখ্যা ও অন্যান্য পরিমাপযোগ্য রাশিসমূহের মধ্যকার সম্পর্ক বর্ণনা করা হয়। গণিতবিদগন বিশৃঙ্খল ও অসমাধানযুক্ত সমস্যাকে শৃঙ্খলভাবে উপস্থাপনের প্রক্রিয়া খুঁজে বেড়ান ও তা সমাধানে নতুন ধারণা প্রদান করে থাকেন। গাণিতিক প্রমাণের মাধ্যমে এই ধারণাগুলির সত্যতা যাচাই করা হয়। গাণিতিক সমস্যা সমাধান সম্পর্কিত গবেষণায় বছরের পর বছর, যুগের পর যুগ বা শত শত বছর পর্যন্ত লেগে যেতে পারে। গণিতের সার্বজনীন ভাষা ব্যবহার করে বিজ্ঞানীরা একে অপরের সাথে ধারণার আদান-প্রদান করেন। গণিত তাই বিজ্ঞানের ভাষা।

১৭শ শতক পর্যন্ত কেবল পাটিগণিত, বীজগণিত ও জ্যামিতিকে গাণিতিক শাস্ত্র হিসেবে গণ্য করা হত। সেসময় গণিত দর্শন ও বিজ্ঞানের চেয়ে কোন পৃথক শাস্ত্র ছিল না। আধুনিক যুগে এসে গণিত বলতে যা বোঝায়, তার গোড়াপত্তন করেন প্রাচীন গ্রিকেরা, পরে মুসলমান পণ্ডিতেরা এগুলি সংরক্ষণ করেন, অনেক গবেষণা করেন এবং খ্রিস্টান পুরোহিতেরা মধ্যযুগে এগুলি ধরে রাখেন। তবে এর সমান্তরালে ভারতে এবং চীন-জাপানেও প্রাচীন যুগ ও মধ্যযুগে স্বতন্ত্রভাবে উচ্চমানের গণিতচর্চা করা হত। ভারতীয় গণিত প্রাথমিক ইসলামী গণিতের উপর গভীর প্রভাব ফেলেছিল। ১৭শ শতকে এসে আইজাক নিউটন ও গটফ্রিড লাইবনিৎসের ক্যালকুলাস উদ্ভাবন এবং ১৮শ শতকে অগুস্তঁ লুই কোশি ও তার সমসাময়িক গণিতবিদদের উদ্ভাবিত কঠোর গাণিতিক বিশ্লেষণ পদ্ধতিগুলির উদ্ভাবন গণিতকে একটি একক, স্বকীয় শাস্ত্রে পরিণত করে। তবে ১৯শ শতক পর্যন্ত কেবল পদার্থবিজ্ঞানী, রসায়নবিদ ও প্রকৌশলীরাই গণিত ব্যবহার করতেন। (সম্পূর্ণ নিবন্ধ...)

• 

  

  কালো রেখাটি একটি ফাংশন ও লাল রেখাটি এর একটি স্পর্শক নির্দেশ করছে। স্পর্শক রেখাটির ঢাল চিত্রে দেখানো বিন্দুতে ফাংশনটির অন্তরজের সমান হবে।

  
  কোন ফাংশনের অন্তরকলজ বা অন্তরক সহগ বা ডেরিভেটিভ স্বাধীন চলকের সূক্ষ্মাতিসূক্ষ্ম পরিবর্তনের জন্য ফাংশনের (অধীন চলকের) পরিবর্তন নির্ণয় করে। অন্তরজ ক্যালকুলাসের মৌলিক অংশ। উদাহরনস্বরূপ, কোন বস্তুর বেগ হল সময়ের সাপেক্ষে তার অবস্থান পরিবর্তনের অন্তরজ বা হার। এটি নির্দেশ করে বস্তুটি সময়ের সাথে কীভাবে অবস্থান পরিবর্তন করছে। একটিমাত্র চলকের জন্য কোন ফাংশনের কোন একটি বিন্দুতে যখন অন্তরজের মান থাকে তখন তা ফানশনের সেই বিন্দুতে স্পর্শকের ঢালের মানের সমান হয়। স্পর্শক রেখাটি গৃহীত মানের কাছাকাছি ফাংশনটির সর্বোচ্চ রৈখিক অণুমান। তাই অন্তরজকে প্রায়ই তাৎক্ষনিক পরিবর্তনের হার হিসবে বর্ণনা করা হয়। অন্যভাবে, অধীন চলকের তাৎক্ষনিক পরিবর্তন, স্বাধীন চলকের পরিবর্তনের অণুপাত।
  
  অন্তরজকে বিভিন্ন বাস্তব চলকের ফাংশনে প্রয়োগ করা যেতে পারে। এই সিদ্ধান্তে, অন্তরজকে রৈখিক রূপান্তর হিসেবে প্রকাশ করা যেতে পারে যার যার লেখচিত্র (রুপান্তরের পর) আসল লেখচিত্রের সর্বোচ্চ রৈখিক অণুমান। জ্যাকবিয়ান ম্যাট্রিক্স হল এমন ম্যাট্রিক্স যা নির্ধারিত স্বাধীন ও নির্ভরশীল চলকের ভিত্তিতে এই রৈখিক রূপান্তর প্রকাশ করে। স্বাধীন চলকের সাপেক্ষে এটা আংশিক অন্তরজ নির্ণয় করতে পারে। বিভিন্ন চলকের বাস্তব-মানের-ফাংশনের জন্য জ্যাকবিয়ান ম্যাট্রিক্স গ্র্যাডিয়েন্ট ভেক্টরের ব্যবহার হ্রাস করে। কোন ফাংশনের অন্তরজ নির্ণেয়ের প্রক্রিয়াকে অন্তরীকরণ বা ব্যাবকলন বলে। এর বিপরীত প্রক্রিয়াকে বলে প্রতি-অন্তরজ। ক্যাকুলাসের মৌলিক তত্ত্ব বলে যে, প্রতি-অন্তরজ ও সমাকলন একই কথা। অন্তরীকরণ ও সমাকলন এক চলকীয় ক্যালকুলাসে দুটি মৌলিক প্রক্রিয়া স্থাপন করেছে। (সম্পূর্ণ নিবন্ধ...)
• 

  

  ২ভিত্তিক লগারিদমের লেখচিত্র x অক্ষের (আনুভূমিক অক্ষ) ১ বিন্দুতে ছেদ করে এবং (২, ১), (৪, ২), এবং (৮, ৩) বিন্দু দিয়ে অতিক্রম করে।. উদাহরণস্বরূপ, {{{1}}}, কারণ {{{1}}} রেখাটি ক্রমশ y অক্ষের নিকটবর্তী হতে থাকে কিন্তু কখনও yঅক্ষের সাথে মিলিত হয় না বা ছেদ করে না।.

  
  
  গণিতশাস্ত্রে লগারিদম বা লঘুগণিত হলো সূচকের বিপরীত প্রক্রিয়া। এর অর্থ কোনো সংখ্যার লগারিদম হলো সেই সূচক যেটাকে একটি নির্ধারিত মানের (ভিত্তি) ঘাত হিসাবে উন্নীত করলে প্রথমোক্ত সংখ্যাটি পাওয়া যায়। সহজভাবে, একটি সংখ্যাকে বার বার গুণ করলে, লগারিদম সংখ্যাটিকে যতবার গুণ করা হয়েছিল তা গণনা করে। যেমন: যেহেতু 1000 = 10 × 10 × 10 = 10³ তাই 1000 এর দশ ভিত্তিক লগারিদম হলো 3, অথবা log₁₀ (1000) = 3। x এর b ভিত্তিক লগারিদম কে লেখা হয় log_bx
  
  10 ভিত্তিবিশিষ্ট লগকে (অর্থাৎ b=10) সাধারণ লগারিদম বলা হয় এবং এটিকে বিজ্ঞানী ও প্রকৌশলীরা সাধারণত ব্যবহার করে থাকে। স্বাভাবিক লগারিদমে ভিত্তি হিসেবে গাণিতিক ধ্রুবক e(অর্থাৎ b≈2.718) কে ব্যবহার করা হয়। গণিতবিদ ও পদার্থবিদ গণ স্বাভাবিক লগারিদম ব্যবহার করে থাকে। বাইনারি লগে 2 কে ভিত্তি হিসেবে ব্যবহার করা হয় এবং কম্পিউটার বিজ্ঞানে ব্যবহৃত হয়। (সম্পূর্ণ নিবন্ধ...)
• 

  

  এই ওজন স্কেলের ওজনকারী কড়াই শূন্য বস্তু ধারণ করেছে যা দুটি সমান ভাগে বিভক্ত হয়েছে ।

  
  
  শূন্য একটি জোড় সংখ্যা। কোন পূর্ণসংখ্যা জোড় হওয়া বলতে কী বোঝায়, তা ব্যাখ্যা করার বেশ কিছু উপায় আছে এবং শূন্য সংখ্যাটি এরকম সমস্ত সংজ্ঞাই সিদ্ধ করে: শুন্য ২ এর গুণিতক, ২ দিয়ে বিভাজ্য এবং নিজের সাথে একটি পূর্ণসংখ্যার যোগফলের সমান। এই সংজ্ঞাগুলি কেবল শূন্যের জন্যই ব্যতিক্রমীভাবে প্রযোজ্য নয়, বরং এগুলি জোড় সংখ্যার যোগফল ও গুণফলের সাধারণ নিয়ম দ্বারা ব্যাখ্যা করা যায়।
  
  জোড় সংখ্যাগুলির মধ্যে শূন্য কেন্দ্রীয় ভূমিকা পালন করে। শূন্য জোড় পূর্ণসংখ্যার পরিচয়সূচক উপাদান, এবং এটি পর্যায়ক্রমে আসা সকল উপাদানের ভিত্তি কেস। শূন্যের জোড় হবার প্রবণতার সরাসরি প্রয়োগের প্রমাণ আছে এবং এর কাঠামো জোড় সংখ্যার অনুরুপ। সাধারণভাবে, ০ সকল পূর্ণ সংখ্যা দ্বারা বিভাজ্য, যার মধ্যে দুই এর সকল ঘাত আছে। ফলে শূন্য সকল সংখ্যার মধ্যে সবচেয়ে বেশি জোড়। (সম্পূর্ণ নিবন্ধ...)
• 

  

  রাফায়েলের আঁকা স্কুল অব দি অ্যাথেন্স– যেখানে একজন গ্রিক গণিতবিদকে মুখ্যরূপে চিত্রায়ন করা হয়েছে। এতে খুব সম্ভবত ইউক্লিড অথবা আর্কিমিডিসকে কম্পাস দিয়ে একটি জ্যামিতিক চিত্র অঙ্কনরত অবস্থায় উপস্থাপন করা হয়েছে।

  
  
  আলেকজান্দ্রিয়ার গ্রিক গণিতবিদ ইউক্লিড জ্যামিতির উপর লেখা তার "এলিমেন্টস" গ্রন্থে যে ধরনের গাণিতিক পদ্ধতির আলোচনা করেছেন সেটাই এখন ইউক্লিডীয় জ্যামিতি নামে পরিচিত। ইউক্লিডীয় পদ্ধতি সজ্ঞাতভাবে আবশ্যিক স্বতঃসিদ্ধসমূহের একটি ক্ষুদ্র সেটের অনুমান এবং এসব অনুমান থেকে প্রাপ্ত অন্যান্য অনেক প্রতিজ্ঞা র মত (উপপাদ্য) সিদ্ধান্তের অন্তর্ভুক্ত। যদিও ইউক্লিডের প্রাপ্ত অনেক ফলাফলই তার পূর্বতন গণিতবিদেরা আলোচনা করেছিলেন, তাসত্ত্বেও একটি বিস্তৃত অবরোহী এবং যৌক্তিক পদ্ধতির মধ্যে এসব প্রতিজ্ঞা কীভাবে সন্নিবেশ করা যায় তা ইউক্লিডই প্রথম দেখিয়েছিলেন। সমতল জ্যামিতি নিয়ে যাত্রা শুরু করা এলিমেন্টস গ্রন্থটি স্বতঃসিদ্ধ ব্যবস্থা এবং গাণিতিক প্রমাণের প্রথম উদাহরণ হিসেবে মাধ্যমিক পর্যায়ের পাঠ্যক্রমের অংশরূপে আজও পড়ানো হয়ে থাকে। এটি ত্রিমাত্রিক ক্ষেত্র ব্যবস্থার কঠিন জ্যামিতির সাথে মানানসই। এলিমেন্টসের বেশিরভাগ আলোচনা থেকে যে ফলাফল পাওয়া যায় জ্যামিতিক ভাষায় তা এখন বীজগণিত ও সংখ্যাতত্ত্ব নামে পরিচিত।
  
  বিগত দুই হাজার বছরেরও বেশি সময় যাবৎ অন্য কোন ধরনের জ্যামিতির আবির্ভাব না ঘটায় "ইউক্লিডীয়" (Euclidean) বিশেষণটি এতদিন অপ্রয়োজনীয় ছিল। সমান্তরাল রেখার স্বীকার্যের ব্যতিক্রমের সম্ভাবনা সত্ত্বেও
  ইউক্লিডের অন্যান্য স্বতঃসিদ্ধগুলো সজ্ঞাতভাবে এতটাই অনস্বীকার্য মনে হত যে এগুলোর মাধ্যমে প্রমাণিত যে কোনো উপপাদ্যকে পরমভাবে এমনকি অপার্থিব অর্থেও সত্য বলে গণ্য করা হত। বর্তমান সময়ে স্বতঃসঙ্গত অনেক অ-ইউক্লিডীয় জ্যামিতির দেখা পাওয়া যায় যার প্রথমটি ১৯শ শতকে গোড়ায় আবিষ্কৃত হয়েছে। অ্যালবার্ট আইনস্টাইনের সাধারণ আপেক্ষিকতার তত্ত্বের একটি অন্তর্নিহিত বিষয় হল এই যে, স্বয়ং ভৌত ক্ষেত্র ইউক্লিডীয় নয়। এবং মহাকর্ষীয় ক্ষেত্রের সামর্থ্যের সাপেক্ষে ইউক্লিডীয় স্থান বা ক্ষেত্র কেবল স্বল্প দূরত্বের জন্য ভাল একটি অনুমান। (সম্পূর্ণ নিবন্ধ...)
• 

  

  যৌগিক সংখ্যাগুলিকে আয়তাকারে সাজানো যেতে পারে তবে মৌলিক সংখ্যাগুলিকে সাজানো যায় না।

  
  
  গণিতের পরিভাষায় মৌলিক সংখ্যা (অথবা মৌলিক) হল এমন স্বাভাবিক সংখ্যা যার কেবলমাত্র দুটো পৃথক উৎপাদক আছে: ১ এবং ঐ সংখ্যাটি নিজে। ১ এর চেয়ে বড় যে সকল সংখ্যা মৌলিক না তাদেরকে যৌগিক সংখ্যা বলে। অর্থাৎ যে সংখ্যাকে অন্য কোন সংখ্যা দ্বারা ভাগ করা যায় না, তাকে মৌলিক সংখ্যা বলে।পাটিগণিতের মৌলিক উপপাদ্য এর মাধ্যমে সংখ্যাতত্ত্বে মৌলিকের ভূমিকা প্রবেশ করানো হয়। ১ এর উপরে যেকোনো মৌলিক সংখ্যাকে ১ বাদে তার আগ পর্যন্ত সকল মৌলিক সংখ্যার গুনফল হিসাবে প্রকাশ করা যায়। কোনো সংখ্যার মৌলিকতা নির্ণয়ের সহজ কিন্তু ধীর পদ্ধতি হচ্ছে পরীক্ষামূলক ভাগ, যাতে দেখতে হয় সংখ্যা n, ২ থেকে শুরু করে n এর বর্গমূল পর্যন্ত কোনো দুইটি সংখ্যার গুনফল কিনা। পরীক্ষামূলক ভাগের চেয়ে অনেক বেশি কার্যকরি পদ্ধতি হচ্ছে মিলার-রাবিন মৌলিকতা পরীক্ষা যা দ্রুত কিন্তু সামান্য সম্ভাবনা থাকে ভুলের এবং একেএস মৌলিকতা পরীক্ষা, যেটাতে সবসময়ে সঠিক উত্তর আসে বহুঘাত সময়ে, কিন্তু অনেক ধীর। বিশেষ রুপের মৌলিক সংখ্যার জন্য দ্রুতগতির পদ্ধতি আছে, যেমন মার্সেন সংখ্যাদের জন্য। , সর্ববৃহৎ মৌলিক সংখ্যাতে ২৩২৪৯২৫ টি অঙ্ক আছে। প্রথম ছাব্বিশটি মৌলিক সংখ্যা হল:
  ২, ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯, ২৩, ২৯, ৩১, ৩৭, ৪১, ৪৩, ৪৭, ৫৩, ৫৯, ৬১, ৬৭, ৭১, ৭৩, ৭৯, ৮৩, ৮৯, ৯৭, ১০১। ৩ এর চেয়ে বড় প্রত্যেক মৌলিক সংখ্যার বর্গকে ১২ দ্বারা ভাগ করলে ১ অবশিষ্ট থাকে। (সম্পূর্ণ নিবন্ধ...)
• 

  

  স্বাভাবিক সংখ্যা গণনার কাজে ব্যবহার করা হয়, যেমন ১টি আপেল, ২টি আপেল ইত্যাদি

  
  গণিতে স্বাভাবিক সংখ্যা হলো সেইসব পূর্ণসংখ্যা যা গণনার কাজে (যেমন ৫টি আপেল) বা ক্রম নির্দেশ করতে (যেমন চট্টগ্রাম বাংলাদেশের ২য় বৃহত্তম শহর) ব্যবহার করা হয়। স্বাভাবিক সংখ্যা মানুষের ব্যবহার করা সবচেয়ে আদিম সংখ্যা পদ্ধতিগুলোর একটি। মানুষ প্রতিদিনের গণনার কাজে এই সংখ্যাগুলো ব্যবহার করে। গণনার জন্য ব্যবহৃত সংখ্যাগুলোকে অঙ্কবাচক সংখ্যা এবং ক্রম করার জন্য ব্যবহৃত সংখ্যাগুলিকে ক্রমবাচক সংখ্যা বলা হয়।স্বাভাবিক সংখ্যাগুলি সেট তৈরি করে। স্বাভাবিক সংখ্যার সেটকে ধারাবাহিকভাবে প্রসারিত করে আরও অনেক সংখ্যার সেট তৈরি করা হয়: পূর্ণসংখ্যা,মূলদ সংখ্যা,বাস্তব সংখ্যা; জটিল সংখ্যা,ইত্যাদি।
  
  স্বাভাবিক সংখ্যার সেটে শূন্যকে অন্তর্ভুক্ত করা নিয়ে মতভেদ রয়েছে। কেউ কেউ শুধু ধনাত্মক পূর্ণসংখ্যাকে স্বাভাবিক সংখ্যাকে বলেন {১,২,৩, ...}, কেউ কেউ অঋণাত্মক সংখ্যার সেট {০,১,২,৩, ...} দিয়ে সংজ্ঞা প্রদান করেন। প্রথম সংজ্ঞাটি প্রাচীনকাল থেকে চলে আসছে, দ্বিতীয়টি উনিশ শতকে জনপ্রিয় হয়। (সম্পূর্ণ নিবন্ধ...)
• 

  

  স্যার হেনরি বিলিংসলি অনূদিত মৌলিক উপাদানসমূহ-এর প্রথম ইংরেজি অনুবাদ Elements, ১৫৭০

  
  মৌলিক উপাদানসমূহ (গ্রিক ভাষায়: Στοιχεῖα, ইংরেজি: Elements) হল প্রাচীন গ্রিক গণিতবিদ ইউক্লিড রচিত ১৩ খণ্ডবিশিষ্ট একটি গাণিতিক ও জ্যামিতিক গ্রন্থসমগ্র। এটি আলেকজান্দ্রিয়ায় প্রায় খ্রিস্টপূর্ব ৩০০ সালে রচিত। এতে রয়েছে সংজ্ঞা, স্বতঃসিদ্ধ, সূত্র ও অনুসিদ্ধান্ত এবং বিভিন্ন প্রস্তাবনার গাণিতিক প্রমাণ। এই ১৩টি বইয়ে অন্তর্ভুক্ত রয়েছে ইউক্লিডিয় জ্যামিতি এবং সংখ্যাতত্ত্বের প্রাচীন গ্রিক সংস্করণ। মৌলিক উপাদানসমূহ বর্তমান সময় পর্যন্ত টিকে থাকা গণিতের প্রাচীনতম নিদর্শন, এবং যুক্তিবিদ্যা ও আধুনিক বিজ্ঞানের বিকাশের অন্যতম প্রধান সহায়ক। ইউক্লিডের মৌলিক উপাদানসমূহ বইটি ইতিহাসের সবচেয়ে সফল পাঠ্যপুস্তক। ছাপাখানা আবিষ্কারের পর সর্বপ্রথম মুদ্রিত হওয়া বইগুলোর মধ্যে এটি অন্যতম, এবং ১০০০ এরও বেশি সংখ্যকবার মুদ্রিত হবার জন্য মুদ্রণ সংখ্যার দিক থেকে বাইবেলের পরে দ্বিতীয়। বইটি প্রায়
  ২০০০ বছর ধরে জ্যামিতির শিক্ষায় মূল্য পাঠ্য হিসেবে ব্যবহৃত হয়েছে। বহু শতাব্দী ধরে, যখন বিশ্ববিদ্যালয়ের পাঠ্যসূচীতে কোয়াড্রিভিয়াম অন্তর্ভুক্ত হয়, তখন মৌলিক উপাদানসমূহ-এর অন্তত একটি অংশের পাঠ সকল ছাত্রদের জন্য বাধ্যতামূলক ছিল। বিংশ শতকের আগ পর্যন্ত সমস্ত শিক্ষিত সম্প্রদায়ই এ বইটি পড়েছে বলে ধরে নেয়া হয়। (সম্পূর্ণ নিবন্ধ...)
• 

  

  
  কেপলার ত্রিভুজ হলো এমন একটি সমকোণী ত্রিভুজ যা সোনালি অনুপাতভিত্তিক একটি গুণোত্তর প্রগমনের অন্তর্ভুক্ত তিনটি বর্গের মাধ্যমে গঠিত হয়।

  
  
  কেপলার ত্রিভুজ হলো এমন একটি বিশেষ সমকোণী ত্রিভুজ যার বাহু তিনটির দৈর্ঘ্য একটি গুণোত্তর প্রগমন গঠন করে, যেখানে এই প্রগমনের সাধারণ অনুপাত হলো ${\sqrt {\varphi }}$ এবং $\varphi =(1+{\sqrt {5}})/2$ হলো সোনালি অনুপাত। কেপলার ত্রিভুজের অনন্য বৈশিষ্ট এই প্রগমনটিকে $1:{\sqrt {\varphi }}:\varphi$ আকারে অথবা, আনুমানিকভাবে 1 : 1.272 : 1.618 আকারেও লেখা যায়। কেপলার ত্রিভুজের বাহুগুলোর ওপর অঙ্কিত বর্গ তিনটির ক্ষেত্রফল পৃথক আরেকটি গুণোত্তর প্রগমন গঠন করে। এটি হচ্ছে ${\displaystyle 1:\varphi$ :\varphi ^{2}} । একই ত্রিভুজের বিকল্প সংজ্ঞার ক্ষেত্রে, দুটি সংখ্যার তিনটি পিথাগোরাসীয় গড়ের শর্তালোকে অথবা, সমদ্বিবাহু ত্রিভুজের অন্তর্ব্যাসার্ধের মাধ্যমে এই ত্রিভুজের বৈশিষ্ট্য নির্ধারণ করা হয়।
  
  জ্যোতির্বিদ জোহানেস কেপলারের নামানুসারে এই ত্রিভুজের নামকরণ করা হলেও তার পূর্বেকার নথি বা সূত্রগুলোতেও এর অস্তিত্ব পাওয়া যায়। কিছু সূত্র মোতাবেক প্রাচীন মিশরীয় পিরামিডগুলোতে কেপলার ত্রিভুজভিত্তিক অনুপাত থাকার দাবি করা হলেও, মিশরীয় গণিত ও স্থাপত্যবিদ্যায় সোনালি অনুপাত অজানা ছিল বলেই অধিকাংশ পণ্ডিতের বিশ্বাস। (সম্পূর্ণ নিবন্ধ...)
• 

  

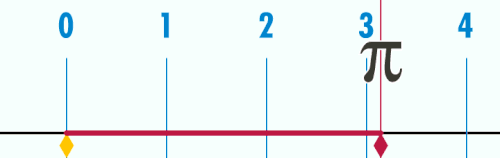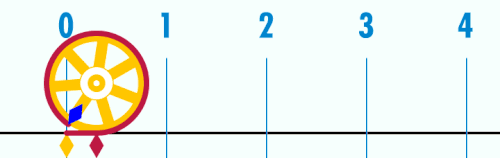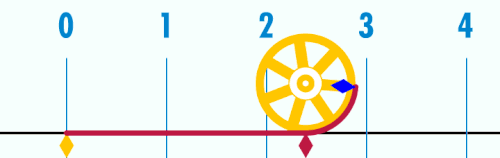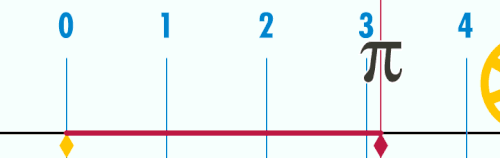
  যখন বৃত্তের ব্যাস ১, এর পরিধি হয় π এর সমান (৩.১৪১৫৯...)।

  
  পাই (ইংরেজি: Pi; প্রতীক π, প্রাচীন গ্রিক ভাষায় পি) একটি গুরুত্বপূর্ণ গাণিতিক ধ্রুবক, মোটামুটিভাবে এর মান প্রায় ৩.১৪১৫৯২৬৫.....। ইউক্লিডীয় জ্যামিতিতে যেকোনো বৃত্তের পরিধি ও ব্যাসের অনুপাতকে এই ধ্রুবক দ্বারা প্রকাশ করা হয়। তবে একইভাবে এটি বৃত্তের ক্ষেত্রফলের সঙ্গে এর ব্যাসার্ধের বর্গের অনুপাতের সমান। গণিত, বিজ্ঞান ও প্রকৌশল বিদ্যার অনেক সূত্রে পাইয়ের দেখা পাওয়া যায়।
  
  পাই একটি অমূলদ সংখ্যা, অর্থাৎ এটিকে দুইটি পূর্ণসংখ্যার ভগ্নাংশ আকারে প্রকাশ করা যায় না। অন্যভাবে বলা যায় এটিকে দশমিক আকারে সম্পূর্ণ প্রকাশ করা সম্ভব নয়। তার মানে আবার এই নয় যে, এটিতে কিছু অঙ্ক পর্যাবৃত্ত বা পৌনঃপুনিক আকারে আসে। বরং দশমিকের পরের অঙ্কগুলো দৈবভাবেই পাওয়া যায়। পাই যে কেবল অমূলদ তা নয়, এটি একই সঙ্গে একটি তুরীয় সংখ্যা, অর্থাৎ এটিকে কোনও বহুপদী সমীকরণের মূল হিসাবেও গণনা করা যায় না। গণিতের ইতিহাস জুড়ে, নির্ভুলভাবে পাইয়ের মান নির্ণয়ের ব্যাপক চেষ্টা করা হয়েছে। এমনকি, এই ধরনের প্রচেষ্টা কখনও কখনও সংস্কৃতির অংশও হয়েছে। (সম্পূর্ণ নিবন্ধ...)
• 

  একটি সুষম ত্রিভুজ

  
  ত্রিভুজ হল এমন একটি বহুভুজ যার তিনটি বাহু এবং তিনটি শীর্ষবিন্দু রয়েছে। এটি জ্যামিতির মূল আকারগুলির মধ্যে একটি। A, B, এবং C শীর্ষবিন্দুসহ একটি ত্রিভুজকে $\triangle ABC$ দ্বারা প্রকাশ করা হয়।
  
  ইউক্লিডীয় জ্যামিতিতে, যেকোন তিনটি বিন্দু, যখন অসমরেখ, একটি অনন্য ত্রিভুজ এবং একই সাথে একটি অনন্য সমতল (অর্থাৎ একটি দ্বি-মাত্রিক ইউক্লিডীয় স্থান) নির্ধারণ করে। অর্থাৎ, শুধু একটিই সমতল রয়েছে যা সেই ত্রিভুজটিকে ধারণ করে এবং প্রতিটি ত্রিভুজই কোনো না কোনো সমতলে রয়েছে। যদি পুরো জ্যামিতিটি শুধু ইউক্লিডীয় সমতলে থাকে, তবে সমস্ত ত্রিভুজ শুধু ওই একটি সমতলেই অবস্থান করছে; যদিও, উচ্চ-মাত্রিক ইউক্লিডীয় স্থানগুলিতে, এই তত্ত্বটি আর সত্য নয়। এই নিবন্ধটি ইউক্লিডীয় জ্যামিতির ত্রিভুজ সম্পর্কে, এবং বিশেষ করে, ইউক্লিডীয় সমতল, যদি অন্যরূপে উল্লেখিত না থাকে। (সম্পূর্ণ নিবন্ধ...)

উল্লিখিত তথ্যগুলি উইকিপিডিয়া:আপনি জানেন কি প্রকল্পের অংশ হিসেবে প্রধান পাতায় প্রদর্শিত হয়েছে।

---

• ... শূন্য একটি জোড় সংখ্যা?
• ... ৩ এর চেয়ে বড় সকল মৌলিক সংখ্যার বর্গের পূর্ববর্তী সংখ্যা ১২ দ্বারা বিভাজ্য?
• ... ২০০৯ সালের হিসাব অনুযায়ী জ্ঞাত সর্ববৃহৎ মৌলিক সংখ্যায় ১৩০ লক্ষ অঙ্ক আছে?
• ... ইতালীয় গণিতবিদ জিরোলামো কার্দানো ত্রিঘাত সমীকরণ সমাধান করতে গিয়ে জটিল সংখ্যা আবিস্কার করেন?
• ... গ্রিক গণিতবিদ ইউক্লিড রচিত মৌলিক উপাদানসমূহ বইটি প্রায় ২০০০ বছর ধরে জ্যামিতি শিক্ষায় মূল্য পাঠ্য হিসেবে ব্যবহৃত হয়েছে?
• ... সুইজারল্যান্ডীয় গণিতবিদ লিওনার্ট অয়লার ১৭৬৬ সালে পুরোপুরি অন্ধ হয়ে যাবার পরও ১৭৭৫ সালে প্রায় প্রতি সপ্তাহে একটি করে গাণিতিক গবেষণা প্রবন্ধ রচনা করতেন?
• ... ৬১৭৪ সংখ্যাটি নিয়ে গণিতবিদ ডি. আর. কাপরেকারেরগবেষণার জন্য সংখ্যাটিকে তার নামানুসারে "কাপরেকার ধ্রুবক" বলে ডাকা হয়?
• ... জার্মান গণিতবিদ কার্ল ফ্রিড‌রিশ গাউস ১৭৯৮ সালে মাত্র ২১ বছর বয়সে তাঁর জীবনের সর্বশ্রেষ্ঠ কাজ ডিসকিশিয়নেস অ্যারিথমেটিকা রচনা করেন?
• ... মুখস্থভাবে গাণিতিক ধ্রুবক পাইয়ের মান বলাতে গিনেসের স্বীকৃতিপ্রাপ্ত রেকর্ড হল দশমিক বিন্দুর পরে ৬৭,৮৯০ ঘর পর্যন্ত, যার অধিকারী চীনের ২৪ বছর বয়স্ক স্নাতক ছাত্র লু চাও?
• ...আন্তর্জাতিক গণিত অলিম্পিয়াডে যেসব প্রতিযোগী কোনো পদক জয় করতে পারে না, কিন্তু কোনো সমস্যায় সাত নম্বর পায় তাঁদেরও সম্মানজনক উদ্ধৃতি প্রদান করা হয়?

• 

  আইজ্যাক নিউটনের প্রতিকৃতি, ১৬৮৯

  
  স্যার আইজাক নিউটন (ইংরেজি: Sir Isaac Newton; ৪ জানুয়ারি ১৬৪৩ - ৩১ মার্চ ১৭২৭) প্রখ্যাত ইংরেজ পদার্থবিজ্ঞানী, গণিতবিদ, জ্যোতির্বিজ্ঞানী, প্রাকৃতিক দার্শনিক এবং আলকেমিস্ট।স্যার আইজাক নিউটন সর্বকালের সর্বযুগের সর্বশ্রেষ্ঠ এবং সবচেয়ে প্রভাবশালী বিজ্ঞানী। ১৬৮৭ খ্রিস্টাব্দে তার বিশ্ব নন্দিত গ্রন্থ ফিলোসফিয়া ন্যাচারালিস প্রিন্সিপিয়া ম্যাথামেটিকা প্রকাশিত হয় যাতে তিনি সর্বজনীন মহাকর্ষ এবং গতির তিনটি সূত্র প্রমাণ করেছিলেন। এই সূত্র ও মৌল নীতিগুলোই চিরায়ত বলবিজ্ঞানের ভিত্তি হিসেবে কাজ করেছে, আর তার গবেষণার ফলে উদ্ভূত এই চিরায়ত বলবিজ্ঞান পরবর্তী তিন শতক জুড়ে বৈজ্ঞানিক চিন্তাধারার জগতে একক আধিপত্য করেছে। তিনিই প্রথম দেখিয়েছিলেন, পৃথিবী এবং মহাবিশ্বের সকল বস্তু একই প্রাকৃতিক নিয়মের অধীনে পরিচালিত হচ্ছে। কেপলারের গ্রহীয় গতির সূত্রের সাথে নিজের মহাকর্ষ তত্ত্বের সমন্বয় ঘটিয়ে তিনি এর সুস্পষ্ট ব্যাখ্যা দিতে সমর্থ হয়েছিলেন। তার গবেষণার ফলেই সৌরকেন্দ্রিক বিশ্বের ধারণার পেছনে সামান্যতম সন্দেহও দূরীভূত হয় এবং বৈজ্ঞানিক বিপ্লব ত্বরান্বিত হয়।
  
  বলবিজ্ঞানের ভিত্তিভূমি রচনা করেছেন নিউটন। রৈখিক এবং কৌণিক ভরবেগের সংরক্ষণ সূত্রের মাধ্যমে তিনি এই ভিত্তি রচনা করেন। আলোকবিজ্ঞানের কথায় আসলে তার হাতে তৈরি প্রতিফলন দূরবীক্ষণ যন্ত্রের কথা এসে যায়। একই সাথে তিনি আলোর বর্ণের উপরএকটি তত্ত্ব দাড় করান যা একটি পর্যবেক্ষণের মাধ্যমে তিনি নিশ্চিত হয়েছিলেন। পর্যবেক্ষণটি ছিল ত্রিভুজাকার প্রিজমের মধ্য দিয়ে যাওয়া আলোর বিক্ষেপণের উপর যার মাধ্যমে দৃশ্যমান বর্ণালির সৃষ্টি হয়েছিল। শব্দের দ্রুতি এবং শীতলীকরণ প্রক্রিয়া বিষয়েও তিনি গবেষণা পরিচালনা করেন যা থেকে নিউটনের শীতলীকরণ সূত্র এসেছে। (সম্পূর্ণ নিবন্ধ...)
• 

  সত্যেন্দ্রনাথ বসু

  
  সত্যেন্দ্রনাথ বসু (১লা জানুয়ারি ১৮৯৪ – ৪ঠা ফেব্রুয়ারি ১৯৭৪) ছিলেন একজন বাঙালি পদার্থবিজ্ঞানী। তার গবেষণার ক্ষেত্র ছিল গাণিতিক পদার্থবিজ্ঞান। সত্যেন্দ্রনাথ বসু আলবার্ট আইনস্টাইনের সঙ্গে যৌথভাবে বোস-আইনস্টাইন পরিসংখ্যান প্রদান করেন, যা পদার্থবিজ্ঞানের অন্যতম গুরুত্বপূর্ণ আবিষ্কার বলে বিবেচিত হয়। ছাত্রজীবনে অত্যন্ত মেধাবী সত্যেন্দ্রনাথ কর্মজীবনে সংযুক্ত ছিলেন বৃহত্তর বাংলার শ্রেষ্ঠ শিক্ষায়তন ঢাকা বিশ্ববিদ্যালয়, কুমিল্লা ভিক্টোরিয়া সরকারি কলেজ, কলকাতা বিশ্ববিদ্যালয় ও বিশ্বভারতী বিশ্ববিদ্যালয়ের সঙ্গে। সান্নিধ্য পেয়েছেন রবীন্দ্রনাথ ঠাকুর, প্রফুল্লচন্দ্র রায়, মারি ক্যুরি প্রমুখ মনীষীর। আবার অনুশীলন সমিতির সঙ্গে প্রত্যক্ষ সম্পর্ক ও স্বাধীনতা আন্দোলনের সশস্ত্র বিপ্লবীদের সঙ্গে গোপনে যোগাযোগও রাখতেন দেশব্রতী সত্যেন্দ্রনাথ। কলকাতায় জাত সত্যেন্দ্রনাথ শুধুমাত্র বাংলায় বিজ্ঞানচর্চার প্রবল সমর্থকই ছিলেন না, সারা জীবন ধরে তিনি বাংলায় বিজ্ঞানচর্চার ধারাটিকেও পুষ্ট করে গেছেন। এই প্রসঙ্গে তার অমর উক্তি,

  “ যারা বলেন বাংলা ভাষায় বিজ্ঞান চর্চা হয় না, তারা হয় বাংলা জানেন না, নয় বিজ্ঞান বোঝেন না। ”

  বাংলায় বিজ্ঞানচর্চার প্রসারের উদ্দেশ্যে বিজ্ঞান পরিচয় নামে একটি পত্রিকাও প্রকাশ করেন তিনি। ব্যক্তিজীবনে সত্যেন্দ্রনাথ ছিলেন নিরলস, কর্মঠ ও মানবদরদী মনীষী। বিজ্ঞানের পাশাপাশি সঙ্গীত ও সাহিত্যেও ছিল তার আন্তরিক আগ্রহ ও বিশেষ প্রীতি। রবীন্দ্রনাথ তাকে নিজের বিশ্বপরিচয় বিজ্ঞানগ্রন্থ, অন্নদাশঙ্কর রায় তার জাপানে ভ্রমণরচনা ও সুধীন্দ্রনাথ দত্ত তার অর্কেস্ট্রা কাব্যগ্রন্থ উৎসর্গ করেছিলেন। (সম্পূর্ণ নিবন্ধ...)
• 

  

  
  আবু রায়হান আল-বেরুনী বা আবু রায়হান মুহাম্মাদ ইবনে আহমদ আল-বেরুনী (ফার্সি: ابوریحان محمد بن احمد بیرونی; ৯৭৩–১০৪৮), সাধারণত আল-বেরুনী নামে পরিচিত, ইসলামী স্বর্ণযুগে একজন খাওয়ারেজমিয় ইরানি পণ্ডিত এবং বহুবিদ্যাবিশারদ ছিলেন। তাকে বিভিন্নভাবে " ইন্ডোলজির প্রতিষ্ঠাতা", " তুলনামূলক ধর্মের জনক", "আধুনিক জিওডেসির জনক " এবং প্রথম নৃতত্ত্ববিদ বলা হয়। তিনি অত্যন্ত মৌলিক ও গভীর চিন্তধারার অধিকারী ছিলেন। শহরের বাইরে বসবাস করতেন বলে সাধারণভাবে তিনি আল-বেরুনী নামে পরিচিত। রুশীয় তুর্কিস্তানের খিওয়ায় এটি অবস্থিত ছিলো। শহরটি খাওয়ারিজিমের রাজধানীর কাছে ছিলো। বর্তমানে শহরটি নদীতে বিলীন হয়ে গিয়েছে। এখন এ স্থানটি আল-বেরুনী শহর নামে অভিহিত। তিনি ছিলেন গণিত, জ্যোতিঃপদার্থবিদ, রসায়ন ও প্রাকৃতিক বিজ্ঞানে পারদর্শী। অধিকন্তু ভূগোলবিদ, ঐতিহাসিক, পঞ্জিকাবিদ, দার্শনিক এবং চিকিৎসা বিজ্ঞান, ভাষাতত্ত্ববিদ ও ধর্মতত্ত্বের নিরপেক্ষ বিশ্লেষক। স্বাধীন চিন্তা, মুক্তবুদ্ধি, সাহসিকতা, নির্ভীক সমালোচক ও সঠিক মতামতের জন্য যুগ শ্রেষ্ঠ বলে স্বীকৃত। হিজরি চতুর্থ শতাব্দীর শেষার্ধ ও পঞ্চম শতাব্দীর প্রথমার্ধকে আল-বেরুনীর কাল বলে উল্লেখ করা হয়। তিনি সর্বপ্রথম প্রাচ্যের জ্ঞানবিজ্ঞান, বিশেষ করে ভারতের জ্ঞান-বিজ্ঞানের প্রতি মুসলিম মনীষীদের দৃষ্টি আকর্ষণ করেছিলেন। অধ্যাপক মাপা বলেন, "আল-বেরুনী শুধু মুসলিম বিশ্বেরই নন, বরং তিনি ছিলেন সমগ্র বিশ্বের শ্রেষ্ঠ জ্ঞানীদের একজন।”
  
  আল-বেরুনী পদার্থবিদ্যা, গণিত, জ্যোতির্বিদ্যা এবং প্রাকৃতিক বিজ্ঞানে পারদর্শী ছিলেন এবং একজন ইতিহাসবিদ, কালানুক্রমিক এবং ভাষাবিদ হিসেবেও নিজেকে আলাদা করেছিলেন। তিনি তার দিনের প্রায় সমস্ত বিজ্ঞান অধ্যয়ন করেছিলেন এবং জ্ঞানের অনেক ক্ষেত্রে তার অক্লান্ত গবেষণার জন্য প্রচুর পুরস্কৃত হয়েছিলো। রাজা এবং সমাজের অন্যান্য শক্তিশালী উপাদান আল-বেরুনীর গবেষণাকে অর্থায়ন করে এবং নির্দিষ্ট প্রকল্পের কথা মাথায় রেখে তাকে খুঁজে বের করে। নিজের অধিকারে প্রভাবশালী, আল-বেরুনী নিজে অন্যান্য জাতির পণ্ডিতদের দ্বারা প্রভাবিত ছিলেন, যেমন গ্রীক, যাদের থেকে তিনি অনুপ্রেরণা নিয়েছিলেন যখন তিনি দর্শনের অধ্যয়নের দিকে মনোনিবেশ করেছিলেন। একজন প্রতিভাধর ভাষাবিদ, তিনি খওয়ারেজমিয়ান, ফার্সি, আরবি, সংস্কৃত এবং গ্রীক, হিব্রু এবং সিরিয়াক ভাষাও জানতেন। তিনি তার জীবনের বেশিরভাগ সময় কাটিয়েছেন গজনীতে, তৎকালীন গজনভিদের রাজধানী, আধুনিক দিনের মধ্য-পূর্ব আফগানিস্তানে। ১০১৭ সালে তিনি ভারতীয় উপমহাদেশে ভ্রমণ করেন এবং ভারতে প্রচলিত হিন্দু ধর্মের অন্বেষণের পর তারিখ আল-হিন্দ (ভারতের ইতিহাস) শিরোনামে ভারতীয় সংস্কৃতির উপর একটি গ্রন্থ রচনা করেন। তিনি তার সময়ের জন্য, বিভিন্ন জাতির রীতিনীতি এবং ধর্মের উপর একজন প্রশংসনীয়ভাবে নিরপেক্ষ লেখক ছিলেন, ১১ শতকের প্রথম দিকে ভারত তার পাণ্ডিত্যপূর্ণ বস্তুনিষ্ঠতা তাকে আল-ওস্তাদ ("দ্য মাস্টার") উপাধি অর্জন করেছিল তার প্রথম দিকের অসাধারণ বর্ণনার স্বীকৃতিস্বরূপ। (সম্পূর্ণ নিবন্ধ...)
• 

  ইয়োহান কার্ল ফ্রিড্‌রিশ গাউস (১৭৭৭–১৮৫৫), ক্রিস্তিয়ান আলব্রেশট জেনসেন অঙ্কিত।

  
  ইয়োহান কার্ল ফ্রিডরিশ গাউস (: ইয়োহান্‌ কাল্‌ ফ্রিড্‌রিশ্‌ গাউস্‌; জার্মান ভাষায়: Johann Carl Friedrich Gauß) (৩০শে এপ্রিল, ১৭৭৭ - ২৩শে ফেব্রুয়ারি, ১৮৫৫) একজন প্রতিভাবান জার্মান গণিতবিদ এবং বিজ্ঞানী। গণিত ও বিজ্ঞানের প্রায় সকল বিভাগে তার অবদান আছে। তাকে "গণিতের যুবরাজ" ও "সর্বকালের সেরা গণিতবিদ" বলা হয়। গণিতের যে সব বিষয়ে তার অবদান আছে সেগুলোর মধ্যে আছে সংখ্যা তত্ত্ব, গাণিতিক বিশ্লেষণ, অন্তরক জ্যামিতি, চুম্বকের ধর্ম, আলোকবিজ্ঞান, জ্যোতির্বিজ্ঞান ইত্যাদি। গণিত এবং বিজ্ঞানের বহু শাখায় তার প্রশংসাযোগ্য প্রভাব ছিল, যে কারণে তাকে ইতিহাসের অন্যতম প্রভাবশালী গণিতবিদদের একজন হিসেবে বিবেচনা করা হয়।
  
  গাউস ছোটবেলা থেকেই অসম্ভব প্রতিভাবান ছিলেন । ছোটবেলার তার গাণিতিক প্রতিভা নিয়ে অনেক গল্প শোনা যায়। তিনি কৈশোরেই তার প্রথম গুরুত্বপূর্ণ গাণিতিক আবিষ্কারগুলো সম্পাদন করেন। ১৭৯৮ সালে মাত্র ২১ বছর বয়সে তিনি তার জীবনের সর্বশ্রেষ্ঠ কাজ ডিসকিশিয়নেস অ্যারিথমেটিকা লেখা সমাপ্ত করেন, যা ১৮০১ সালে প্রকাশিত হয়। তার এই কাজ গণিতের একটি পৃথক শাখা হিসেবে সংখ্যাতত্ত্বের ভিত্তি স্থাপন করে এবং আজও এর প্রভাব অপরিসীম। (সম্পূর্ণ নিবন্ধ...)
• 

  কাঠের কারুকাজে আল খোয়ারিজমিকে অঙ্কন, বিংশ শতাব্দী

  
  মুহাম্মাদ বিন মুসা আল খোয়ারিজমি (আরবি: محمد بن موسى الخوارزمي; আনু. ৭৮০–৮৫০) ছিলেন একজন ফার্সি বহুবিদ্যাবিশারদ, যিনি গণিত, জ্যোতির্বিজ্ঞান এবং ভূগোলের ক্ষেত্রে ব্যাপকভাবে প্রভাবশালী অবদান রেখেছিলেন। তিনি আল খারেজমি, আল খাওয়ারেজমি বা আল খোয়ারিজমি নামেও সমধিকভাবে পরিচিত। মূলত অ্যালগরিদম ও আলজেবরা যথাক্রমে তার নামের ভুল লাতিনিকরণ আলোগোরিদমি ও তার গ্রন্থ আল-জাবর থেকে প্রাপ্ত। আনুমানিক ৮২০ সালে তিনি আব্বাসীয় খিলাফতের রাজধানী বাগদাদের বাইতুল হিকমাহ গ্রন্থাগারের জ্যোতির্বিজ্ঞানী এবং প্রধান হিসেবে নিযুক্ত হন।
  
  বীজগণিতের উপর আল খোয়ারিজমির জনপ্রিয় গ্রন্থ আল-জাবর রৈখিক এবং দ্বিঘাত সমীকরণের প্রথম পদ্ধতিগত সমাধান উপস্থাপন করেছিল। বীজগণিতে তার অন্যতম প্রধান সাফল্য ছিল বর্গক্ষেত্রটি সম্পূর্ণ করে কীভাবে দ্বিঘাত সমীকরণগুলি সমাধান করা যায় তার প্রদর্শন, যার জন্য তিনি জ্যামিতিক যৌক্তিকতা সরবরাহ করেছিলেন। কারণ তিনিই প্রথম বীজগণিতকে একটি স্বাধীন শৃঙ্খলা হিসেবে গণ্য করেন এবং "হ্রাস" এবং "ভারসাম্য" পদ্ধতি (বিয়োগকৃত পদগুলির একটি সমীকরণের অন্য দিকে স্থানান্তর, অর্থাৎ, সমীকরণের বিপরীত দিকের অনুরূপ পদ বাতিল করা) প্রবর্তন করেন, আল-খারেজমিকেই বীজগণিতের জনক বা প্রতিষ্ঠাতা হিসাবে বর্ণনা করা হয়। বীজগণিত শব্দটি নিজেই তার বইয়ের শিরোনাম থেকে এসেছে (আল-জাবের শব্দের অর্থ "সমাপ্তি" বা "পুনরায় যোগদান")। তার নাম অ্যালগোরিজম এবং অ্যালগরিদম শব্দের জন্ম দেয়, সেইসাথে স্প্যানিশ, ইতালীয় এবং পর্তুগিজ শব্দ অ্যালগোরিটমো, এবং স্প্যানিশ গুয়ারিস্মো এবং পর্তুগিজ আলগারিস্মো অর্থ "ডিজিট"। (সম্পূর্ণ নিবন্ধ...)
• 

  

  
  কার্ল থিওডোর উইলহেলম উইয়েরস্ট্রাস (German:Weierstraß [ˈvaɪɐʃtʁaːs]; ৩১শে অক্টোবর ১৮১৫ - ১৯শে ফেব্রুয়ারি ১৮৯৭) ছিলেন একজন স্বনামধন্য জার্মান গণিত বিশেষজ্ঞ যাঁকে আধুনিক বিশ্লেষণ(মডার্ন অ্যানালাইসিস)-এর জনক বলা হয়। কোনো প্রথাগত ডিগ্রি ছাড়া বিশ্ববিদ্যালয় থেকে বেরিয়ে আসা সত্ত্বেও তিনি গণিত নিয়ে যথাযথ পড়াশোনা করেন এবং তার সাথে স্কুল-শিক্ষক হওয়ার প্রশিক্ষণও গ্রহণ করেন। গণিতের পাশাপাশি তিনি ভৌতবিদ্যা, উদ্ভিদবিদ্যা, শরীর-কলাবিদ্যা ইত্যাদি বিষয়েও শিক্ষা প্রদান করেন। পরবর্তীকালে তিনি সম্মানীয় ডক্টরেট উপাধি লাভ করেন এবং বার্লিনে গণিতের অধ্যাপক হিসেবে প্রভূত সম্মান লাভ করেন।
  
  ওনার অসংখ্য অবদানের মধ্যে উলেখ্য জটিল বিশ্লেষণ (কমপ্লেক্স অ্যানালাইসিস) এবং ফাংশনের ধারাবাহিকতার সংজ্ঞা গঠন। এছাড়াও উনি মধ্যবর্তী মান উপপাদ্য (ইন্টারমিডিয়েট ভ্যালু থিওরেম) ও বোলজানো উইয়েরস্ট্রাস থিওরেম প্রমাণ করেন এবং বলজানো উইয়েরস্ট্রাস উপপাদ্যের সাহায্যে বন্ধ আবদ্ধ বন্ধনীতে (ক্লোজড বাউন্ডেড ইন্টারভ্যাল) ধারাবাহিক ফাংশনের বিভিন্ন বৈশিষ্ট্য নিয়ে পর্যবেক্ষণ করেন। (সম্পূর্ণ নিবন্ধ...)
• 

  জ্যাকব ইমানুয়েল হান্ডম্যান দ্বারা পোর্ট্রেট করা হয়েছে (১৭৫৩)

  
  লেওনার্ড অয়লার (জার্মান: Leonhard Euler — উচ্চারণ: [ˈleonaɐt ˈɔʏlɐ], লেওনাআট্‌ অয়লা ) (আ-ধ্ব-ব: [ˈleonaɐt ˈɔʏlɐ]) (১৫ এপ্রিল, ১৭০৭, বাসেল, সুইজারল্যান্ড - ১৮ই সেপ্টেম্বর, ১৭৮৩, সেন্ট পিটার্সবার্গ, রাশিয়া) একজন সুইস গণিতবিদ এবং পদার্থবিজ্ঞানী। তিনি ক্যালকুলাস, সংখ্যাতত্ত্ব, অন্তরক সমীকরণ, গ্রাফ তত্ত্ব ও টপোগণিতে অনেক গুরুত্বপূর্ণ অবদান রাখেন। আধুনিক গণিতে ব্যবহৃত অনেক পরিভাষা ও ধারণা তার অবদান। গাণিতিক বিশ্লেষণে ব্যবহৃত গাণিতিক ফাংশন-এর ধারণা তারই আবিষ্কার। অয়লার e , পাই এর জন্য π , যোগের জন্য Σ চিহ্নের প্রবর্তন করেন। তিনি বলবিজ্ঞান, আলোকবিজ্ঞান ও জ্যোতির্বিজ্ঞানেও অবদান রাখেন। সমসাময়িককালে তার মতো প্রকাশনা সম্পন্ন কোনো গণিতবিদ ছিলেন না। এমনকি মুদ্রণ ব্যবস্থার উন্নতি হওয়ার পরও তার সমপরিমাণ প্রকাশনা সম্পন্ন বিজ্ঞানীর সংখ্যা খুবই কম।
  
  অয়লারকে ১৮শ শতকের সেরা গণিতবিদ ও সর্বকালের সেরা গণিতবিদদের একজন বলে মনে করা হয়। গণিতবিদদের মধ্যে তার প্রকাশিত গবেষণা কাজের পরিমাণ আজও সর্বাধিক এবং এটি একটি গিনেস রেকর্ড। বলা হয় তার সম্পর্কে লাপ্লাস বলেছিলেন: "Lisez Euler, lisez Euler, c'est notre maître à tous" ("অয়লার পড়, অয়লার পড়, তিনি আমাদের সবার শিক্ষক।")। 2002 Euler নামের গ্রহাণুটি তার সম্মানে নামকরণ করা হয়। সুইস ১০-ফ্রা এর নোট এবং সুইজারল্যান্ড, রাশিয়া ও জার্মানির অসংখ্য ডাকটিকেটে তার ছবি রয়েছে। (সম্পূর্ণ নিবন্ধ...)
• 

  চিন্তিত আর্কিমিডিস; চিত্রকর Domenico Fetti (১৬২০)

  
  আর্কিমিডিস (প্রাচীন গ্রিক ভাষায়: Ἀρχιμήδης আর্খিম্যাদ্যাস্‌, বর্তমান গ্রিক ভাষায় Αρχιμήδης আর্খ়িমিদ়িস্‌) বা সিরাকাসের আর্কিমিডিস (খ্রি.পূ. ২৮৭-২১২) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক।
  প্রাচীন গ্রিক সভ‍্যতা তার উন্নতির সর্বোচ্চ শিখরে পৌছেছিলো প্রাচীন কালের সর্বশ্রেষ্ঠ গণিতজ্ঞ আর্কিমিডিস এর সময়ে। যদিও তার জীবন সম্পর্কে খুব কমই জানা গেছে, তবুও তাকে ক্ল্যাসিক্যাল যুগের অন্যতম সেরা বিজ্ঞানী হিসেবে বিবেচনা করা হয়। পদার্থবিদ্যায় তার উল্লেখযোগ্য অবদানের মধ্যে রয়েছে স্থিতিবিদ্যা আর প্রবাহী স্থিতিবিদ্যার ভিত্তি স্থাপন এবং লিভারের কার্যনীতির বিস্তারিত ব্যাখ্যাপ্রদান। পানি তোলার জন্য আর্কিমিডিসের স্ক্রু পাম্প, যুদ্ধকালীন আক্রমণের জন্য সীজ (ইংরেজি: siege সীঝ়্‌) ইঞ্জিন ইত্যাদি মৌলিক যন্ত্রপাতির ডিজাইনের জন্যও তিনি বিখ্যাত। আধুনিক বৈজ্ঞানিক পরীক্ষায় তার নকশাকৃত আক্রমণকারী জাহাজকে পানি থেকে তুলে ফেলার যন্ত্র বা পাশাপাশি রাখা একগুচ্ছ আয়নার সাহায্যে জাহাজে অগ্নিসংযোগের পদ্ধতি সফলভাবে বাস্তবায়ন করা সম্ভব হয়েছে।
  
  আর্কিমিডিসকে সাধারণত প্রাচীন যুগের সেরা এবং সর্বাকালের অন্যতম সেরা গণিতজ্ঞ হিসেবে বিবেচনা করা হয়। তিনি মেথড অফ এক্সহশন ব্যবহার করে অসীম ধারার সমষ্টিরূপে প্যারাবোলার বক্ররেখার অন্তগর্ত ক্ষেত্রের ক্ষেত্রফল নির্ণয় করেন এবং পাই -এর প্রায় নিখুঁত একটি মান নির্ণয় করেন। এছাড়াও তিনি আর্কিমিডিসের স্পাইরালের সংজ্ঞা দেন, বক্রতলের ক্ষেত্রফল নির্ণয়ের সূত্র প্রদান করেন এবং অনেক বড় সংখ্যাকে সহজে প্রকাশ করার একটি চমৎকার পদ্ধতি আবিষ্কার করেন। (সম্পূর্ণ নিবন্ধ...)
• 

  

  
  হাসান ইবনে আল-হায়সাম (ল্যাটিনকৃত: আলহাজেন ; /ælˈhæzən/; লাতিন: Alhazen; পূর্ণ নামঃ আরবি: أبو علي، الحسن بن الحسن بن الهيثم, প্রতিবর্ণীকৃত: আবু আলি হাসান ইবনুল হাসান ইবনুল হায়সাম, অনুবাদ 'Abū ʿAlī al-Ḥasan ibn al-Ḥasan ibn al-Haytham'; আনু. ৯৬৫ – আনু. ১০৪০), ছিলেন ইসলামী স্বর্ণযুগের একজন মুসলিম আরব গণিতবিদ, জ্যোতির্বিজ্ঞানী এবং পদার্থবিদ। তিনি "আধুনিক আলোকবিজ্ঞানের জনক" হিসেবে উল্লেখিত হন, আলোকবিদ্যার নীতি এবং বিশেষ করে দর্শনানুভূতির ব্যাখ্যায় তিনি গুরুত্বপূর্ণ অবদান রেখেছিলেন। তার সর্বাপেক্ষা প্রভাবশালী কাজ হচ্ছে তার কিতাবুল মানাজির ("আলোকবিদ্যার গ্রন্থ", আরবি: كتاب المناظر), যা ১০১১–১০২১ সালের মধ্যে লেখা এবং লাতিন সংস্করণে বিস্তার লাভ করেছিল অনুমান করা হয়। তিনি একজন বহুবিদ্যাবিশারদ ছিলেন, যিনি একাধারে দর্শন, ধর্মতত্ত্ব ও চিকিৎসাশাস্ত্রের সম্পর্কেও বিশেষ অবদান রেখেছেন।
  
  ইবনে আল-হায়সাম ছিলেন যিনি দর্শনানুভূতির ব্যাখ্যার সর্বপ্রথম প্রমাণ দিতে সক্ষম হয়েছিলেন, যে 'আলো কোন বস্তু হইতে প্রতিফলিত হয়ে চোখে আসে বলেই সেই বস্তুটি দৃশ্যমান হয়'। এছাড়াও তিনিই প্রথম যিনি এটাও দেখিয়ে ছিলেন, দর্শনানুভূতির কেন্দ্র চোখে নয়, বরং মস্তিষ্কে। তিনি তার এই তত্ত্বের অনুপ্রেরণা পেয়েছিলেন গ্রিক দার্শনিক অ্যারিস্টটলের কাছ থেকে। তিনি আধুনিক বৈজ্ঞানিক পদ্ধতির একজন প্রাচীনতম প্রবক্তা, যে তত্ত্ব ও অনুমান অবশ্যই পুনরায় পরিচালনাযোগ্য পরীক্ষণের মাধ্যমে নিশ্চিত হতে হয়, এতে তিনি রেনেসাঁর পণ্ডিতগণের পাঁচ শতাব্দী পূর্বেই বৈজ্ঞানিক তত্ত্বের পরিপূর্ণ ও স্পষ্ট বর্ণনাদাতার মর্যাদা পান। এ কারণের জন্যই, তাকে কখনও কখনও বিশ্বের "প্রথম সত্যিকারের বিজ্ঞানী" হিসাবে বর্ণনা করা হয়। (সম্পূর্ণ নিবন্ধ...)
• 

  ১৯২৭ সালে হার্ডি

  
  গডফ্রি হ্যারল্ড হার্ডি এফআরএস (৭ ফেব্রুয়ারি ১৮৭৭ - ০১ ডিসেম্বর ১৯৪৭) ছিলেন একজন ইংরেজ গণিতবিদ। তিনি সংখ্যা তত্ত্ব এবং গাণিতিক বিশ্লেষণের উপর উল্লেখযোগ্য অবদানের জন্য পরিচিত ছিলেন। জীববিজ্ঞানে, তিনি হার্ডি-উইনবার্গ নীতির জন্য পরিচিত। এটি জনসংখ্যা বংশাণুবিজ্ঞানের একটি মৌলিক নীতি। গণিতের বাইরেও জিএইচ হার্ডি ১৯৪০ সালে তার রচিত প্রবন্ধ এ ম্যাথমেটিশিয়ান'স অ্যাপোলজি-এর জন্য পরিচিত।
  
  ১৯১৪ সালে, হার্ডি বিখ্যাত ভারতীয় গণিতবিদ শ্রীনিবাস রামানুজনের পরামর্শদাতা হয়েছিলেন। হার্ডি রামানুজনের অসাধারণ বুদ্ধিমত্তা সম্পর্কে ধারণা করতে পেরেছিলেন এবং হার্ডি ও রামানুজন একে অপরের ঘনিষ্ঠ সহযোগী হয়ে ওঠেন। পল এর্ডশকে দেওয়া একটি সাক্ষাৎকারে হার্ডিকে জিজ্ঞাসা করা হয়েছিল, গণিতে তার সবচেয়ে বড় অবদান কী, হার্ডি নিঃসংকোচে উত্তর দিয়েছিলেন যে গণিতে তার সবচেয়ে বড় অবদান ছিল শ্রীনিবাস রামানুজনকে আবিষ্কার করা। রামানুজনের উপর একটি বক্তৃতায় হার্ডি বলেছিলেন যে "তার সাথে আমার মেলামেশা আমার জীবনের একটি প্রণয়ধর্মী ঘটনা"। (সম্পূর্ণ নিবন্ধ...)
• 

  লুডভিগ এডুয়ার্ড বোলৎসমান (১৮৪৪-১৯০৬)

  
  লুডভিগ এডুয়ার্ড বোলৎসমান (জার্মান: Ludwig Boltzmann) (২০শে ফেব্রুয়ারি, ১৮৪৪ - ৫ই সেপ্টেম্বর, ১৯০৬) প্রখ্যাত অষ্ট্রীয় পদার্থবিজ্ঞানী, দার্শনিক ও গণিতজ্ঞ। তিনিই প্রথম বলেছিলেন, পরমাণুকে না দেখলেও কিছু পরিসাংখ্যিক সমীকরণের মাধ্যমে তাদের গতিবিধি বর্ণনা করা সম্ভব। এভাবেই তিনি পরিসাংখ্যিক গতিবিদ্যার জন্ম দেন। তখনকার প্রতিষ্ঠিত নিয়মের বাইরে গিয়ে তিনি আরও বলেছিলেন, তাপগতিবিদ্যায় সম্ভাব্যতার ধারণা সংযোজন করা উচিত। এভাবে তার হাত ধরে পরিসাংখ্যিক তাপগতিবিদ্যারও জন্ম হয়েছিল। তিনি বুঝতে পেরেছিলেন প্রকৃতির বিশৃঙ্খলাকে এনট্রপি নামক একটি গাণিতিক রাশির মাধ্যমে পরিমাপ করা সম্ভব। সে সময় প্রচলিত ধ্রুব প্রাকৃতিক নিয়মের বিরুদ্ধে গিয়ে প্রকৃতির বাস্তব বিশৃঙ্খলা এবং সম্ভাব্যতার প্রভাব আবিষ্কার করেছিলেন বলেই তাকে বলা হয় দ্য জিনিয়াস অফ ডিসঅর্ডার।
  
  পেশাগত জীবনে আর্নস্ট মাখ-এর মত বিজ্ঞানীদের সক্রিয় বিরোধিতায় তিনি হতাশাগ্রস্ত হয়ে পড়েন। মাখ এবং তার সমর্থকরা পরমাণু পর্যবেক্ষণ করা যায় না বলে তা বিশ্বাস করতেন না, বরং সবকিছু শক্তি দিয়ে ব্যাখ্যার চেষ্টা করতেন। আজীবন মাখ এবং অস্টভাল্ডদের শক্তিবাদ (এনার্জেটিক্স) নামের এই তত্ত্বের বিরোধিতা করেছেন বোলৎসমান। অন্যদিকে ব্যক্তিগত জীবনে তার মা এবং ১১ বছরের ছেলের মৃত্যুতে তিনি ভেঙে পড়েন। মনস্তত্ত্ববিদদের মতে, এই জিনিয়াস অফ ডিসঅর্ডার যে রোগে ভুগছিলেন তার নাম বাইপোলার ডিসঅর্ডার। জার্মানির লাইপৎসিগে একবার আত্মহত্যার চেষ্টা করেন। সবশেষে ১৯০৬ সালে ইতালির ত্রিয়েস্তের নিকটে একটি স্থানে আত্মহত্যার মাধ্যমেই এই মহান বিজ্ঞানীর জীবনাবসান ঘটে। বলা হয় আর ২০ বছর বেঁচে থাকলে তিনি দেখে যেতে পারতেন যে, তার পরমাণু এবং সম্ভাব্যতার প্রতি নিরংকুশ সমর্থনই জয়লাভ করেছে, শক্তিবাদ ছদ্ম-বিজ্ঞান হিসেবে পরিত্যক্ত হয়েছে। (সম্পূর্ণ নিবন্ধ...)
• 

  শ্রীনিবাস রামানুজন (১৮৮৭ - ১৯২০)

  
  শ্রীনিবাস রামানুজন (২২ ডিসেম্বর ১৮৮৭ – ২৬ এপ্রিল ১৯২০) অসামান্য প্রতিভাবান একজন ভারতীয় গণিতবিদ। খুব অল্প সময় বাঁচলেও তিনি গণিতে সুদূরপ্রসারী অবদান রেখে গেছেন। প্রথাগত শিক্ষা না থাকলেও সম্পূর্ণ নিজের প্রচেষ্টায় তিনি গণিতের বিভিন্ন শাখায়, বিশেষ করে গাণিতিক বিশ্লেষণ, সংখ্যাতত্ত্ব, অসীম ধারা ও আবৃত্ত ভগ্নাংশ শাখায়, গুরুত্বপূর্ণ অবদান রেখেছেন। তার রেখে যাওয়া নোটবুক বা ডায়েরি হতে পরবর্তীতে আরও অনেক নতুন সমাধান পাওয়া গেছে। ইংরেজ গণিতবিদ জি এইচ হার্ডি রামানুজনকে অয়েলার ও গাউসের সমপর্যায়ের গণিতবিদ মনে করেন।
  অবিভক্ত ভারতের মাদ্রাজের এক গরিব ব্রাহ্মণ পরিবারের সন্তান রামানুজন ১০ বছর বয়সে গণিতের সঙ্গে পরিচিত হন। তাঁকে এস এল লোনি লিখিত ‘’’ত্রিকোণমিতি’’’ পুস্তকটি দেওয়া হয় এবং তখন থেকে তিনি গণিতে সহজাত প্রতিভা প্রদর্শন করেন।
  ১২ বছরের মধ্যে তিনি ওই পুস্তকের বিষয়গুলোতে দক্ষতা অর্জন করেন। এমন কি তিনি নিজে কিছু উপপাদ্য আবিষ্কার করেন এবং স্বতন্ত্রভাবে অয়েলারের এককত্ব পুনরাবিষ্কার করেন। বিদ্যালয়ে অধ্যয়নকালে তিনি গণিতে বিশেষ দক্ষতা দেখিয়ে পুরস্কার ও প্রশংসা লাভ করেন। ১৭ বছর বয়সে রামানুজন বার্নোলির সংখ্যা ও অয়েলার-মাসেরনি ধ্রুবকের ওপর নিজের গবেষণা সম্পন্ন করেন। কুম্বাকোটম সরকারি কলেজে পড়ার জন্য বৃত্তি পেলেও অ-গাণিতিক বিষয়ে ফেল করার কারণে তার বৃত্তি বাতিল হয়ে যায়। এরপর তিনি অন্য একটি কলেজে নিজের গাণিতিক গবেষণা শুরু করেন। এই সময় জীবন ধারণের জন্য তিনি মাদ্রাজ বন্দর ট্রাস্টের মহা হিসাবরক্ষকের কার্যালয়ে কেরানি পদে যোগ দেন। (সম্পূর্ণ নিবন্ধ...)
• 

  পিথাগোরাসের আবক্ষ মূর্তি কাপিতোলিনে জাদুঘর, রোম

  
  সামোসের পিথাগোরাস (প্রাচীন গ্রিক: Πυθαγόρας ὁ Σάμιος Pythagoras the Samian, অথবা শুধু পিথাগোরাস; ৫২৭– ৪৯৭ খ্রিস্টপূর্বাব্দ ) ছিলেন একজন আয়োনীয় গ্রিক দার্শনিক, গণিতবিদ এবং পিথাগোরাসবাদী ভ্রাতৃত্বের জনক যার প্রকৃতি ধর্মীয় হলেও তা এমন সব নীতির উদ্ভব ঘটিয়েছিল যা পরবর্তীতে প্লেটো এবং এরিস্টটলের মত দার্শনিকদের প্রভাবিত করেছে। তিনি এজিয়ান সাগরের পূর্ব উপকূল অর্থাৎ বর্তমান তুরস্কের কাছাকাছি অবস্থিত সামোস দ্বীপে জন্মেছিলেন। ধারণা করা হয় শৈশবে জ্ঞান অন্বেষণের তাগিদে মিশরসহ বিভিন্ন দেশ ভ্রমণ করেছিলেন। ৫৩০ খ্রিস্টপূর্বাব্দের দিকে ইতালির দক্ষিণাঞ্চলে অবস্থিত গ্রিক কলোনি ক্রোতোনে চলে যান, এবং সেখানে একটি আধ্যাত্মিক ও দার্শনিক ভ্রাতৃত্বমূলক সম্প্রদায় প্রতিষ্ঠা করেন। তার অনুসারীরা তারই নির্ধারিত বিধি-নিষেধ মেনে চলত এবং তার দার্শনিক তত্ত্বসমূহ শিখতো। এই সম্প্রদায় ক্রোতোনের রাজনীতিতে প্রভাব বিস্তার করতে থাকে যা তাদের নিজেদের জন্য বিপজ্জনক হয়ে দাড়ায়। এক সময় তাদের সভাস্থানগুলো পুড়িয়ে দেয়া হয় এবং পিথাগোরাসকে বাধ্য করা হয় ক্রোতোন ছেড়ে যেতে। ধারণা করা হয় জীবনের শেষ দিনগুলো তিনি দক্ষিণ ইতালিরই আরেক স্থান মেতাপোন্তুমে কাটিয়েছিলেন।
  
  পিথাগোরাস কিছু লিখেননি এবং সমসাময়িক কারও রচনাতেও তার সম্পর্কে বিস্তারিত কিছু জানা যায় না। উপরন্তু ১ম খ্রিস্টপূর্বাব্দ থেকে তাকে বেশ অনৈতিহাসিক দৃষ্টিভঙ্গিতে দেখা হতে থাকে। সে সময় ভাবা হতো পিথাগোরাস একজন স্বর্গীয় সত্তা এবং গ্রিক দর্শনে যা কিছু সত্য (এমনকি প্লেটো এবং এরিস্টটলের অনেক পরিণত চিন্তাধারা) তার সবই তিনি শুরু করেছেন। এই ধারণা প্রতিষ্ঠিত করতে এমনকি কিছু গ্রন্থ পিথাগোরাস ও পিথাগোরাসবাদীদের নামে জাল করা হয়েছিল। তাই তার সম্পর্কে সত্যটা জানার জন্য মোটামুটি নির্ভেজাল এবং প্রাচীনতম প্রমাণগুলোর দিকে তাকাতে হবে কারণ স্পষ্টতই পরবর্তীরা তার ব্যাপারে তথ্য বিকৃতি ঘটিয়েছিল। (সম্পূর্ণ নিবন্ধ...)
• 

  

  
  গিয়াসউদিন আবুল‌ ফাতেহ ওমর ইবনে ইব্রাহিম আল-খৈয়াম নিশাপুরি (Ghiyāth ad-Dīn Abu'l-Fatḥ ʿUmar ibn Ibrāhīm al-Khayyām Nīshāpūrī (/ˈoʊmɑːr kaɪˈjɑːm, -ˈjæm, ˈoʊmər/; ফার্সি: ‏غیاث ‌الدین ابوالفتح عمر ابراهیم خیام نیشابورﻯ, উচ্চারণ [xæjˈjɒːm]; জ. মে ১৮ ১০৪৮ - মৃ. ডিসেম্বর ৪, ১১৩১) একজন ইরানের কবি, গণিতবেত্তা, দার্শনিক ও জ্যোতির্বিদ। ইরানের নিশাপুরে জন্মগ্রহণ করার পর যুবা বয়সে তিনি সমরখন্দে চলে যান এবং সেখানে শিক্ষা সমাপ্ত করেন। এর পর বুখারায় নিজেকে মধ্যযুগের একজন প্রধান গণিতবিদ ও জ্যোতির্বিদ হিসাবে প্রতিষ্ঠিত করেন। তার বীজগণিতের গুরুত্বপূর্ণ “Treatise on Demonstration of Problems of Algebra“ গ্রন্থে তিনি ত্রিঘাত সমীকরণ সমাধানের একটি পদ্ধতি বর্ণনা করেন। এই পদ্ধতিতে একটি পরাবৃত্তকে বৃত্তের ছেদক বানিয়ে ত্রিঘাত সমীকরণের সমাধান করা হয়। ইসলামি বর্ষপঞ্জি সংস্কারেও তার অবদান রয়েছে।
  
  তিনি তার কবিতা সমগ্র, যা ওমর খৈয়ামের রূবাইয়াত নামে পরিচিত, তার জন্য বিখ্যাত। কাব্য-প্রতিভার আড়ালে তাঁর গাণিতিক ও দার্শনিক ভূমিকা অনেকখানি ঢাকা পড়েছে। ধারণা করা হয় রনে দেকার্তের আগে তিনি বিশ্লেষণী জ্যামিতি আবিষ্কার করেন। তিনি স্বাধীনভাবে গণিতের দ্বিপদী উপপাদ্য আবিষ্কার করেন। বীজগণিতে ত্রিঘাত সমীকরণের সমাধান তিনিই প্রথম করেন। বহুমুখী প্রতিভার দৃষ্টান্ত দিতে বলা হলে বিশ্বসাহিত্য কিংবা ইতিহাসে যাদের নাম উপেক্ষা করা কঠিন ওমর খৈয়াম তাদের মধ্যে অন্যতম ও শীর্ষস্থানীয়।
  
  দর্শন ও শিক্ষকতায় ওমরের কাজ তার কবিতা ও বৈজ্ঞানিক কাজের আড়ালে অনেকখানি চাপা পড়েছে বলে মনে করা হয়। মধ্যযুগের মুসলিম মনীষা জামাকসারি ওমর খৈয়ামকে “বিশ্ব দার্শনিক” হিসেবে বর্ণনা করেছেন। অনেক সূত্রে জানা গেছে তিনি নিশাপুরে তিন দশক ধরে শিক্ষকতা করেছেন।
  ইরান ও পারস্যের বাইরে ওমরের একটি বড় পরিচয় কবি হিসাবে। এর কারণ তার কবিতা বা রুবাই এর অনুবাদ এবং তার প্রচারের কারণে। ইংরেজি ভাষী দেশগুলোতে এর সবচেয়ে বেশি প্রভাব দেখা যায়। ইংরেজ মনীষী টমাস হাইড প্রথম অ-পারস্য ব্যক্তিত্ব যিনি প্রথম ওমরের কাজ সম্পর্কে গবেষণা করেন। তবে, বহির্বিশ্বে খৈয়ামকে সবচেয়ে বেশি জনপ্রিয় করেন এডওয়ার্ড ফিটজেরাল্ড। তিনি খৈয়ামের ছোট ছোট কবিতা বা রুবাই অনুবাদ করে তা রুবাইয়্যাতে ওমর খৈয়াম নামে প্রকাশ করেন। সুলাইমান নদভী খৈয়াম রচনা করে তার ব্যাপারে বিভিন্ন অভিযোগ জবাব দিয়েছেন। (সম্পূর্ণ নিবন্ধ...)
• 

  ইউক্লিড

  
  ইউক্লিড (জন্ম: অজানা - মৃত্যু: ৩০০ খ্রি. পূ.) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে। এগুলো হলো : ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। পাটিগণিতের মূল নিয়মাবলী, জ্যামিতি, গাণি তিক রাশি ও গাণিতিক সংকেত, সংখ্যাতত্ত্বসহ গণিতের বিভিন্ন শাখায় তার অবদান রয়েছে। অমূলদ রাশির আবিষ্কার গ্রিক গণিতকে যে সংকটে ফেলেছিল তা থেকে উদ্ধার পেতে পাটিগণিত জ্যামিতির দিকে ঝুঁকে পড়েছিল আর ইউক্লিডের গণিতেরও অনেকটাকেই বলা যেতে পারে জ্যামিতিক বীজগণিত। তার প্রধান বৈজ্ঞানিক গ্রন্থ ইউক্লিড’স এলিমেন্টস। এতে আলোচনা আছে তলমিতি ও ঘ্নমিতি এবং সংখ্যাতত্ত্বের বিভিন্ন সমস্যা যেমন অ্যালগরিদম নিয়ে।
  
  ইউক্লিডের জ্যামিতির স্বতঃসিদ্ধ প্রণালী নিম্নোক্ত কয়েকটি মৌলিক প্রতীকির উপর নির্ভরশীল। সেগুলো হচ্ছে : বিন্দু, রেখা, তল, গতি এবং এই দুটি সম্পর্ক_"কোনো বিন্দু একটি তলের অন্তর্গত একটি রেখার উপর অবস্থিত" ও "যে কোনো বিন্দুর অবস্থান অন্য আর দুটি বিন্দুর মধ্যে"। আধুনিক পর্যালোচনা অনুসারে, ইউক্লিডের জ্যামিতির স্বতঃসিদ্ধগুলো এই পাঁচটি ভাগে বিভক্ত : আপত্ন, ক্রম, গতি, সন্ততি এবং সমান্তরাল স্বতঃসিদ্ধ। এই জ্যামিতি অসীম স্তরের উপাদানের কথাও বিবেচনা করেছে। এই প্রসঙ্গে ইউক্লিডিয়ান স্পেস ও ইউক্লিডিয়ান রিং-এর কথা উল্লেখ করা যায়। (সম্পূর্ণ নিবন্ধ...)

গনিত পারেন না বলে কষ্টে থাকবেন না। আমি নিশ্চিত করে বলছি, আমার সমস্যা তার চেয়েও বেশি।

-আলবার্ট আইনস্টাইন

• গণিত বিষয়ক নতুন নিবন্ধ তৈরি অথবা অন্য উইকিপ্রকল্প হতে অনুবাদ করতে পারেন।
• গণিত বিষয়ক টেমপ্লেট- যেমন নিম্নের গণিতের বিষয়বস্তু ও গণিতের ক্ষেত্র হতে লাল লিঙ্ক থাকা বিষয় নিয়ে নিবন্ধ রচনা করতে পারেন।
• বর্তমান নিবন্ধসমূহ তথ্য দিয়ে সমৃদ্ধ, সম্প্রসারণ ও রচনাশৈলীর উন্নয়ন করতে পারেন। নিবন্ধে তথ্যছক না থাকলে প্রাসঙ্গিক তথ্যছক যুক্ত করতে পারেন।
• নিবন্ধগুলিতে উইকিমিডিয়া কমন্স হতে গণিত সংক্রান্ত দরকারী ও প্রাসঙ্গিক মুক্ত চিত্র যুক্ত করতে পারেন।
• গণিত সংক্রান্ত নিবন্ধসমূহে বিষয়শ্রেণী না থাকলে যুক্ত করতে পারেন।
• নিবন্ধসমূহে তথ্যসূত্রের ঘাটতি থাকলে, পর্যাপ্ত সূত্র যোগ করতে পারেন।
• গণিত সম্পর্কিত নিবন্ধসমূহের শেষে {{প্রবেশদ্বার দণ্ড|গণিত}} যুক্ত করতে পারেন।

সাধারণ	ভিত্তি	সংখ্যা তত্ত্ব	বিচ্ছিন্ন গণিত
গণিতবিদ তালিকা গণিতের ইতিহাস গণিতের দর্শন গাণিতিক প্রতীক-চিহ্নাদি গাণিতিক সৌন্দর্য গণিত শিক্ষা গণিতের ক্ষেত্রসমূহ গাণিতিক পরিভাষা	গণিতের ভিত্তি সেট তত্ত্ব প্রাথমিক সেট তত্ত্ব স্বতঃসিদ্ধ সেট তত্ত্ব গাণিতিক যুক্তিবিজ্ঞান প্রমাণ তত্ত্ব মডেল তত্ত্ব ক্যাটেগরি তত্ত্ব টপোস তত্ত্ব গ্যোডেলের অসম্পূর্ণতা উপপাদ্য	সংখ্যাতত্ত্ব বীজগাণিতিক সংখ্যাতত্ত্ব বিশ্লেষণী সংখ্যাতত্ত্ব পাটীগণিত সংখ্যা স্বাভাবিক সংখ্যা মৌলিক সংখ্যা মূলদ সংখ্যা বীজগাণিতিক সংখ্যা পাটীগণিতের মৌলিক উপপাদ্য	বিচ্ছিন্ন গণিত গুচ্ছ-বিন্যাস তত্ত্ব গ্রাফ তত্ত্ব টপোগাণিতিক গ্রাফ তত্ত্ব চার বর্ণ উপপাদ্য গেম তত্ত্ব বিচ্ছিন্ন জ্যামিতি তাত্ত্বিক কম্পিউটার বিজ্ঞান গণনীয়তা তত্ত্ব গণনামূলক জটিলতা তত্ত্ব তথ্য তত্ত্ব
বিশ্লেষণ গণিত	বীজগণিত	জ্যামিতি ও টপোগণিত	ব্যবহারিক গণিত
বিশ্লেষণ বাস্তব বিশ্লেষণ জটিল বিশ্লেষণ ফাংশনভিত্তিক বিশ্লেষণ ভাজিত বিশ্লেষণ ক্যালকুলাস ভেক্টর ক্যালকুলাস অন্তরক সমীকরণ ভেদ ক্যালকুলাস ক্যালকুলাসের মৌলিক উপপাদ্য পরিমাপ তত্ত্ব বিশেষ ফাংশনসমূহ ত্রিকোণমিতি	বীজগণিত প্রাথমিক বীজগণিত বিমূর্ত বীজগণিত ল্যাটিস গ্রুপ, গ্রুপ তত্ত্ব রিং তত্ত্ব ফিল্ড, ফিল্ড তত্ত্ব বিনিময় বীজগণিত রৈখিক বীজগণিত ভেক্টর জগৎ মেট্রিক্স, মেট্রিক্স তত্ত্ব রৈখিক রূপান্তর, রৈখিক অপারেটর ও রৈখিক ফাংশনাল বহুরৈখিক বীজগণিত টেনসর বীজগণিত ক্যাটেগরি তত্ত্ব হোমোলজিকাল বীজগণিত বিশ্বজনীন বীজগণিত শৃঙ্খলা তত্ত্ব বীজগণিতের মৌলিক উপপাদ্য	জ্যামিতি ইউক্লিডীয় জ্যামিতি পিথাগোরাসের উপপাদ্য অ-ইউক্লিডীয় জ্যামিতি (অধিবৃত্তিক, উপবৃত্তিক) পরম জ্যামিতি অ্যাফাইন জ্যামিতি অভিক্ষেপ জ্যামিতি অন্তরক জ্যামিতি রিমানীয় জ্যামিতি লী গ্রুপ বীজগাণিতিক জ্যামিতি টপোগণিত সাধারণ টপোগণিত বীজগাণিতিক টপোগণিত জ্যামিতিক টপোগণিত	ব্যবহারিক গণিত সাংখ্যিক বিশ্লেষণ গাণিতিক জীববিজ্ঞান সেরা-অনুকূলকরণ গতিশীল ব্যবস্থা বিশৃঙ্খলা তত্ত্ব আর্থিক গণিত ক্রিপ্টোগ্রাফি গাণিতিক পদার্থবিজ্ঞান চিরায়ত বলবিজ্ঞান সম্ভাবনা পরিসংখ্যান অপারেশন গবেষণা

বীজগণিত • বিশ্লেষণ • ফলিত গণিত • ক্যালকুলাস • ক্যাটেগরি তত্ত্ব • বিশৃঙ্খলা তত্ত্ব • গুচ্ছ-বিন্যাস তত্ত্ব • ক্রীড়া তত্ত্ব • জ্যামিতি • গ্রাফ তত্ত্ব • গ্রুপ তত্ত্ব • রৈখিক বীজগণিত • যুক্তিবিজ্ঞান • সংখ্যাতত্ত্ব • সাংখ্যিক বিশ্লেষণ • সর্বোন্নতিকরণ • শৃঙ্খলা তত্ত্ব • সম্ভাবনা ও পরিসংখ্যান • সেট তত্ত্ব • পরিসংখ্যান • টপোগণিত • ত্রিকোণমিতি

---

গণিতবিদ • গণিতের ইতিহাস • গণিতের পুরস্কার • গণিত শিক্ষা • গণিতভিত্তিক প্রতিষ্ঠান ও সম্প্রদায় • গণিত বিষয়ক রচনা • গাণিতিক অঙ্কপাতন • গাণিতিক উপপাদ্য • প্রমাণ • গণিতের অসমাধানকৃত সমস্যাসমূহ

---

বিষয়শ্রেণী ধাঁধা

নিচের বিষয়শ্রেণীগুলোর অধীনে সবগুলো নিবন্ধ সাজানো আছে। [►] চিহ্নে ক্লিক করলেই উপ-বিষয়শ্রেণী দেখতে পাবেন।

গণিত

গণিতবিদ

গণিতের ক্ষেত্র

গণিত সম্পর্কিত তালিকা

গণিত বিষয়ক সৃষ্টিকর্ম

গাণিতিক অঙ্কপাতন

গণিতের ইতিহাস

গাণিতিক উপপাদ্য

গণিত বিষয়াবলী

গণিতের দর্শন

গাণিতিক ধারণা

গাণিতিক ধ্রুবক

গাণিতিক পরিভাষা

গাণিতিক বিজ্ঞান পেশা

গাণিতিক প্রমাণ

গণিত ও সংস্কৃতি

গাণিতিক সরঞ্জাম

প্রবেশদ্বার

কার্যকলাপ সংস্কৃতি ভূগোল স্বাস্থ্য ইতিহাস গণিত প্রকৃতি জাতি দর্শন ধর্ম সমাজ প্রযুক্তি অজানা প্রবেশদ্বার

• প্রবেশদ্বার কী?
• প্রবেশদ্বারসমূহের তালিকা
• নির্বাচিত প্রবেশদ্বার