与非门

NAND 逻辑门
输入		输出
A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

与非门（英語：NAND gate）是数字逻辑中实现逻辑与非的逻辑门。若输入均为高电平（1），则输出为低电平（0）；若输入中至少有一个为低电平（0），则输出为高电平（1）。与非门是一种通用的逻辑门，因为任何布尔函数都能用与非门实现。

使用特定逻辑电路的数字系统利用了与非门的函数完备性（功能完备性）。复杂的逻辑表达式常以其他逻辑函数表示，如与、或、非，而将表达式改写为用逻辑与非表示的式子可以节约成本，因为使用与非门实现电路能使电路结构更为紧凑。

与非门并不仅限於2输入，可以是多输入，这时当输入全为高电平时，输出为低电平；若有任意一个输入为低电平，则输出为高电平。这些门电路不再是简单的二进制运算器，而是可作为n元运算器使用的门电路。代数中，这些门电路可以用函数NAND(a, b, ..., n)表示，等价於NOT(a AND b AND ... AND n)。

概述

输入 A B		输出 A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

下列包括逻辑门的3种符号：形状特征型符号（ANSI/IEEE Std 91-1984）、IEC矩形国标符号（IEC 60617-12）和不再使用的DIN符号（DIN 40700）。其他的逻辑门符号见逻辑门符号表。

表达式

符号

功能表

继电器逻辑

ANSI/IEEE Std 91-1984

IEC 60617-12

DIN 40700

Y={\overline {A\,B}}

Y={\overline {A\cdot B}}

Y=A{\overline {\wedge }}B

Y={\overline {A\wedge B}}

A	B	$Y={\overline {A\,B}}$
0	0	1
0	1	1
1	0	1
1	1	0

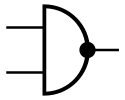硬件描述和引脚分配

与非门是基本的门电路，因此常用於晶体管－晶体管逻辑（TTL）和CMOS 集成电路。

TTL版本

反及閘是TTL中最基本、電路最簡單的多輸入邏輯閘，在TTL電路中扮演重要角色。 7400內含四組2輸入反及閘，是TTL編號中排在第一的型號。

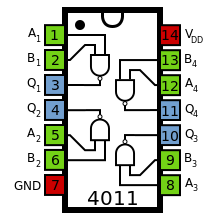
CMOS版本

标准4000系列 CMOS 集成电路为4011，包含4个独立的2端输入与非门。

可用型号

大多数半导体制造商都生产这种元件，如飞兆半导体公司、飞利浦、德州仪器，封装方式分为雙列直插封裝和SOIC封装（英语：small-outline integrated circuit）两种。元件的数据表可在大多数元件数据库查询到。

下列是可以获得的标准2、3、4、8输入与非门型号：

CMOS
- 4011：四2输入与非门
- 4023：三3输入与非门
- 4012：双4输入与非门
- 4068：单8输入与非门
TTL
- 7400：四2输入与非门
- 7410：三3输入与非门
- 7420：双4输入与非门
- 7430：单8输入与非门

实现

与非门具有函数完备性，因此其他的逻辑功能（与、非等）都可以仅用与非门来实现。一个完整的处理器可以只用与非门制作出来。在使用多发射极晶体管的TTL集成电路中，与非门需要的晶体管也少於其他任何门电路。

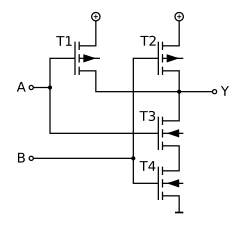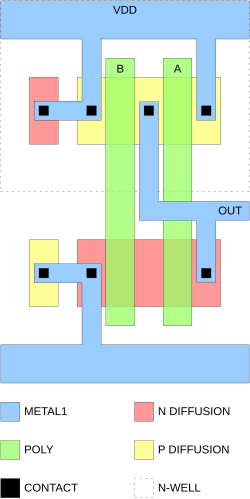应用

与非门是数字电子技术中最重要的逻辑门，可组成加法器、数据选择器等组合逻辑电路，而且由於其完备性，可以仅用其组成电路，有利於电路的集成，能使集成电路的造价降低很多。

与非逻辑

与非逻辑实现的其他逻辑运算：
运算	实现
NOT x	x NAND x
x AND y	(x NAND y) NAND (x NAND y)
x NAND y	x NAND y
x OR y	(x NAND x) NAND (y NAND y)
x NOR y	((x NAND x) NAND (y NAND y)) NAND ((x NAND x) NAND (y NAND y))
x XOR y	(x NAND (y NAND y)) NAND ((x NAND x) NAND y)
x XOR y	((x NAND y) NAND y)) NAND ((x NAND y) NAND x))
x XNOR y	(x NAND y) NAND ((x NAND x) NAND (y NAND y))
x XNOR y	≡ x ⇔ y
x ⇒ y	x NAND (y NAND y)
x ⇐ y	(x NAND x) NAND y
x ⇔ y	(x NAND y) NAND ((x NAND x) NAND (y NAND y))
x ⇔ y	≡ x XNOR y
重言式	(x NAND x) NAND x
矛盾式	((x NAND x) NAND x) NAND ((x NAND x) NAND x)

参见

外部链接

（英文）http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/nand.html （页面存档备份，存于互联网档案馆）

查论编数字电路
数字电路概要	数字系统
概念	数字信号布尔代数開關组合逻辑电路时序逻辑电路同步異步真值表卡诺图有限状态机米利机摩尔机
硬件模块	邏輯閘与或非同与非或非异或同或蘊含 TTL 74190 CMOS 加法器乘法器编码器译码器数据选择器锁存器寄存器触发器 RS D JK T 儲存裝置 ROM RAM 類比數位轉換器數位類比轉換器
IC、VLSI	定制程度（半、全） PLD PAL PLA GAL CPLD FPGA ASIC 设计验证电子设计自动化（EDA）硬件描述语言 Verilog VHDL Chisel (programming language)（英语：Chisel (programming language)）硬件验证语言逻辑综合 SystemVerilog

查论编逻辑联结词
恆真（ $\top$ ）
与非（ $\uparrow$ ）反蕴涵（ $\leftarrow$ ）蕴涵（ $\rightarrow$ ）或（ $\lor$ ）
非（ $\neg$ ）异或（ $\oplus$ ）双条件（ $\leftrightarrow$ ）命题
或非（ $\downarrow$ ）非蕴涵（ $\nrightarrow$ ）反非蕴涵（ $\nleftarrow$ ）与（ $\land$ ）
恆假（ $\bot$ ）