梯度下降法

梯度下降法（英語：Gradient descent）是一种求解无约束最优化问题的一阶迭代最优化算法，它被用来求得可微函数的局部极小值，通常也称为最陡下降法，但是不該與近似積分的最陡下降法（英語：Method of steepest descent）混淆。 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索，因为这是最陡下降的方向。如果相反地向梯度正方向迭代进行搜索，则会接近函数的局部极大值点，这个过程则被称为梯度上升法。梯度下降法在机器学习中对于成本的最小化或损失函数的最小化都特别有用。梯度下降法不应与局部搜索算法（英語：local search algorithms）相混淆，尽管两者都是迭代最优化算法。

梯度下降法通常被认为是奧古斯丁-路易·柯西（法語：Augustin-Louis Cauchy）在1847年首次提出的。雅克·所罗门·阿达马（法語：Jacques Solomon Hadamard）在1907年独立提出了一个类似的方法。哈斯凯尔·柯里（英語：Haskell Brooks Curry）在1944年首先研究了该方法对非线性优化问题的收敛性；在随后的几十年里，该方法得到了越来越多的研究和使用。

随机梯度下降法（英語：stochastic gradient descent）作为梯度下降法的一个简单延展，是目前用于训练大多数深度学习结构（英語：deep networks）的最基本的算法。

描述

梯度下降法的描述。

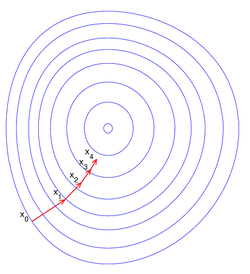
梯度下降方法基于以下的观察：如果实值函数$F(\mathbf {x} )$在点$\mathbf {a}$处可微且有定义，那么函数$F(\mathbf {x} )$在$\mathbf {a}$点沿着梯度相反的方向 $-\nabla F(\mathbf {a} )$ 下降最多。

因而，如果

$\mathbf {b} =\mathbf {a} -\gamma \nabla F(\mathbf {a} )$

对于一個足够小数值$\gamma >0$時成立，那么$F(\mathbf {a} )\geq F(\mathbf {b} )$。

考虑到这一点，我们可以从函数$F$的局部极小值的初始估计$\mathbf {x} _{0}$出发，并考虑如下序列 $\mathbf {x} _{0},\mathbf {x} _{1},\mathbf {x} _{2},\dots$使得

$\mathbf {x} _{n+1}=\mathbf {x} _{n}-\gamma _{n}\nabla F(\mathbf {x} _{n}),\ n\geq 0$。

因此可得到

$F(\mathbf {x} _{0})\geq F(\mathbf {x} _{1})\geq F(\mathbf {x} _{2})\geq \cdots ,$

如果顺利的话序列$(\mathbf {x} _{n})$收敛到期望的局部极小值。注意每次迭代步长$\gamma$可以改变。

右侧的图片示例了这一过程，这里假设$F$定义在平面上，并且函数图像是一个碗形。蓝色的曲线是等高线（水平集），即函数$F$为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线垂直）。沿着梯度下降方向，将最终到达碗底，即函数$F$局部極小值的点。

例子

梯度下降法处理一些复杂的非线性函数会出现问题，例如Rosenbrock函數

$f(x,y)=(1-x)^{2}+100(y-x^{2})^{2}.\quad$

其最小值在$(x,y)=(1,1)$处，数值为$f(x,y)=0$。但是此函数具有狭窄弯曲的山谷，最小值$(x,y)=(1,1)$就在这些山谷之中，并且谷底很平。优化过程是之字形的向极小值点靠近，速度非常缓慢。

下面这个例子也鲜明的示例了"之字"的上升（非下降），这个例子用梯度上升（非梯度下降）法求$F(x,y)=\sin \left({\frac {1}{2}}x^{2}-{\frac {1}{4}}y^{2}+3\right)\cos(2x+1-e^{y})$的局部极大值（非局部极小值）。

|}

缺点

梯度下降法的缺點包括：

• 靠近局部極小值时速度减慢。
• 直線搜索可能會產生一些問題。
• 可能會“之字型”地下降。

上述例子也已体现出了这些缺点。

参阅

• 共轭梯度法
• 随机梯度下降法
• 最优化

• 线搜索
• 反向傳播算法
• 量子退火

参考文献

• Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
• Jan A. Snyman (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Publishing. ISBN 0-387-24348-8

外部链接

• （英文）Interactive examples of gradient descent and some step size selection methods （页面存档备份，存于互联网档案馆）
• （英文）Using gradient descent in C++, Boost, Ublas for linear regression （页面存档备份，存于互联网档案馆）