模版 (數值分析)
外观
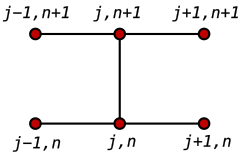
在數學的偏微分方程數值方法裡,模版(stencil)是有關幾何安排的資訊,會用在一個點周圍點上的資訊來求得所關注點的資訊。模版是許多求解偏微分方程(PDE)數值方法演算法的基礎。五點模版和克兰克-尼科尔森方法模版就是模版的例子。
模版可分為兩類:緊緻模版和非緊緻模版,兩者的差異在只利用關注點鄰近的點,或是會用到更遠處的點。
在一維模版中,會用n-1、n和n+1表示時間的步階,其中n和n-1是數值已知的,而有限體積空間上的分佈會表示為j-1、j和j+1。
名稱
[编辑]在偏微分方程研究的早期,就已有用圖示表示所使用節點和係數的作法,當時的名稱有relaxation patterns、operating instructions、lozenges或point patterns等[1][2]。後來將此名稱取名為"模版"(stencil),是將模板噴畫中模板的概念用在數值方法求解時,用圖示表示在特定一步需要其他哪些點的資訊[2]。
係數計算
[编辑]偏微分方程數值方法中,確定方法和模版後,其有限差分係數就固定了,此係數可用拉格朗日多項式在這些點之間內插,再微分求得[3],作法是計算附近每個點的泰勒级数,再求解方程式[4],或是強制該模式就符合最多到模版階數的單項式[3]。
相關條目
[编辑]參考資料
[编辑]- ^ Emmons, Howard W. The numerical solution of partial differential equations (PDF). Quarterly of Applied Mathematics. 1 October 1944, 2 (3): 173–195 [17 April 2017]. doi:10.1090/qam/10680
 .
.
- ^ 2.0 2.1 Milne, William Edmund. Numerical solution of differential equations. 1st. Wiley. 1953: 128–131. OCLC 527661 (English).
- ^ 3.0 3.1 Fornberg, Bengt; Flyer, Natasha. Brief Summary of Finite Difference Methods. A Primer on Radial Basis Functions with Applications to the Geosciences. Society for Industrial and Applied Mathematics. 2015 [9 April 2017]. ISBN 9781611974027. doi:10.1137/1.9781611974041.ch1.
- ^ Taylor, Cameron. Finite Difference Coefficients Calculator. web.media.mit.edu. [9 April 2017] (英语).
- W. F. Spotz. High-Order Compact Finite Difference Schemes for Computational Mechanics. PhD thesis, University of Texas at Austin, Austin, TX, 1995.
- Communications in Numerical Methods in Engineering, Copyright © 2008 John Wiley & Sons, Ltd.
