등비급수

수학에서 등비급수 또는 기하급수(Geometric series)는 등비수열의 항들을 합한 급수이며, 이 급수에서 연속적인 항들의 비는 일정하다. 예를 들어, 급수 ${\tfrac {1}{2}}+{\tfrac {1}{4}}+{\tfrac {1}{8}}+\cdots$는 공비 ${\tfrac {1}{2}}$를 갖는 등비급수이며, 합 $1$로 수렴한다. 등비급수의 각 항은 앞 항과 뒤 항의 기하 평균이며, 이는 산술급수의 각 항이 이웃 항들의 산술 평균인 방식과 같다.

기원전 5세기의 그리스 철학자인 엘레아의 제논의 시간과 운동에 관한 제논의 역설은 등비급수를 포함하는 것으로 해석되어 왔지만, 이러한 급수는 한두 세기 후 그리스 수학자들에 의해 공식적으로 연구되고 적용되었다. 예를 들어, 아르키메데스는 기원전 3세기에 포물선 안의 넓이를 계산하는 데 이를 사용했다. 오늘날 등비급수는 수리금융학, 프랙탈의 넓이 계산, 다양한 컴퓨터 과학 분야에서 사용된다.

등비급수는 일반적으로 실수나 복소수를 다루지만, 행렬 값 등비급수, 함수 값 등비급수, $p$-진수 등비급수, 그리고 가장 일반적으로 추상대수학의 체, 환, 반환의 원소로 구성된 등비급수에 대한 중요한 결과와 응용도 있다.

정의 및 예시

등비급수는 등비수열이라는 특별한 유형의 수열에서 파생된 무한급수이다. 이는 등비수열의 무한히 많은 항을 합한 것으로, 초기 항 $a$에서 시작하여 다음 항은 초기 항에 공비 $r$로 알려진 상수 값을 곱한 값이다. 각 항에 공비를 연속적으로 곱함으로써, 등비급수는 수학적으로 다음과 같이 정의될 수 있다. $$a+ar+ar^{2}+ar^{3}+\cdots =\sum _{k=0}^{\infty }ar^{k}.$$ 무한 등비급수의 유한 초기 부분의 합을 유한 등비급수라고 하며, 다음과 같이 표현된다. $$a+ar+ar^{2}+ar^{3}+\cdots +ar^{n}=\sum _{k=0}^{n}ar^{k}.$$

$r>1$일 때는 종종 성장률 또는 확장률이라고 불린다. $0<r<1$일 때는 종종 감소율 또는 축소율이라고 불리는데, 이는 $k$를 일종의 이산 시간 변수로 해석하여 "율"이라는 개념이 나온다. 응용 분야에서 특정 유형의 성장, 확장, 축소 및 감소에 대한 전문 용어가 있을 때, 해당 용어는 등비급수의 $r$ 매개변수를 명명하는 데도 종종 사용된다. 예를 들어, 경제학에서는 물가 수준의 증가 및 감소율을 인플레이션율 및 디플레이션율이라고 부르는 반면, 투자의 가치 증가율에는 수익률과 이자율이 포함된다.

보라색 사각형의 넓이로 나타낸 등비급수 ${\textstyle {\frac {1}{4}}+{\frac {1}{16}}+{\frac {1}{64}}+{\frac {1}{256}}+\cdots }$. 각 보라색 사각형은 다음 큰 사각형 넓이의 ⁠1/4⁠을 차지한다. ${\textstyle {\frac {1}{2}}\times {\frac {1}{2}}={\frac {1}{4}}}$, ${\textstyle {\frac {1}{4}}\times {\frac {1}{4}}={\frac {1}{16}}}$ 등등. 따라서 보라색 사각형들의 넓이의 합은 큰 사각형 넓이의 3분의 1이다.

무한히 많은 항을 합할 때, 등비급수는 수렴할 수도 있고 발산할 수도 있다. 수렴은 무한히 많은 항을 합한 후에 값이 존재한다는 것을 의미하고, 발산은 합한 후에 값이 존재하지 않는다는 것을 의미한다. 등비급수의 수렴은 공비의 값에 따라 설명될 수 있으며, § Convergence of the series and its proof를 참조하라. 그란디의 급수는 $1-1+1-1+\cdots$로 표현될 수 있는 발산 급수의 예로, 초기 항은 $1$이고 공비는 $-1$이다. 이는 이 급수가 세 가지 다른 값을 가지기 때문이다.

영원히 반복되는 패턴을 가진 십진법 소수는 등비급수로 해석될 수 있으며, 이를 통해 두 정수의 비로 표현될 수 있다. 예를 들어, 순환소수 $0.7777\ldots$는 다음과 같이 등비급수로 쓸 수 있다. $$0.7777\ldots ={\frac {7}{10}}+{\frac {7}{10}}\left({\frac {1}{10}}\right)+{\frac {7}{10}}\left({\frac {1}{10^{2}}}\right)+{\frac {7}{10}}\left({\frac {1}{10^{3}}}\right)+\cdots ,$$ 여기서 초기 항은 $a={\tfrac {7}{10}}$이고 공비는 $r={\tfrac {1}{10}}$이다.

급수의 수렴과 그 증명

무한 등비급수의 부분합의 무한 수열의 수렴은 공비 $r$의 크기에만 의존한다.

• $\vert r\vert <1$일 경우, 급수의 항들은 0에 가까워지고(크기가 점점 작아짐) 부분합 $S_{n}$의 수열은 ${\textstyle {\frac {a}{1-r}}}$의 극한값으로 수렴한다.
• $\vert r\vert >1$일 경우, 급수의 항들은 크기가 점점 커지고 항들의 부분합도 크기가 점점 커지므로 급수는 발산한다.
• $\vert r\vert =1$일 경우, 급수의 항들은 크기가 더 커지거나 작아지지 않고 급수의 부분합 수열은 수렴하지 않는다. $r=1$일 경우, 급수의 모든 항이 같고 $|S_{n}|$은 무한대로 증가한다. $r=-1$일 경우, 항들은 $a$와 $-a$의 두 값을 번갈아 가지므로 항들의 부분합 수열은 $a$와 0의 두 값 사이에서 진동한다. 그란디의 급수에서 한 가지 예를 찾을 수 있다. $r=i$이고 $a=1$일 경우, 부분합은 $1,1+i,i,0,1,1+i,i,0,\ldots$ 값들 사이에서 주기적으로 순환하며 극한으로 수렴하지 않는다. 일반적으로 $$r=e^{\frac {2\pi i}{\tau }}$$ (모든 정수 $\tau$에 대해)이고 $a\neq 0$일 경우, 급수의 부분합은 $\tau$의 주기로 무기한 순환하며 극한으로 수렴하지 않는다.

수렴 속도는 수열이 그 극한에 얼마나 빨리 접근하는지 보여준다. 등비급수의 경우—관련 수열은 $S_{n}$이고 그 극한은 $S$이다—속도와 차수는 다음을 통해 찾는다. $$\lim _{n\rightarrow \infty }{\frac {\left|S_{n+1}-S\right|}{\left|S_{n}-S\right|^{q}}},$$ 여기서 $q$는 수렴 차수를 나타낸다. ${\textstyle |S_{n}-S|=\left|{\frac {ar^{n+1}}{1-r}}\right|}$를 사용하고 수렴 차수 $q=1$을 선택하면 다음과 같다. $$\lim _{n\rightarrow \infty }{\frac {\left|{\frac {ar^{n+2}}{1-r}}\right|}{\left|{\frac {ar^{n+1}}{1-r}}\right|^{1}}}=|r|.$$ 급수가 수렴할 때, $|r|$이 $1$에 가까워질수록 수렴 속도는 느려진다. 수렴 패턴은 공비의 부호 또는 복소수 편각에 따라 달라지기도 한다. 만약 $r>0$이고 $|r|<1$이면 모든 항이 같은 부호를 가지며 항의 부분합은 최종 극한에 단조롭게 접근한다. 만약 $r<0$이고 $|r|<1$이면 등비급수의 인접 항들이 양수와 음수 사이에서 번갈아 나타나고, 항의 부분합 $S_{n}$은 최종 극한 $S$의 위아래로 진동한다. 복소수 $r$과 $|r|<1$인 경우, $S_{n}$은 나선형 패턴으로 수렴한다.

수렴은 다음과 같이 증명된다. 등비급수의 첫 $n+1$개 항의 부분합은 $r^{n}$ 항까지 포함하여 다음과 같다. $$S_{n}=ar^{0}+ar^{1}+\cdots +ar^{n}=\sum _{k=0}^{n}ar^{k},$$ 닫힌 형태는 다음과 같다. $$S_{n}={\begin{cases}a(n+1)&r=1\\a\left({\frac {1-r^{n+1}}{1-r}}\right)&{\text{otherwise}}\end{cases}}$$ 여기서 $r$는 공비이다. $r=1$인 경우는 단순히 덧셈의 경우로, 산술급수의 경우이다. $r\neq 1$인 경우의 부분합 $S_{n}$의 공식은 다음과 같이 유도될 수 있다. $${\begin{aligned}S_{n}&=ar^{0}+ar^{1}+\cdots +ar^{n},\\rS_{n}&=ar^{1}+ar^{2}+\cdots +ar^{n+1},\\S_{n}-rS_{n}&=ar^{0}-ar^{n+1},\\S_{n}\left(1-r\right)&=a\left(1-r^{n+1}\right),\\S_{n}&=a\left({\frac {1-r^{n+1}}{1-r}}\right),\end{aligned}}$$ $r\neq 1$인 경우이다. $r$이 1에 접근할 때, 다항식 나눗셈 또는 로피탈의 정리를 통해 $S_{n}=a(n+1)$인 경우를 얻는다.

등비급수의 합 공식에 대한 그림 없이 증명 (만약 $|r|<1$이고 $n\to \infty$이면 $r^{n}$ 항은 사라지면서 ${\textstyle \lim _{n\to \infty }S_{n}={\frac {a}{1-r}}}$만 남는다.) 이 그림은 본문과는 약간 다른 $S_{n}$의 정의를 사용하며, 한 항만큼 이동되어 있다.

$n$이 무한대로 접근할 때, 이 부분합 수열이 극한으로 수렴하려면 r의 절댓값이 1보다 작아야 한다. 그럴 때 급수는 절대 수렴한다. 무한 급수는 다음과 같이 된다. $${\begin{aligned}S&=a+ar+ar^{2}+ar^{3}+ar^{4}+\cdots \\&=\lim _{n\rightarrow \infty }S_{n}\\&=\lim _{n\rightarrow \infty }{\frac {a(1-r^{n+1})}{1-r}}\\&={\frac {a}{1-r}}-{\frac {a}{1-r}}\lim _{n\rightarrow \infty }r^{n+1}\\&={\frac {a}{1-r}},\end{aligned}}$$ $|r|<1$일 때이다.

이 수렴 결과는 다른 급수의 수렴을 증명하는 데도 널리 적용된다. 그러한 급수의 항들이 적절한 등비급수로 위에서 제한될 수 있을 때 그렇다. 이 증명 전략은 무한급수의 수렴을 위한 비 판정법과 근 판정법의 기초이다.

멱급수와의 관계

등비급수처럼 멱급수도 등비급수의 $r$에 해당하는 연속적인 거듭제곱으로 올려진 공통 변수에 대한 하나의 매개변수를 갖지만, 각 항에 대한 추가 매개변수 $a_{0},a_{1},a_{2},\ldots ,$를 가지며, 등비급수의 각 항에 있는 $r^{k}$의 공통 계수인 단일 추가 매개변수 $a$ 대신 각 $x^{0},x^{1},x^{2},\ldots$의 개별 계수에 대해 하나씩 갖는다. 따라서 등비급수는 모든 $k$에 대해 $a_{k}=a$이고 $x=r$인 계수 수열을 만족하는 멱급수의 한 종류로 간주될 수 있다.

이러한 특별한 멱급수 클래스는 조합론에서 생성 함수 연구나 해석학에서 발산 급수의 합과 같이 수학에서 중요한 역할을 한다. 다른 많은 멱급수는 등비급수의 변형 및 조합으로 작성될 수 있으므로, 등비급수 공식은 해당 멱급수의 공식도 계산하는 데 편리한 도구가 된다.

멱급수로서 등비급수는 수렴 반경이 1이다. 이것은 코시-아다마르 정리와 모든 $a$에 대해 $$\lim _{n\rightarrow \infty }{\sqrt[{n}]{a}}=1$$이라는 사실의 결과로 볼 수 있거나, 무한급수의 수렴에 대한 비 판정법의 결과로 볼 수 있다. $$\lim _{n\rightarrow \infty }{\frac {|ar^{n+1}|}{|ar^{n}|}}=|r|$$는 $|r|<1$일 때만 수렴을 의미한다. 그러나 비 판정법과 코시-아다마르 정리 모두 등비급수 공식을 논리적으로 선행하는 결과로 사용하여 증명되므로, 이러한 추론은 미묘하게 순환적일 수 있다.

배경

2,500년 전, 그리스 수학자들은 양수의 무한히 긴 목록이 무한대에 합산되어야 한다고 믿었다. 따라서 엘레아의 제논은 다음과 같이 증명하는 역설을 만들었다. 한 장소에서 다른 장소로 걷기 위해서는 먼저 그 거리의 절반을 걸어야 하고, 그 다음 남은 거리의 절반을, 그리고 그 남은 거리의 절반을 걸어야 하며, 도착하기 전에 무한히 많은 구간을 통과해야 한다. 그렇게 함으로써 그는 고정된 거리를 무한히 긴 반으로 줄인 남은 거리의 목록으로 나누었고, 각 거리는 0보다 큰 길이를 가졌다. 제논의 역설은 그리스인들에게 양수의 무한히 긴 목록이 무한대로 합산되어야 한다는 가정이 잘못되었음을 드러냈다.

유클리드의 원론, 제9권, 명제 35. "어떠한 다수의 연속적으로 비례하는 수가 있고, 둘째 항에서 첫째 항을 빼고 마지막 항에서도 빼면, 둘째 항에서 첫째 항을 뺀 초과분과 같이 마지막 항의 초과분은 그 앞의 모든 항들의 합에 비례한다."

아르키메데스의 포물선 부분 무한 분할

유클리드의 원론은 세계에서 가장 오래된 연속적으로 사용되는 수학 교과서라는 명예를 지니며, 제9권 명제 35에서 유한 등비급수의 합에 대한 증명을 포함하고 있으며, 인접한 그림에 설명되어 있다.

아르키메데스는 그의 포물선 구적법에서 등비급수의 합을 사용하여 포물선과 직선으로 둘러싸인 영역의 넓이를 계산했다. 아르키메데스의 정리는 포물선 아래의 총 넓이가 파란색 삼각형 넓이의 ⁠4/3⁠임을 나타낸다. 그의 방법은 인접한 그림에 보이는 것처럼 영역을 무한한 삼각형으로 분할하는 것이었다. 그는 각 녹색 삼각형이 파란색 삼각형 넓이의 ⁠1/8⁠을 차지하고, 각 노란색 삼각형은 녹색 삼각형 넓이의 ⁠1/8⁠을 차지하는 식으로 진행된다는 것을 알아냈다. 파란색 삼각형의 넓이를 1로 가정하면, 총 넓이는 무한 급수의 합이 된다. $$1+2\left({\frac {1}{8}}\right)+4\left({\frac {1}{8}}\right)^{2}+8\left({\frac {1}{8}}\right)^{3}+\cdots .$$ 여기서 첫 번째 항은 파란색 삼각형의 넓이를 나타내고, 두 번째 항은 두 개의 녹색 삼각형의 넓이이며, 세 번째 항은 네 개의 노란색 삼각형의 넓이이고, 그 다음은 계속 이어진다. 분수를 단순화하면 다음과 같다. $$1+{\frac {1}{4}}+{\frac {1}{16}}+{\frac {1}{64}}+\cdots ,$$ 이는 공비 $r={\tfrac {1}{4}}$를 갖는 등비급수이며, 그 합은 다음과 같다.

${\frac {1}{1-r}}\ ={\frac {1}{1-{\frac {1}{4}}}}={\frac {4}{3}}.$

니콜라 오렘이 무한급수 ${\tfrac {1}{2}}+{\tfrac {2}{4}}+{\tfrac {3}{8}}+{\tfrac {4}{16}}+{\tfrac {5}{32}}+{\tfrac {6}{64}}+{\tfrac {7}{128}}+\cdots$가 2로 수렴함을 결정하는 데 사용한 2차원 등비급수 다이어그램.

니콜라스 오렘은 조화급수의 발산에 대한 우아하고 간결한 증명 외에도, 가브리엘의 계단으로 알려진 산술-기하 수열이 $${\frac {1}{2}}+{\frac {2}{4}}+{\frac {3}{8}}+{\frac {4}{16}}+{\frac {5}{32}}+{\frac {6}{64}}+{\frac {7}{128}}+\cdots =2.$$ 그의 기하학적 증명 다이어그램(인접 다이어그램과 유사)은 2차원 등비급수를 보여준다. 첫 번째 차원은 수평으로, 맨 아래 행에 초기 값 $a={\tfrac {1}{2}}$와 공비 $r={\tfrac {1}{2}}$를 갖는 등비급수를 나타낸다. $$S={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+{\frac {1}{32}}+\cdots ={\frac {\frac {1}{2}}{1-{\frac {1}{2}}}}=1.$$ 두 번째 차원은 수직으로, 맨 아래 행이 새로운 초기 항 $a=S$이고 그 위로 각 후속 행이 같은 공비 $r={\tfrac {1}{2}}$에 따라 줄어들어 합이 $T$인 또 다른 등비급수를 만든다. $${\begin{aligned}T&=S\left(1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\cdots \right)\\&={\frac {S}{1-r}}={\frac {1}{1-{\frac {1}{2}}}}=2.\end{aligned}}$$ 이 접근 방식은 고차원에도 유용하게 일반화되며, 그 일반화는 아래 § Connection to the power series에서 설명되어 있다.

응용

위에서 언급했듯이, 등비급수는 경제학 분야에 적용될 수 있다. 이는 등비급수의 공비가 물가 수준의 증가율과 감소율을 나타낼 수 있다는 것을 의미하며, 이는 인플레이션율과 디플레이션율이라고 불린다. 반면, 투자의 가치 증가율에는 수익률과 이자율이 포함된다. 보다 구체적으로 수리금융학에서 등비급수는 화폐의 시간가치에도 적용될 수 있다. 즉, 영구연금의 현재가치를 나타내는 데 사용된다. 영구연금은 미래에 무기한으로 매년 지불될 금액의 합계이다. 이러한 종류의 계산은 모기지론과 같은 대출의 연이율을 계산하는 데 사용된다. 또한 예상되는 주식 배당금의 현재 가치나 안정적인 성장률을 가정한 금융자산의 종말 가치를 추정하는 데도 사용될 수 있다. 그러나 이자율이 일정하다는 가정은 일반적으로 옳지 않고, 영구연금 발행자가 계속적인 지불 능력을 상실하거나 약속을 종료할 수 있으므로, 이러한 추정치는 실제 현재 가치에 대한 과학적 예측이라기보다는 의사 결정을 위한 단지 경험적 지침일 뿐이다.

코크 곡선의 내부는 무한히 많은 삼각형의 합집합이다.

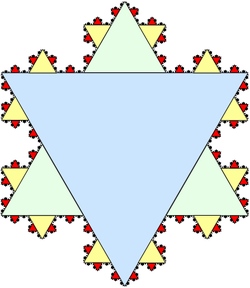
아르키메데스의 포물선 구적법에서 포물선과 직선으로 둘러싸인 면적을 찾는 것 외에도, 등비급수는 무한히 많은 정삼각형의 합집합으로 묘사되는 코크 곡선의 면적을 찾는 데도 적용될 수 있다(그림 참조). 녹색 삼각형의 각 변은 큰 파란색 삼각형의 변 크기의 정확히 ⁠1/3⁠이므로, 면적은 정확히 ⁠1/9⁠이다. 마찬가지로, 각 노란색 삼각형은 녹색 삼각형 면적의 ⁠1/9⁠이며, 그 다음은 계속 이어진다. 이 모든 삼각형은 등비급수로 표현될 수 있다. 파란색 삼각형의 면적이 첫 번째 항이고, 세 개의 녹색 삼각형의 면적이 두 번째 항이며, 열두 개의 노란색 삼각형의 면적이 세 번째 항인 식이다. 초기 1을 제외하고 이 급수는 공비 ${\textstyle r={\frac {4}{9}}}$를 가지며, 파란색 삼각형을 면적 단위로 취하면 눈송이의 총 면적은 다음과 같다. $$1+3\left({\frac {1}{9}}\right)+12\left({\frac {1}{9}}\right)^{2}+48\left({\frac {1}{9}}\right)^{3}+\cdots ={\frac {1}{1-{\frac {4}{9}}}}={\frac {8}{5}}.$$

컴퓨터 과학의 다양한 주제에는 다음과 같은 등비급수의 응용이 포함될 수 있다.

• 알고리즘 분석: 재귀 알고리즘(분할 정복과 같은)의 시간 복잡도를 분석하고, 동적 배열 크기 조정과 같이 비용이 다양한 연산에 대한 분할 상환 분석을 수행한다.
• 자료 구조: 균형 이진 탐색 트리 및 힙과 같은 자료 구조에서 연산의 공간 및 시간 복잡도를 분석한다.
• 컴퓨터 그래픽: 렌더링 알고리즘에서 안티앨리어싱, 밉맵, 그리고 세부 사항의 스케일이 기하학적으로 변하는 프랙탈 생성에 중요하다.
• 네트워킹 및 통신: 지수적 후퇴 알고리즘의 재전송 지연을 모델링하고, 효율적인 통신을 위해 데이터 압축 및 오류 정정 부호에 사용된다.
• 확률적 및 무작위 알고리즘: 무작위 행보, 마르코프 연쇄, 기하 분포를 분석하며, 이는 확률적 및 무작위 알고리즘에 필수적이다.

실수 및 복소수 너머

실수 및 복소수 매개변수 $a$와 $r$를 갖는 등비급수가 가장 일반적이지만, 함수, 행렬, $p$-진수와 같은 더 일반적인 항을 갖는 등비급수도 응용된다. 등비급수를 매개변수로 표현하는 데 사용되는 수학적 연산은 단순히 덧셈과 반복 곱셈이므로, 추상대수학의 맥락에서 임의의 환 또는 체에서 매개변수를 갖는 등비급수를 정의하는 것은 자연스럽다. 반환에서 매개변수를 갖는 등비급수로의 추가 일반화는 더 드물지만, 응용도 있다. 예를 들어, 합리적 급수를 통한 오토마타의 변환에서와 같이 변환 함수의 고정점 반복 연구에서 그렇다.

이러한 일반적인 등비급수의 수렴을 분석하려면 덧셈과 곱셈 외에 급수의 부분합 사이의 거리 측정도 있어야 한다. 이는 함수 급수에서 균등 수렴과 점별 수렴 사이의 구별과 같이 수렴 문제에 새로운 미묘함을 도입할 수 있으며, $a=1$ 및 $r=2$를 갖는 급수 $1+2+4+8+\cdots$가 2진수에서 2진 절댓값을 수렴 측정으로 사용하여 $${\frac {a}{1-r}}=-1$$로 수렴하는 것과 같이 실수로부터의 직관과 강한 대조를 이룰 수 있다. 이 경우, 공통 계수의 2진 절댓값은 $|r|_{2}=|2|_{2}={\tfrac {1}{2}}$이며, 이는 실수 절댓값 관점에서는 직관에 어긋나지만 (여기서 $|2|=2$는 당연하다), P진 해석학의 맥락에서는 충분히 정당화된다.

매개변수의 곱셈이 교환적이지 않을 때, 이는 행렬이나 일반적인 물리 연산자, 특히 양자역학에서는 흔히 그러한데, 등비급수를 쓰는 표준적인 방법인 $$a+ar+ar^{2}+ar^{3}+\cdots ,$$ 오른쪽에서 곱하는 방식은 대체적인 $$a+ra+r^{2}a+r^{3}a+\cdots ,$$ 왼쪽에서 곱하는 방식과, 또한 대칭적인 $$a+r^{\frac {1}{2}}ar^{\frac {1}{2}}+rar+r^{\frac {3}{2}}ar^{\frac {3}{2}}+\cdots ,$$ 각 측면에 절반씩 곱하는 방식과 구별되어야 할 수도 있다. 이러한 선택은 이토 적분과 스트라토노비치 적분에서 미소 시간 스케일에서 드리프트와 확산의 상호 간섭을 다르게 순서화하는 경우와 같이, 응용 분야에서 서로 다른 강점과 약점을 가진 중요한 대안에 해당할 수 있다.

각주

• Andrews, George E. (1998). 《The geometric series in calculus》. 《The American Mathematical Monthly》 105 (Mathematical Association of America). 36–40쪽. doi:10.2307/2589524. JSTOR 2589524. 
• Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 8, 1987.
• Courant, R. and Robbins, H. "The Geometric Progression." §1.2.3 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 13–14, 1996.
• Hall, Brian C. (2015), 《Lie groups, Lie algebras, and representations: An elementary introduction》, Graduate Texts in Mathematics 222 2판, Springer, ISBN 978-3-319-13466-6 
• Horn, Roger A.; Johnson, Charles R. (1990). 《Matrix Analysis》. Cambridge University Press. ISBN 978-0-521-38632-6. .
• James Stewart (2002). Calculus, 5th ed., Brooks Cole. ISBN 978-0-534-39339-7
• Larson, Hostetler, and Edwards (2005). Calculus with Analytic Geometry, 8th ed., Houghton Mifflin Company. ISBN 978-0-618-50298-1
• Pappas, T. "Perimeter, Area & the Infinite Series." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 134–135, 1989.
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), 《College Calculus with Analytic Geometry》 2판, Reading: Addison-Wesley, LCCN 76087042 
• Roger B. Nelsen (1997). Proofs without Words: Exercises in Visual Thinking, The Mathematical Association of America. ISBN 978-0-88385-700-7

역사 및 철학

• C. H. Edwards Jr. (1994). The Historical Development of the Calculus, 3rd ed., Springer. ISBN 978-0-387-94313-8.
• 엘리 마오르 (1991). To Infinity and Beyond: A Cultural History of the Infinite, Princeton University Press. ISBN 978-0-691-02511-7
• Morr Lazerowitz (2000). The Structure of Metaphysics (International Library of Philosophy), Routledge. ISBN 978-0-415-22526-7

경제학

• Carl P. Simon and Lawrence Blume (1994). Mathematics for Economists, W. W. Norton & Company. ISBN 978-0-393-95733-4
• Mike Rosser (2003). Basic Mathematics for Economists, 2nd ed., Routledge. ISBN 978-0-415-26784-7

생물학

• Edward Batschelet (1992). Introduction to Mathematics for Life Scientists, 3rd ed., Springer. ISBN 978-0-387-09648-3
• Richard F. Burton (1998). Biology by Numbers: An Encouragement to Quantitative Thinking, Cambridge University Press. ISBN 978-0-521-57698-7

외부 링크

• “Geometric progression”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Geometric Series”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• “Geometric Series”. 《PlanetMath》 (영어). 
• Peppard, Kim. “College Algebra Tutorial on Geometric Sequences and Series”. West Texas A&M University. 
• Casselman, Bill. “A Geometric Interpretation of the Geometric Series”. 2007년 9월 29일에 원본 문서 (Applet)에서 보존된 문서. 
• "Geometric Series" by Michael Schreiber, 울프람 데몬스트레이션 프로젝트, 2007.