생존 함수

생존 함수(survival function)는 환자, 장치 또는 기타 관심 대상이 특정 시간 이후에도 생존할 확률을 나타내는 함수이다.^[1] 생존 함수는 생존자 함수^[2] 또는 신뢰성 함수^[3]로도 알려져 있다. 신뢰성 함수라는 용어는 공학 분야에서 흔히 사용되는 반면, 생존 함수라는 용어는 인간 사망률을 포함한 더 넓은 범위의 응용 분야에서 사용된다. 생존 함수는 수명의 누적 분포 함수의 여함수이다. 때로는 누적 분포 함수의 여함수를 일반적으로 생존 함수라고 부르기도 한다.

정의

고장까지의 시간을 나타내는 연속 확률 변수 $T$ 가 있다고 하자. 만약 $T$ 가 구간 $[0,\infty )$ 에서 누적 분포 함수 $F(t)$ 와 확률 밀도 함수 $f(t)$ 를 가진다면, 생존 함수 또는 신뢰성 함수는 다음과 같다:

$S(t)=\Pr(T>t)=1-F(t)=1-\int _{0}^{t}f(u)\,du$

생존 함수의 예시

아래 그래프는 가상의 생존 함수 예시를 보여준다. x축은 시간이고, y축은 생존 대상자의 비율이다. 그래프는 대상자가 시간 t를 넘어 생존할 확률을 보여준다.

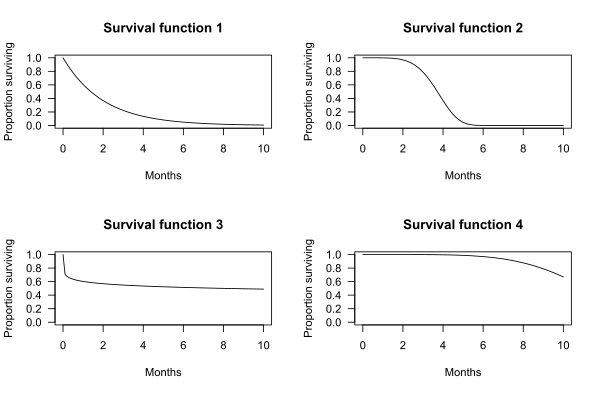
예를 들어, 생존 함수 1의 경우 t = 2개월보다 오래 생존할 확률은 0.37이다. 즉, 대상자의 37%가 2개월 이상 생존한다.

생존 함수 2의 경우 t = 2개월보다 오래 생존할 확률은 0.97이다. 즉, 대상자의 97%가 2개월 이상 생존한다.

중앙 생존 기간은 생존 함수로부터 결정될 수 있다: 중앙 생존 기간은 생존 함수가 0.5 값과 교차하는 지점이다.^[4] 예를 들어, 생존 함수 2의 경우, 대상자의 50%가 3.72개월 생존한다. 따라서 중앙 생존 기간은 3.72개월이다.

중앙 생존 기간은 그래프만으로 항상 결정할 수 있는 것은 아니다. 예를 들어, 생존 함수 4에서는 대상자의 50% 이상이 10개월의 관찰 기간보다 더 오래 생존한다.

생존 함수는 생존 데이터를 설명하고 표시하는 여러 방법 중 하나이다. 데이터를 표시하는 또 다른 유용한 방법은 대상자의 생존 시간 분포를 보여주는 그래프이다. 올킨(Olkin) 등^[5]은 426페이지에서 다음 생존 데이터 예시를 제시한다. 에어컨(AC) 시스템의 연속적인 고장 간 시간(시간, t)이 기록되었다: 1, 3, 5, 7, 11, 11, 11, 12, 14, 14, 14, 16, 16, 20, 21, 23, 42, 47, 52, 62, 71, 71, 87, 90, 95, 120, 120, 225, 246, 261. 평균 고장 간 시간은 59.6시간이다. 아래 그림은 고장 간 시간 분포를 보여준다. 그래프 아래의 파란색 눈금 표시는 연속적인 AC 고장 간 실제 시간을 나타낸다.

이 예시에서는 지수 분포를 나타내는 곡선이 AC 고장 시간 분포 위에 겹쳐져 있으며, 지수 분포는 AC 고장 시간 분포를 근사한다. 이 특정 지수 곡선은 파라미터 람다, λ로 지정된다.

λ = 1/(평균 고장 간 시간) = 1/59.6 = 0.0168.

시간은 양의 값을 가질 수 있으므로 고장 시간의 분포는 확률 밀도 함수(PDF)이다. 방정식에서 PDF는 f_T로 지정된다. 만약 시간이 (1일, 2일 등과 같이) 이산적인 값만 가질 수 있다면, 고장 시간의 분포를 확률 질량 함수라고 부른다. 대부분의 생존 분석 방법은 시간이 어떤 양수 값도 가질 수 있다고 가정하며, f_T는 PDF이다. 관찰된 AC 고장 간 시간이 지수 함수를 사용하여 근사된다면, 지수 곡선은 AC 고장 시간의 확률 밀도 함수 f_T를 제공한다.

생존 데이터를 표시하는 또 다른 유용한 방법은 각 시점까지의 누적 고장을 보여주는 그래프이다. 이 데이터는 각 시점까지의 누적 고장 수 또는 누적 고장 비율로 표시될 수 있다. 아래 그래프는 에어컨 시스템의 각 시점에서의 누적 고장 확률(또는 비율)을 보여준다. 검은색 계단형 선은 누적 고장 비율을 나타낸다. 각 계단마다 그래프 하단에 관찰된 고장 시간을 나타내는 파란색 눈금 표시가 있다. 부드러운 빨간색 선은 관찰된 데이터에 적합된 지수 곡선을 나타낸다.

각 시점까지의 누적 고장 확률 그래프를 누적 분포 함수(CDF)라고 한다. 생존 분석에서 누적 분포 함수는 생존 시간이 특정 시간 t보다 작거나 같을 확률을 나타낸다.

생존 시간 T를 양의 정수라고 하자. 특정 시간은 소문자 t로 표시된다. T의 누적 분포 함수는 다음 함수이다.

$F(t)=\Pr(T\leq t),$

여기서 우변은 확률 변수 T가 t보다 작거나 같을 확률을 나타낸다. 시간이 어떤 양수 값도 가질 수 있다면, 누적 분포 함수 F(t)는 확률 밀도 함수 f(t)의 적분이다.

에어컨 예시에서, 아래 CDF 그래프는 데이터에 적합된 지수 곡선을 사용하여 추정했을 때, 고장 시간이 100시간 이하일 확률이 0.81임을 보여준다.

고장 시간이 100시간 이하일 확률을 그래프로 나타내는 것의 대안은 고장 시간이 100시간보다 길 확률을 그래프로 나타내는 것이다. 총 확률은 1이 되어야 하므로, 고장 시간이 100시간보다 길 확률은 고장 시간이 100시간 이하일 확률을 1에서 뺀 값과 같아야 한다.

따라서 다음과 같다:

${\begin{aligned}\Pr({\text{failure times}}>100{\text{ hours}})&=1-\Pr({\text{failure times}}\leq 100{\text{ hours}})\\&=1-0.81=0.19\end{aligned}}$

이 관계는 모든 고장 시간에 대해 일반화된다:

$\Pr(T>t)=1-\Pr(T\leq t)={\text{ cumulative distribution function.}}$

이 관계는 아래 그래프에 나와 있다. 왼쪽 그래프는 Pr(T ≤ t)인 누적 분포 함수이다. 오른쪽 그래프는 Pr(T > t) = 1 − Pr(T ≤ t)이다. 오른쪽 그래프는 생존 함수 S(t)이다. S(t) = 1 – CDF라는 사실이 생존 함수가 여누적 분포 함수라고 불리는 이유이다.

모수적 생존 함수

에어컨 예시와 같은 일부 경우, 생존 시간 분포는 지수 분포와 같은 함수에 의해 잘 근사될 수 있다. 지수 분포, 베이불 분포, 감마, 정규, 로그정규, 로그로지스틱을 포함한 여러 분포가 생존 분석에서 일반적으로 사용된다.^[3]^[6] 이 분포들은 매개변수에 의해 정의된다. 예를 들어, 정규(가우스) 분포는 평균과 표준 편차라는 두 매개변수에 의해 정의된다. 매개변수에 의해 정의되는 생존 함수를 모수적(parametric)이라고 한다.

위에서 보여준 네 가지 생존 함수 그래프에서 생존 함수의 모양은 특정 확률 분포에 의해 정의된다. 생존 함수 1은 지수 분포에 의해, 2는 베이불 분포에 의해, 3은 로그로지스틱 분포에 의해, 4는 또 다른 베이불 분포에 의해 정의된다.

지수 생존 함수

지수 생존 분포의 경우, 개체나 장치의 연령에 관계없이 모든 시간 간격에서 고장 확률은 동일하다. 이 사실은 지수 생존 분포의 "기억상실" 속성으로 이어진다: 대상의 연령은 다음 시간 간격의 고장 확률에 영향을 미치지 않는다. 지수 분포는 부품이 고장나면 교체되는 시스템의 수명에 대한 좋은 모델이 될 수 있다.^[7] 또한 짧은 간격 동안 살아있는 유기체의 생존을 모델링하는 데 유용할 수 있다. 그러나 살아있는 유기체의 전체 수명을 모델링하는 데는 좋은 모델이 아닐 수 있다.^[8] 에프론(Efron)과 해스티(Hastie)^[9] (p. 134)가 지적했듯이, "인간의 수명이 지수적이라면, 노인이나 젊은 사람은 없고, 그저 운이 좋거나 운이 없는 사람들만 있을 것이다."

베이불 생존 함수

지수 생존 함수의 주요 가정은 위험률이 일정하다는 것이다. 위에서 주어진 예시에서 매년 사망하는 남성의 비율은 10%로 일정했으며, 이는 위험률이 일정하다는 것을 의미한다. 일정한 위험률이라는 가정은 적절하지 않을 수 있다. 예를 들어, 대부분의 살아있는 유기체에서는 노년기의 사망 위험이 중년기보다 크다. 즉, 위험률이 시간에 따라 증가한다. 유방암과 같은 일부 질병에서는 재발 위험이 5년 후에는 낮아진다. 즉, 위험률이 시간에 따라 감소한다. 베이불 분포는 지수 분포를 확장하여 위험률이 일정하거나, 증가하거나, 감소할 수 있도록 한다.

기타 모수적 생존 함수

특정 데이터 세트에 더 잘 맞는 다른 모수적 생존 함수로는 정규, 로그정규, 로그로지스틱, 감마 등이 있다. 특정 응용 분야에 대한 모수 분포 선택은 그래프 방법이나 공식적인 적합도 검정을 사용하여 수행할 수 있다. 이러한 분포와 검정은 생존 분석 교과서에 설명되어 있다.^[1]^[3] 로리스(Lawless)^[10]는 모수적 모델에 대해 광범위하게 다루고 있다.

모수적 생존 함수는 주로 관찰 기간을 넘어 생존 함수를 추정할 수 있게 해주기 때문에 제조 응용 분야에서 흔히 사용된다. 그러나 모수적 함수의 적절한 사용은 데이터가 선택된 분포에 의해 잘 모델링될 것을 요구한다. 적절한 분포를 사용할 수 없거나 임상 시험 또는 실험 전에 지정할 수 없는 경우, 비모수적 생존 함수는 유용한 대안을 제공한다.

비모수적 생존 함수

생존에 대한 모수적 모델이 불가능하거나 바람직하지 않을 수 있다. 이러한 상황에서 생존 함수를 모델링하는 가장 일반적인 방법은 비모수적 카플란-마이어 생존분석이다. 이 추정량은 수명 데이터를 필요로 한다. 주기적인 사례(코호트) 및 사망(및 회복) 횟수는 수명 데이터 없이 생존 함수의 비모수적 최대 가능도 및 최소 제곱 추정치를 만드는 데 통계적으로 충분하다.

속성

모든 생존 함수 $S(t)$ $S(t)$ 는 단조 감소한다. 즉, 모든 $u>t$ $u>t$ 에 대해 $S(u)\leq S(t)$ $S(u)\leq S(t)$ 이다.
- 이는 일반적으로 사망률 또는 일부 시스템의 고장과 관련된 일련의 이벤트를 시간에 매핑하는 확률 변수의 속성이다.
시간 $t=0$ 은 일반적으로 연구의 시작 또는 일부 시스템의 작동 시작을 나타내는 기점을 나타낸다. $S(0)$ 은 일반적으로 1이지만, 시스템이 작동 즉시 고장날 확률을 나타내기 위해 더 작을 수 있다.
CDF는 우연속 함수이므로, 생존 함수 $S(t)=1-F(t)$ 도 우연속이다.
생존 함수는 확률 밀도 함수 $f(t)$ $f(t)$ 및 위험 함수 $\lambda (t)$ $\lambda (t)$ 와 관련될 수 있다.
- $f(t)=-S'(t)$
- $\lambda (t)=-{\frac {d}{dt}}\log S(t)$

따라서 $S(t)=\exp \left[-\int _{0}^{t}\lambda (t')\,dt'\right]$

기대 생존 시간 $\mathbb {E} (T)=\int _{0}^{\infty }S(t)\,dt$

이 글을 보려면 오른쪽 ‘펼치기’ 버튼 클릭

확률 변수

T\in [0,\infty )

의 기댓값은 다음과 같이 정의된다.

$\mathbb {E} (T)=\int _{0}^{\infty }tf(t)\,dt$

여기서 $f(t)$ 는 확률 밀도 함수이다. 관계 $f(t)=-S'(t)$ 를 사용하여 기댓값 공식을 수정할 수 있다.

$\mathbb {E} (T)=-\int _{0}^{\infty }tS'(t)\,dt$

이는 부분 적분을 사용하여 더욱 단순화될 수 있다.

$-\int _{0}^{\infty }tS'(t)\,dt=-tS(t){\bigg |}_{0}^{\infty }+\int _{0}^{\infty }S(t)\,dt$

정의에 따라 $S(\infty )=0$ 이므로 경계 항은 동일하게 0이 된다. 따라서 기댓값은 단순히 생존 함수의 적분이라는 결론을 내릴 수 있다.

$\mathbb {E} (T)=\int _{0}^{\infty }S(t)\,dt$

같이 보기

각주

↑ ^가 ^나 Kleinbaum, David G.; Klein, Mitchel (2012), 《Survival analysis: A Self-learning text》 Thi판, Springer, ISBN 978-1441966452
↑ Tableman, Mara; Kim, Jong Sung (2003), 《Survival Analysis Using S》 Fir판, Chapman and Hall/CRC, ISBN 978-1584884088
↑ ^가 ^나 ^다 Ebeling, Charles (2010), 《An Introduction to Reliability and Maintainability Engineering》 Seco판, Waveland Press, ISBN 978-1577666257
↑ Machin, D., Cheung, Y. B., Parmar, M. (2006). Survival Analysis: A Practical Approach. Deutschland: Wiley. Page 36 and following Google Books
↑ Olkin, Ingram; Gleser, Leon; Derman, Cyrus (1994), 《Probability Models and Applications》 Seco판, Macmillan, ISBN 0-02-389220-X
↑ Klein, John; Moeschberger, Melvin (2005), 《Survival Analysis: Techniques for Censored and Truncated Data》 Seco판, Springer, ISBN 978-0387953991
↑ Mendenhall, William; Terry, Sincich (2007), 《Statistics for Engineering and the Sciences》 Fif판, Pearson / Prentice Hall, ISBN 978-0131877061
↑ Brostrom, Göran (2012), 《Event History Analysis with R》 Fir판, Chapman & Hall/CRC, ISBN 978-1439831649
↑ Efron, Bradley; Hastie, Trevor (2016), 《Computer Age Statistical Inference: Algorithms, Evidence, and Data Science》 Fir판, Cambridge University Press, ISBN 978-1107149892
↑ Lawless, Jerald (2002), 《Statistical Models and Methods for Lifetime Data》 Seco판, Wiley, ISBN 978-0471372158

[KleinbaumKlein2012-1] 가 ^나 Kleinbaum, David G.; Klein, Mitchel (2012), 《Survival analysis: A Self-learning text》 Thi판, Springer, ISBN 978-1441966452

[TablemanKim2003-2] Tableman, Mara; Kim, Jong Sung (2003), 《Survival Analysis Using S》 Fir판, Chapman and Hall/CRC, ISBN 978-1584884088

[Ebeling2010-3] 가 ^나 ^다 Ebeling, Charles (2010), 《An Introduction to Reliability and Maintainability Engineering》 Seco판, Waveland Press, ISBN 978-1577666257

[4] Machin, D., Cheung, Y. B., Parmar, M. (2006). Survival Analysis: A Practical Approach. Deutschland: Wiley. Page 36 and following Google Books

[OlkinGleserDerman1994-5] Olkin, Ingram; Gleser, Leon; Derman, Cyrus (1994), 《Probability Models and Applications》 Seco판, Macmillan, ISBN 0-02-389220-X

[Klein2005-6] Klein, John; Moeschberger, Melvin (2005), 《Survival Analysis: Techniques for Censored and Truncated Data》 Seco판, Springer, ISBN 978-0387953991

[Mendenhall2007-7] Mendenhall, William; Terry, Sincich (2007), 《Statistics for Engineering and the Sciences》 Fif판, Pearson / Prentice Hall, ISBN 978-0131877061

[Brostrom2012-8] Brostrom, Göran (2012), 《Event History Analysis with R》 Fir판, Chapman & Hall/CRC, ISBN 978-1439831649

[EfronHastie2016-9] Efron, Bradley; Hastie, Trevor (2016), 《Computer Age Statistical Inference: Algorithms, Evidence, and Data Science》 Fir판, Cambridge University Press, ISBN 978-1107149892

[Lawless2002-10] Lawless, Jerald (2002), 《Statistical Models and Methods for Lifetime Data》 Seco판, Wiley, ISBN 978-0471372158

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]