핵 결합 에너지
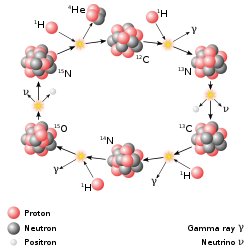 |
|
방사성 붕괴 핵분열 핵융합 |
실험물리학에서 핵 결합 에너지(영어: Nuclear binding energy)는 원자의 원자핵을 구성하는 양성자와 중성자(총칭하여 핵자라고 함)로 분해하는 데 필요한 최소 에너지이다. 안정된 핵의 경우 결합 에너지는 항상 양수인데, 이는 핵자들이 서로 멀어지기 위해서는 핵이 에너지를 얻어야 하기 때문이다. 핵자들은 강한 핵력에 의해 서로 끌어당겨진다. 이론 핵물리학에서는 핵 결합 에너지를 음수로 간주한다. 이 맥락에서 핵 결합 에너지는 핵이 구성 핵자들과 무한히 멀리 떨어져 있을 때의 핵자에 대한 핵의 에너지를 나타낸다. 실험적 관점과 이론적 관점은 결합 에너지가 무엇을 의미하는지에 대해 약간 다른 강조점을 가지고 있지만 동등하다.
원자핵의 질량은 자유로운 구성 양성자와 중성자의 개별 질량의 합보다 작다. 이 질량 차이는 아인슈타인 방정식, E = mc2으로 계산할 수 있으며, 여기서 E는 핵 결합 에너지, c는 빛의 속력, m은 질량 차이이다. 이 "사라진 질량"은 질량 결손으로 알려져 있으며, 핵이 형성될 때 방출된 에너지를 나타낸다.[1]
"핵 결합 에너지"라는 용어는 핵이 하나 이상의 핵자로 구성된 조각으로 쪼개지는 과정에서의 에너지 균형을 의미할 수도 있다. 가벼운 핵이 융합하거나(핵융합), 무거운 핵이 분열할 때(핵분열) 새로운 결합 에너지가 발생하면, 두 과정 모두 이 결합 에너지의 방출을 초래할 수 있다. 이 에너지는 핵 에너지로 활용될 수 있으며, 원자력이나 핵무기에서처럼 전기를 생산하는 데 사용될 수 있다. 큰 핵이 분열할 때, 과잉 에너지는 감마선과 다양한 방출 입자(핵분열 생성물)의 운동 에너지로 방출된다.
이러한 핵 결합 에너지와 핵력은 수소와 같은 가벼운 원자의 전자 결합 에너지보다 백만 배 정도 더 크다.[2]
서론
[편집]핵 에너지
[편집]핵 에너지의 흡수 또는 방출은 핵반응이나 방사성 붕괴에서 발생한다. 에너지를 흡수하는 반응은 흡열 반응이라고 불리며, 에너지를 방출하는 반응은 발열 반응이라고 불린다. 에너지가 소비되거나 방출되는 것은 핵변환의 들어오는 생성물과 나가는 생성물 사이의 핵 결합 에너지 차이 때문이다.[3]
가장 잘 알려진 발열 핵변환 유형은 핵분열과 핵융합이다. 핵분열에 의해 핵 에너지가 방출될 수 있는데, 이는 무거운 원자핵(우라늄과 플루토늄과 같은)이 가벼운 핵으로 쪼개질 때 발생한다. 핵분열로부터의 에너지는 전 세계 수백 곳에서 전력을 생산하는 데 사용된다. 핵 에너지는 또한 핵융합 과정에서 방출되는데, 이는 수소와 같은 가벼운 원자핵이 결합하여 헬륨과 같은 더 무거운 핵을 형성할 때 발생한다. 태양과 다른 항성들은 핵융합을 사용하여 열 에너지를 생성하고, 이 열 에너지는 표면에서 복사되는데, 이는 항성 핵합성의 한 유형이다. 모든 발열 핵 과정에서 핵 질량은 궁극적으로 열 에너지로 변환되어 열로 방출될 수 있다.
어떤 핵변환에서 방출되거나 흡수되는 에너지를 정량화하기 위해서는 해당 변환에 관련된 핵 구성 요소의 핵 결합 에너지를 알아야 한다.
핵력
[편집]전자와 핵은 정전기적 인력(음전하는 양전하를 끌어당김)에 의해 함께 유지된다. 또한, 전자는 때때로 인접 원자에 의해 공유되거나 그 원자로 전달되기도 하는데(양자 물리학 과정에 의해), 원자 간의 이러한 연결을 화학 결합이라고 하며 모든 화합물의 형성을 담당한다.[4]
전기력은 핵을 붙잡아 두지 못하는데, 모든 양성자가 양전하를 띠고 서로 반발하기 때문이다. 만약 두 양성자가 접촉한다면, 그들의 반발력은 거의 40뉴턴에 달할 것이다. 중성자 각각이 총 전하가 0이기 때문에, 양성자가 중성자를 전기적으로 분극시키도록 유도할 수 있다면 양성자는 중성자를 전기적으로 끌어당길 수 있을 것이다. 그러나 두 양성자 사이에 중성자를 두면(서로 간의 반발력이 10N으로 감소) 전기 사중극자 (− + + −) 배열에서만 중성자를 끌어당길 것이다. 더 많은 양성자를 만족시키기 위해 필요한 고차 다중극자는 약한 인력을 유발하며, 빠르게 비현실적이 된다.
양성자 및 중성자 자기 모멘트가 측정되고 확인된 후, 그들의 자기력이 20 또는 30 뉴턴에 달할 수 있으며, 적절하게 정렬되면 인력이 된다는 것이 명백해졌다. 한 쌍의 양성자는 서로 접근할 때 10−13줄의 일을 할 것이다. 즉, 그들은 서로 붙어 있기 위해 0.5 MeV의 에너지를 방출해야 할 것이다. 반면에, 일단 한 쌍의 핵자가 자기적으로 붙으면, 그들의 외부장은 크게 감소하여, 많은 핵자가 많은 자기 에너지를 축적하기 어렵다.
따라서, 다른 힘인 핵력(또는 잔류 강한 힘)이 핵의 핵자들을 함께 묶어준다. 이 힘은 강한 상호작용의 잔류물이며, 강한 상호작용은 더 작은 거리 수준에서 쿼크를 핵자 내부로 묶어준다.
핵이 정상적인 조건에서 뭉치지 않는(융합하지 않는)다는 사실은 핵력이 먼 거리에서는 전기적 반발력보다 약하지만, 가까운 거리에서는 더 강해야 한다는 것을 시사한다. 따라서 핵력은 단거리 특성을 갖는다. 핵력에 대한 비유는 두 개의 작은 자석 사이의 힘과 같다: 자석은 서로 붙어 있을 때 분리하기가 매우 어렵지만, 짧은 거리만큼 떨어뜨리면 그들 사이의 힘은 거의 0으로 떨어진다.[4]
중력이나 전기력과 달리 핵력은 매우 짧은 거리에서만 효과적이다. 더 먼 거리에서는 정전기력이 우세하다. 양성자는 양전하를 띠고 같은 전하는 서로 반발하기 때문에 서로 밀어낸다. 이런 이유로, 예를 들어 수소로 채워진 풍선 안에 있는 일반 수소의 핵을 구성하는 양성자들은 헬륨을 형성하기 위해 결합하지 않는다(이 과정은 또한 일부 양성자들이 전자와 결합하여 중성자가 되어야 한다). 그들은 서로를 끌어당기는 핵력이 중요해질 만큼 충분히 가까워질 수 없다. 오직 극심한 압력과 온도의 조건에서만(예: 항성의 핵 내부) 이러한 과정이 일어날 수 있다.[5]
핵 물리학
[편집]지구상에는 약 94개의 자연 발생 원소가 있다. 각 원소의 원자는 특정 수의 양성자 (주어진 원소에 대해 항상 동일한 수)와 대략 비슷한 수의 중성자를 포함하는 원자핵을 가지고 있다. 동일한 원소의 두 원자가 서로 다른 수의 중성자를 가질 경우, 이들은 해당 원소의 동위 원소라고 알려져 있다. 다른 동위 원소는 다른 특성을 가질 수 있다. 예를 들어, 하나는 안정적일 수 있고 다른 하나는 불안정하여 점차적으로 방사성 붕괴를 거쳐 다른 원소가 될 수 있다.
수소 핵은 단 하나의 양성자로 이루어져 있다. 수소의 동위 원소인 중수소 또는 무거운 수소는 양성자 하나와 중성자 하나를 포함한다. 헬륨의 가장 흔한 동위 원소는 양성자 두 개와 중성자 두 개를 포함하며, 탄소, 질소, 산소는 각각 양성자와 중성자를 여섯, 일곱, 여덟 개씩 포함한다. 그러나 헬륨 핵은 그것을 구성하는 두 개의 무거운 수소 핵의 무게 합보다 적게 나간다.[6] 탄소, 질소, 산소의 경우에도 마찬가지이다. 예를 들어, 탄소 핵은 탄소 핵을 만들기 위해 결합할 수 있는 세 개의 헬륨 핵보다 약간 가볍다. 이 차이를 질량 결손이라고 한다.
질량 결손
[편집]질량 결손(또는 "질량 부족")은 물체의 질량과 그 구성 입자들의 질량 합계 사이의 차이이다. 1905년에 알베르트 아인슈타인에 의해 발견되었으며, E = mc2라는 그의 공식으로 설명될 수 있는데, 이는 에너지와 질량의 등가성을 기술한다. 질량의 감소는 원자 생성 반응에서 방출된 에너지를 c2으로 나눈 것과 같다.[7] 이 공식에 따르면, 에너지를 추가하면 질량도 증가하고(무게와 관성 모두), 에너지를 제거하면 질량은 감소한다. 예를 들어, 네 개의 핵자를 포함하는 헬륨 원자는 네 개의 수소 원자(각각 하나의 핵자를 포함)의 총 질량보다 약 0.8% 적은 질량을 가진다. 헬륨 핵은 함께 묶인 네 개의 핵자를 가지며, 이들을 묶어주는 결합 에너지는 사실상 사라진 질량의 0.8%이다.[8][9]
더 가벼운 원소의 경우, 더 가벼운 원소에서 이들을 조립함으로써 방출될 수 있는 에너지는 감소하며, 융합할 때 에너지가 방출될 수 있다. 이는 철/니켈보다 가벼운 핵에 해당한다. 더 무거운 핵의 경우, 이들을 결합하는 데 더 많은 에너지가 필요하며, 이 에너지는 이들을 조각으로 분해함으로써 방출될 수 있다(핵분열로 알려져 있다). 원자력은 현재 원자력 발전소에서 우라늄 핵을 분해하고 방출된 에너지를 열로 포획하여 전기로 변환함으로써 생성된다.
일반적으로 매우 가벼운 원소는 비교적 쉽게 융합할 수 있고, 매우 무거운 원소는 핵분열을 통해 매우 쉽게 부서질 수 있다. 중간에 있는 원소는 더 안정적이며 실험실과 같은 환경에서는 융합이나 핵분열을 일으키기 어렵다.
철 이후에 이러한 경향이 역전되는 이유는 핵의 양전하가 증가하여 핵이 분열하는 경향이 생기기 때문이다. 이는 핵자들을 결합시키는 강한 핵 상호작용에 의해 저항받는다. 전기력은 강한 핵력보다 약할 수 있지만, 강한 힘은 훨씬 더 제한적인 범위를 갖는다. 철 핵에서는 각 양성자가 다른 25개의 양성자를 밀어내지만, 핵력은 가까운 이웃만 결합시킨다. 따라서 더 큰 핵의 경우, 정전기력이 지배하는 경향이 있으며 핵은 시간이 지남에 따라 분열하는 경향이 있다.
핵이 더욱 커질수록, 이러한 파괴적 효과는 점차적으로 더욱 중요해진다. 폴로늄(84개의 양성자)에 이르면, 핵은 더 이상 큰 양전하를 수용할 수 없게 되며, 알파 방사능 과정(각각 두 개의 양성자와 두 개의 중성자를 포함하는 헬륨 핵의 방출)으로 과잉 양성자를 상당히 빠르게 방출한다. (헬륨 핵은 특히 안정적인 조합이다.) 이 과정 때문에 94개 이상의 양성자를 가진 핵은 지구상에서 자연적으로 발견되지 않는다(주기율표 참조). 우라늄(원자 번호 92)을 넘어 가장 긴 반감기를 가진 동위 원소는 플루토늄-244(8천만 년)와 퀴륨-247(1천6백만 년)이다.
태양의 핵반응
[편집]핵융합 과정은 다음과 같이 작동한다: 50억 년 전, 중력이 광대한 성간 기체와 먼지 구름을 끌어당겨 새로운 태양이 형성되었고, 이로부터 지구와 다른 행성들도 생겨났다. 중력은 에너지를 방출하고 초기 태양을 가열했는데, 이는 헬름홀츠가 제안한 방식과 매우 유사하다.[10]
열 에너지는 원자와 분자의 운동으로 나타난다. 입자들의 온도가 높을수록 그들의 속도는 더 커지고 충돌은 더 격렬해진다. 새로 형성된 태양의 중심부 온도가 충분히 높아져 수소 핵들 간의 충돌이 그들의 전기적 반발력을 극복하고 인력적인 핵력의 짧은 범위 내로 들어오게 되자, 핵들은 서로 붙기 시작했다. 이것이 시작되자 양성자들은 중수소와 헬륨으로 결합되었고, 그 과정에서 일부 양성자들은 중성자로 변환되었다(양전자, 즉 양의 전자가 전자와 결합하여 감마선 광자로 소멸). 이 방출된 핵 에너지는 이제 태양 핵의 높은 온도를 유지하고, 이 열은 또한 기체 압력을 높게 유지하여 태양을 현재 크기로 유지하며, 중력이 더 이상 태양을 압축하는 것을 막는다. 이제 중력과 압력 사이에 안정적인 균형이 존재한다.
태양 존재의 다른 단계에서는 다른 핵반응이 우세할 수 있으며, 여기에는 양성자-양성자 반응과 탄소-질소 순환이 포함된다. 이 순환은 더 무거운 핵을 포함하지만, 최종 생성물은 여전히 양성자가 결합하여 헬륨을 형성하는 것이다.
물리학의 한 분야인 제어 핵융합 연구는 1950년대부터 작은 핵을 더 큰 핵으로 결합하는 핵융합 반응으로부터 유용한 에너지를 얻으려고 노력해 왔다. 일반적으로는 보일러를 가열하여 증기로 터빈을 돌려 전기를 생산하는 방식이다. 지구상의 어떤 실험실도 태양 발전소의 한 가지 특징, 즉 뜨거운 플라즈마를 압축하고 핵 융합로를 태양의 핵에 가두는 태양의 거대한 질량을 따라갈 수 없다. 대신 물리학자들은 강력한 자기장을 사용하여 플라즈마를 가두고, 연료로는 더 쉽게 연소되는 무거운 수소 형태를 사용한다. 자기 트랩은 다소 불안정할 수 있으며, 핵융합을 일으킬 만큼 충분히 뜨겁고 밀도가 높은 플라즈마는 짧은 시간 후에 트랩에서 빠져나가는 경향이 있다. 정교한 기술을 사용하더라도 대부분의 경우 구속 시간은 불과 몇 분의 1초에 불과하다.
핵 결합
[편집]수소보다 큰 작은 핵은 더 큰 핵으로 결합하여 에너지를 방출할 수 있지만, 이러한 핵을 결합할 때 방출되는 에너지의 양은 수소 융합에 비해 훨씬 작다. 그 이유는 전체 과정이 핵 인력이 작동하게 하여 에너지를 방출하지만, 먼저 양전하를 띠고 서로 전기적으로 반발하는 양성자들을 강제로 결합시키기 위해 에너지를 주입해야 하기 때문이다.[5]
철(26개의 양성자를 가진 핵)보다 무거운 원소의 경우, 핵융합 과정은 더 이상 에너지를 방출하지 않는다. 더 무거운 핵에서는 비슷한 크기의 핵을 결합함으로써 에너지가 소비되고 방출되지 않는다. 이러한 큰 핵의 경우, 전기적 반발(핵 내 모든 양성자에 영향을 미침)을 극복하는 데 필요한 에너지가 핵 인력(주로 가까운 이웃 사이에서 효과적임)에 의해 방출되는 에너지보다 많다. 반대로, 철보다 무거운 핵을 분해함으로써 실제로 에너지가 방출될 수 있다.[5]
납보다 무거운 원소의 핵에서는 전기적 반발이 너무 강해서 일부 핵은 자발적으로 양의 파편을 방출하는데, 보통 두 개의 양성자와 두 개의 중성자로 구성된 안정적인 알파 입자를 형성하는 헬륨 핵이다. 이러한 자발적인 분열은 일부 핵이 나타내는 방사성의 한 형태이다.[5]
납보다 무거운 핵(비스무트, 토륨, 우라늄 제외)은 너무 빨리 자발적으로 붕괴하여 자연에서 원시 핵종으로 나타나지 않지만, 인위적으로 생성되거나 더 무거운 원소의 붕괴 사슬의 중간체로 생성될 수 있다. 일반적으로 핵이 무거울수록 더 빨리 자발적으로 붕괴한다.[5]
철 핵은 가장 안정적인 핵이며(특히 철-56), 따라서 가장 좋은 에너지원은 철로부터 가능한 한 멀리 떨어진 질량을 가진 핵이다. 가장 가벼운 핵인 수소 핵(양성자)을 결합하여 헬륨 핵을 형성할 수 있으며, 태양은 그렇게 에너지를 생성한다. 또는 가장 무거운 핵인 우라늄 또는 플루토늄 핵을 더 작은 조각으로 분해할 수 있으며, 이것이 원자로가 하는 일이다.[5]
핵 결합 에너지
[편집]핵 결합 에너지를 설명하는 예로는 6개의 양성자와 6개의 중성자를 포함하는 12C(탄소-12)의 핵이 있다. 양성자는 모두 양전하를 띠고 서로 밀어내지만, 핵력이 반발력을 극복하고 양성자를 결합시킨다. 핵력은 근거리 힘이며(1.0 fm 거리에서 강하게 인력적이며 2.5 fm를 넘어가면 매우 작아진다), 핵 외부에서는 이 힘의 효과가 거의 관찰되지 않는다. 핵력은 또한 중성자들을 함께 끌어당기거나, 중성자와 양성자들을 함께 끌어당긴다.[11]
핵의 에너지는 입자들이 무한히 떨어진 거리로 분리될 때의 에너지에 비하면 음수이다(태양계 행성들의 중력 에너지와 마찬가지로). 핵을 개별 양성자와 중성자로 분리하기 위해서는 에너지가 사용되어야 하기 때문이다. 질량 분석기는 핵의 질량을 측정했는데, 이는 항상 핵을 구성하는 양성자와 중성자의 질량 합보다 작으며, 이 차이는 E = mc2 공식에 따라 핵의 결합 에너지를 제공한다.[11]
핵융합
[편집]헬륨의 결합 에너지는 태양과 대부분의 항성의 에너지원이다.[12] 태양은 (질량 기준으로) 74%의 수소로 구성되어 있으며, 수소는 단일 양성자로 이루어진 핵을 가진 원소이다. 태양에서는 4개의 양성자가 헬륨 핵으로 결합될 때 에너지가 방출되는데, 이 과정에서 2개의 양성자도 중성자로 변환된다.[11]
양성자가 중성자로 전환되는 것은 약한 핵력이라는 또 다른 핵력의 결과이다. 약한 핵력은 강한 핵력과 마찬가지로 짧은 범위의 힘이지만, 강한 핵력보다 훨씬 약하다. 약한 핵력은 중성자와 양성자의 수를 에너지적으로 가장 안정적인 구성으로 만들려고 한다. 40개 미만의 입자를 포함하는 핵의 경우, 이 숫자는 보통 거의 같다. 양성자와 중성자는 밀접하게 관련되어 있으며, 총칭하여 핵자라고 알려져 있다. 입자의 수가 약 209개까지 증가함에 따라 안정성을 유지하기 위한 중성자의 수가 양성자의 수를 능가하기 시작하며, 중성자 대 양성자 비율이 약 3대 2에 이른다.[11]
수소의 양성자는 서로의 상호 반발력을 극복하고 강한 핵 인력 범위 내로 들어올 만큼 충분한 속도를 가질 때만 헬륨으로 결합된다. 이는 융합이 매우 뜨거운 기체 내에서만 발생한다는 것을 의미한다. 헬륨으로 결합될 만큼 뜨거운 수소는 이를 가두기 위한 엄청난 압력을 필요로 하지만, 이러한 조건은 태양의 중앙 영역에 존재하며, 이 압력은 핵 위의 층들의 엄청난 무게에 의해 태양의 강한 중력에 의해 안쪽으로 가해진다. 양성자를 결합하여 헬륨을 형성하는 과정은 핵융합의 한 예이다.[11]
지구상에서 일반 수소로부터 헬륨을 생산하는 것은 중수소를 생성하는 어려움 때문에 거의 불가능할 것이다. 중수소와 삼중수소를 사용하는 공정을 개발하기 위한 연구가 진행 중이다. 지구의 바다에는 사용할 수 있는 많은 양의 중수소가 포함되어 있으며, 삼중수소는 리튬으로부터 원자로 내에서 직접 만들 수 있고, 게다가 헬륨 생성물은 환경에 해를 끼치지 않으므로 일부는 핵융합이 우리의 에너지 수요를 충족시키는 좋은 대안이라고 생각한다. 이러한 형태의 융합을 수행하기 위한 실험은 아직 부분적으로만 성공했다. 충분히 뜨거운 중수소와 삼중수소를 가두어야 한다. 한 가지 기술은 매우 강한 자기장을 사용하는 것이다. 왜냐하면 대전된 입자(지구의 방사선대_방사선대에 갇힌 것과 같은)는 자기장 선에 의해 유도되기 때문이다.[11]
결합 에너지 최대치와 붕괴를 통한 접근 방식
[편집]탄소, 질소, 산소와 같은 가벼운 원소의 주요 동위 원소에서는 중성자와 양성자의 가장 안정적인 조합은 그 수가 같을 때 발생한다(이는 원소 20, 칼슘까지 계속된다). 그러나 더 무거운 핵에서는 양성자가 작은 부피에 갇혀 서로 반발하기 때문에 양성자의 파괴 에너지가 증가한다. 핵을 함께 붙잡는 강한 핵력의 에너지도 증가하지만, 속도는 더 느리다. 마치 핵 내부에서 서로 가까운 핵자들만 강하게 결합되어 있고, 더 멀리 떨어진 핵자들은 그렇지 않은 것처럼 보인다.[11]
핵의 순수 결합 에너지는 핵 인력에서 전기력의 파괴 에너지를 뺀 값이다. 헬륨보다 무거운 핵이 될수록 핵자당 순수 결합 에너지(핵의 질량과 구성 핵자 질량의 합계 차이로부터 유추됨)는 점점 더 느리게 증가하여 철에서 최고점에 이른다. 핵자를 추가하면 총 핵 결합 에너지는 항상 증가하지만, 전기력(양성자 간의 반발력)의 총 파괴 에너지도 증가하며, 철을 넘어서면 두 번째 증가가 첫 번째 증가보다 커진다. 철-56 (56Fe)은 가장 효율적으로 결합된 핵이며[11] 이는 핵자당 평균 질량이 가장 적다는 것을 의미한다. 그러나 니켈-62는 핵자당 결합 에너지 면에서 가장 강하게 결합된 핵이다.[13] (니켈-62의 더 높은 결합 에너지가 56Fe보다 더 큰 평균 질량 손실로 이어지지 않는 이유는 62Ni가 철-56보다 중성자/양성자 비율이 약간 더 높으며, 더 무거운 중성자의 존재가 니켈-62의 핵자당 평균 질량을 증가시키기 때문이다).
파괴 에너지를 줄이기 위해 약한 상호작용은 중성자의 수가 양성자의 수를 초과하도록 허용한다. 예를 들어, 철의 주요 동위 원소는 26개의 양성자와 30개의 중성자를 가진다. 중성자의 수가 그 핵자 수에 대해 가장 안정적인 수와 다른 동위 원소도 존재한다. 만약 양성자 하나가 중성자로 바뀌거나 중성자 하나가 양성자로 바뀌는 것이 안정성을 증가시킨다면(질량을 낮춘다면), 이는 베타 붕괴를 통해 일어날 것이며, 이는 핵종이 방사성임을 의미한다.
이러한 변환의 두 가지 방법은 약한 힘에 의해 매개되며, 베타 붕괴의 유형을 포함한다. 가장 간단한 베타 붕괴에서는 중성자가 음전자와 반중성미자를 방출함으로써 양성자로 변환된다. 이는 중성자가 양성자보다 약 2.5개 전자에 해당하는 질량이 더 크기 때문에 핵 외부에서 항상 가능하다. 반대 과정에서는, 핵 내부에서만 발생하며 자유 입자에게는 일어나지 않는데, 양성자가 양전자와 전자 중성미자를 방출함으로써 중성자가 될 수 있다. 이는 모 핵종과 딸 핵종 사이에 충분한 에너지가 있을 경우 허용된다(필요한 에너지 차이는 1.022 MeV로, 전자 2개의 질량과 같다). 만약 모 핵종과 딸 핵종 간의 질량 차이가 이보다 작다면, 양성자가 풍부한 핵은 전자 포획 과정을 통해 양성자를 중성자로 변환할 수 있다. 이 과정에서는 양성자가 원자의 K 궤도 전자를 포획하고 중성미자를 방출하여 중성자가 된다.[11]
가장 무거운 핵들 중, 텔루륨 핵(원소 52)부터 104개 이상의 핵자를 포함하는 핵들은 전기력이 너무 불안정하여 핵의 전체 덩어리가 방출될 수 있다. 보통은 두 개의 양성자와 두 개의 중성자로 구성된 알파 입자로 방출된다(알파 입자는 빠른 헬륨 핵이다).(베릴륨-8도 매우 빠르게 두 개의 알파 입자로 붕괴한다.) 이 유형의 붕괴는 원자량이 104를 넘어갈수록 점점 더 가능성이 커진다.
결합 에너지 곡선은 핵자당 결합 에너지를 원자 질량에 대해 그린 그래프이다. 이 곡선은 철과 니켈에서 주요 봉우리를 보이며 다시 서서히 감소하고, 헬륨에서 좁고 고립된 봉우리를 보이는데, 헬륨은 다른 저질량 핵종보다 더 안정적이다. 자연에서 미량 이상으로 존재하는 가장 무거운 핵인 우라늄 238U는 불안정하지만, 지구의 나이에 가까운 45억 년의 반감기를 가지므로 여전히 상대적으로 풍부하다. 이들(및 헬륨보다 무거운 다른 핵들)은 태양계 형성에 앞서 초신성 폭발과 같은 항성 진화 사건에서 형성되었다. 토륨의 가장 흔한 동위 원소인 232Th도 알파 입자 방출을 겪으며, 그 반감기(원자 수가 절반으로 붕괴하는 시간)는 몇 배 더 길다. 이들 각각에서 방사성 붕괴는 불안정한 딸 동위 원소를 생성하며, 이는 붕괴 사슬을 시작하여 납의 안정된 동위 원소로 끝난다.[11]
핵 결합 에너지 계산
[편집]핵의 핵 결합 에너지를 결정하기 위해 계산을 사용할 수 있다. 이 계산에는 핵 질량 결손을 결정하고, 이를 에너지로 변환하며, 결과를 원자 1몰당 에너지 또는 핵자당 에너지로 표현하는 과정이 포함된다.[1]
핵 질량 결손의 에너지 변환
[편집]핵 질량 결손은 핵 질량과 구성 핵자 및 전자의 질량 합계 사이의 차이로 정의된다. 여기서:
핵 질량 결손은 일반적으로 핵 결합 에너지로 변환된다. 핵 결합 에너지는 핵을 구성 핵자로 분해하는 데 필요한 최소 에너지이다. 이 변환은 질량-에너지 등가: E = ∆mc2를 통해 이루어진다. 그러나 이는 원자 1몰당 에너지 또는 핵자당 에너지로 표현되어야 한다.[1]
핵분열과 핵융합
[편집]핵 에너지는 원자핵이 쪼개지거나(핵분열) 합쳐질 때(핵융합) 방출된다. 핵 질량-에너지가 에너지가 제거될 때 일부 질량을 제거할 수 있는 형태로 변환되는 것은 질량-에너지 등가 공식과 일치한다.
- ΔE = Δm c2,
여기서
- ΔE = 에너지 방출,
- Δm = 질량 결손,
핵 에너지는 1896년 프랑스의 물리학자 앙리 베크렐이 어두운 곳에 보관된 우라늄 근처의 사진 건판이 엑스선 건판처럼 검게 변하는 것을 발견하면서 처음으로 발견되었다(엑스선은 1895년에 최근에 발견되었다).[14]
니켈-62는 어떤 동위 원소보다도 핵자당 결합 에너지가 가장 높다. 핵자당 평균 결합 에너지가 낮은 원자가 핵자당 평균 결합 에너지가 높은 두 개의 원자로 변환되면 에너지가 방출된다. (여기서 평균은 가중 평균이다.) 또한, 평균 결합 에너지가 낮은 두 원자가 융합하여 평균 결합 에너지가 높은 원자를 형성하면 에너지가 방출된다. 그래프는 수소 핵이 융합하여 더 무거운 원자를 형성할 때 에너지가 방출되며, 우라늄이 핵분열하여 더 큰 핵이 더 작은 부분으로 분해될 때도 에너지가 방출된다는 것을 보여준다.
핵 에너지는 세 가지 발열(또는 발열 반응) 과정을 통해 방출된다:
- 방사성 붕괴는 방사성 핵 내의 중성자 또는 양성자가 입자, 전자기파(감마선), 또는 둘 다를 방출하며 자발적으로 붕괴하는 과정이다. 방사성 붕괴의 경우 결합 에너지가 반드시 증가할 필요는 없다는 점에 유의해야 한다. 엄밀히 필요한 것은 질량이 감소하는 것이다. 중성자가 양성자로 변환되고 붕괴 에너지가 중성자와 양성자의 질량 차이에 빛의 속도 제곱을 곱한 값인 0.782343 MeV보다 작다면(루비듐-87이 스트론튬-87로 붕괴하는 것과 같이), 핵자당 평균 결합 에너지는 실제로 감소할 것이다.
- 핵융합은 두 개의 원자핵이 융합하여 더 무거운 핵을 형성한다.
- 핵분열은 무거운 핵이 두 개(또는 드물게 세 개)의 더 가벼운 핵과 일부 중성자로 쪼개지는 것이다.
가벼운 원소의 에너지를 생산하는 핵 상호작용은 약간의 설명이 필요하다. 흔히 모든 가벼운 원소의 에너지 생산 핵 상호작용은 융합으로 분류되지만, 위에서 주어진 정의에 따르면 융합은 생성물이 반응물보다 더 무거운 핵을 포함해야 한다. 가벼운 원소는 융합 또는 핵분열을 통해 에너지를 생산하는 핵 상호작용을 겪을 수 있다. 두 수소 동위 원소 간의 모든 에너지 생산 핵 상호작용과 수소와 헬륨-3 간의 상호작용은 융합이다. 왜냐하면 이러한 상호작용의 생성물에 더 무거운 핵이 포함되기 때문이다. 그러나 중성자와 리튬-6의 에너지 생산 핵 상호작용은 수소-3과 헬륨-4를 생성하는데, 각각 더 가벼운 핵이다. 위 정의에 따르면 이 핵 상호작용은 핵분열이지 융합이 아니다. 이 경우처럼 중성자에 의해 핵분열이 유발될 때, 이를 유도 핵분열이라고 한다.
|
|
원자 결합 에너지
[편집]원자(전자를 포함하여)의 결합 에너지는 원자핵의 결합 에너지와 정확히 같지 않다. 동위 원소의 측정된 질량 결손은 항상 해당 동위 원소의 중성 원자의 질량 결손으로 기록되며, 대부분 MeV/c2 단위로 표시된다. 결과적으로 기록된 질량 결손은 고립된 핵의 안정성이나 결합 에너지 측정이 아니라 전체 원자의 안정성 측정이다. 여기에는 매우 실용적인 이유가 있는데, 즉 무거운 원소를 완전히 이온화하는 것, 즉 모든 전자를 벗겨내는 것이 매우 어렵기 때문이다.
이러한 관행은 다른 이유로도 유용하다. 무거운 불안정한 핵에서 모든 전자를 벗겨내는 것(따라서 맨 핵을 생성하는 것)은 핵의 수명을 변화시키거나, 안정적인 중성 원자의 핵도 벗겨낸 후 불안정해질 수 있는데, 이는 핵이 독립적으로 다루어질 수 없음을 나타낸다. 이러한 예는 GSI 중이온 가속기에서 수행된 구속 상태 β 붕괴 실험에서 나타났다.[15][16] 이는 전자 포획과 같은 현상에서도 명백하다. 이론적으로, 무거운 원자의 원자 궤도 모델에서 전자는 핵 내부를 부분적으로 공전한다(엄밀한 의미에서 공전하는 것이 아니라 핵 내부에 위치할 비영 확률을 가진다).
핵 붕괴는 핵에서 일어나며, 이는 사건에서 핵에 귀속된 특성이 변함을 의미한다. 물리학 분야에서 "결합 에너지"를 측정하는 "질량 결손" 개념은 "중성 원자의 질량 결손"(단순히 핵만이 아님)을 의미하며 전체 원자의 안정성을 측정하는 것이다.
핵 결합 에너지 곡선
[편집]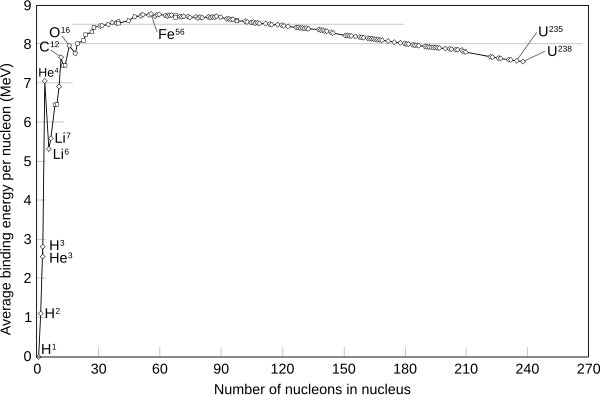
주기율표에서 수소부터 나트륨까지의 가벼운 원소들은 원자 질량이 증가함에 따라 일반적으로 핵자당 결합 에너지가 증가하는 경향을 보인다. 이러한 증가는 핵 내의 핵자당 힘이 증가함에 따라 발생하는데, 각 추가 핵자가 다른 근처 핵자들에게 끌려가므로 전체에 더 강하게 결합되기 때문이다. 헬륨-4와 산소-16은 이러한 경향에 대한 특히 안정적인 예외이다(오른쪽 그림 참조). 이는 이들이 이중 마법수 핵이므로 양성자와 중성자 모두 해당 핵 껍질을 채우기 때문이다.
결합 에너지가 증가하는 영역 다음에는 질량 30에서 질량 90까지의 구간에서 상대적 안정성(포화) 영역이 이어진다. 이 영역에서는 핵이 충분히 커져 핵력이 핵 전체에 효과적으로 미치지 못한다. 이 영역에서 원자 질량이 증가함에 따라 인력적인 핵력은 원자 번호가 증가함에 따라 양성자들 사이의 반발적인 전자기력과 거의 균형을 이룬다.
마지막으로, 더 무거운 원소에서는 원자 번호가 증가함에 따라 핵자당 결합 에너지가 점진적으로 감소한다. 이 핵 크기 영역에서는 전자기적 반발력이 강한 핵력 인력을 압도하기 시작한다.
결합 에너지의 정점에서는 니켈-62가 (핵자당) 가장 강하게 결합된 핵이며, 그 다음은 철-58과 철-56이다.[17] 이것이 철과 니켈이 행성 핵에 매우 흔한 금속인 대략적인 기본적인 이유이다. 이는 초신성과 별의 실리콘 연소 마지막 단계에서 부산물로 풍부하게 생성되기 때문이다. 그러나 정확히 어떤 핵이 생성되는지를 제어하는 것은 (위에서 정의된) 핵자당 결합 에너지가 아니다. 왜냐하면 별 내부에서는 중성자와 양성자가 상호 변환되어 일반 핵자당 훨씬 더 많은 에너지를 방출할 수 있기 때문이다. 실제로, 중성자가 양성자로 베타 붕괴 변환되기 때문에, 극도로 뜨거운 별 핵에서 62Ni의 광붕괴로 56Fe를 형성하는 것이 에너지적으로 가능할 수 있다고 주장되어 왔다.[18] 이것은 핵자당 질량이 가장 낮은 핵종인 56Fe의 생성을 선호한다. 그러나 고온에서는 모든 물질이 최저 에너지 상태에 있지 않을 것이다. 이 에너지 최대값은 또한 T = 298 K 및 p = 1 atm과 같은 주변 조건에서도 유효해야 한다. 그러나 이러한 조건에서 원자의 핵은 가장 안정하고 낮은 에너지 상태의 물질로 융합하는 것이 억제된다.
철이나 니켈처럼 핵자당 결합 에너지가 높은 원소는 핵분열을 겪을 수 없지만, 이론적으로 수소, 중수소, 헬륨, 탄소 등과 융합할 수 있다:[19]
- 62Ni + 12C → 74Se Q = 5.467 MeV
일반적으로 철-56은 메커니즘적인 이유로 우주에서 니켈 동위 원소보다 더 흔하다고 여겨진다. 왜냐하면 불안정한 선조 니켈-56은 초신성 내부에서 14개의 헬륨 핵이 단계적으로 쌓이면서 풍부하게 생성되며, 초신성이 폭발하면서 성간 물질로 방출되기 전에 몇 분 내에 철로 붕괴할 시간이 없기 때문이다. 그러나 니켈-56은 몇 주 내에 코발트-56으로 붕괴하고, 이 방사성 동위 원소는 약 77.3일의 반감기를 가지고 마침내 철-56으로 붕괴한다. 이러한 과정에 의해 구동되는 방사성 붕괴의 광도 곡선은 II형 초신성, 예를 들어 SN 1987A에서 관찰되었다. 별 내부에서는 알파 추가 과정을 통해 니켈-62를 생성하는 좋은 방법이 없으며, 그렇지 않았다면 우주에는 이 고도로 안정적인 핵종이 더 많이 존재했을 것이다.
결합 에너지와 핵종 질량
[편집]최대 결합 에너지가 중간 크기의 핵에서 발견되는 사실은 서로 다른 범위 특성을 가진 두 가지 반대 힘의 상충 효과의 결과이다. 양성자와 중성자를 서로 동일하게 결합하는 인력적인 핵력(강한 핵력)은 거리에 따라 이 힘이 급격히 지수적으로 감소하기 때문에 범위가 제한적이다. 그러나 핵을 분리시키기 위해 양성자들 사이에 작용하는 반발적인 전자기력은 거리에 따라 훨씬 느리게 감소한다(거리의 제곱에 반비례). 지름이 약 4개 이상의 핵자로 구성된 핵의 경우, 추가 양성자의 추가적인 반발력이 추가 강한 힘 상호작용의 결과로 추가된 핵자들 사이에서 발생하는 결합 에너지를 상쇄한다. 이러한 핵은 크기가 증가함에 따라 점점 더 약하게 결합되지만, 대부분은 여전히 안정하다. 마지막으로, 209개 이상의 핵자(지름이 약 6개 이상의 핵자)를 포함하는 핵은 모두 너무 커서 안정하지 못하며, 더 작은 핵으로 자발적인 붕괴를 겪는다.
핵융합은 가장 가벼운 원소들을 더 강하게 결합된 원소(예: 수소를 헬륨으로)로 결합하여 에너지를 생산하고, 핵분열은 가장 무거운 원소(예: 우라늄과 플루토늄)를 더 강하게 결합된 원소(예: 바륨과 크립톤)로 분할하여 에너지를 생산한다. 몇몇 가벼운 원소(리튬 등)의 핵분열은 헬륨-4가 생성물이며 약간 더 무거운 원소들보다 더 강하게 결합된 원소이기 때문에 발생한다. 두 과정 모두 생성물의 질량 합이 반응하는 핵의 질량 합보다 작기 때문에 에너지를 생산한다.
위에서 중수소의 예에서 보듯이, 핵 결합 에너지는 질량과 에너지의 등가성에 따라 분수적인 질량 결손으로 쉽게 측정될 수 있을 만큼 충분히 크다. 원자 결합 에너지는 단순히 자유 핵자들의 집합이 원자핵을 형성하기 위해 결합될 때 방출되는 에너지(및 질량)의 양이다.
핵 결합 에너지는 핵의 질량과 핵을 구성하는 자유 중성자 및 양성자의 질량 합계의 차이로부터 계산할 수 있다. 이 질량 차이, 즉 질량 결손 또는 질량 부족이 알려지면, 아인슈타인의 질량-에너지 등가 공식 E = mc2를 사용하여 모든 핵의 결합 에너지를 계산할 수 있다. 초기 핵 물리학자들은 이 값을 "충전 분율" 계산이라고 불렀다.
예를 들어, 달튼(1 Da)은 12C 원자 질량의 1/12로 정의되지만, 1H 원자(양성자 + 전자)의 원자 질량은 1.007825 Da이므로, 12C의 각 핵자는 평균적으로 질량의 약 0.8%를 결합 에너지 형태로 잃었다.
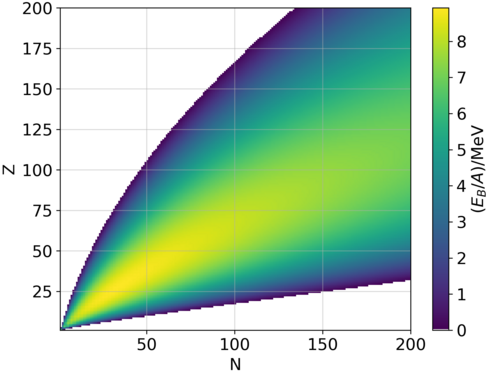
핵 결합 에너지에 대한 반경험적 공식
[편집]Z개의 양성자와 N개의 중성자를 포함하여 총 A개의 핵자를 가진 핵에 대한 핵자당 결합 에너지(EB)의 반경험적 질량 공식은 다음과 같다. 여기서 계수는 다음과 같다: ; ; ; ; .
첫 번째 항 는 포화 기여라고 불리며, 핵자당 결합 에너지가 모든 핵에 대해 일차 근사적으로 동일하도록 보장한다. 항은 표면 장력 효과이며, 핵 표면에 위치한 핵자 수에 비례한다. 이는 가벼운 핵에서 가장 크다. 항은 쿨롱 정전기 반발력이며, 가 증가할수록 중요해진다. 대칭 보정 항 는 다른 효과가 없을 때 가장 안정적인 배열이 양성자와 중성자의 수가 같다는 사실을 고려한다. 이는 핵 내의 중성자-양성자 상호작용이 중성자-중성자 또는 양성자-양성자 상호작용보다 강하기 때문이다. 짝짓기 항 는 순수하게 경험적이다. 이는 짝수-짝수 핵의 경우 +이고, 홀수-홀수 핵의 경우 –이다. A가 홀수일 때 짝짓기 항은 동일하게 0이다.
실험적으로 측정된 원자 핵종 질량에서 도출된 예시 값
[편집]다음 표는 일부 결합 에너지와 질량 결손 값을 나열한다.[20] 또한 1 Da = 931.494028(23) MeV/c2임을 유의한다. 결합 에너지를 계산하기 위해 Z (mp + me) + N mn − mnuclide 공식을 사용하는데, 여기서 Z는 핵종의 양성자 수를, N은 중성자 수를 나타낸다. 우리는 mp = 938.2720813(58) MeV/c2, me = 0.5109989461(30) MeV/c2 및 mn = 939.5654133(58) MeV/c2를 사용한다. 문자 A는 Z와 N의 합(핵종의 핵자 수)을 나타낸다. 만약 우리가 기준 핵자가 중성자의 질량을 가진다고 가정한다면(그리하여 계산된 모든 "총" 결합 에너지는 최대가 된다), 우리는 총 결합 에너지를 핵의 질량과 A개의 자유 중성자 집합의 질량의 차이로 정의할 수 있다. 다시 말해, 이는 (Z + N) mn − mnuclide가 될 것이다. "핵자당 총 결합 에너지"는 이 값을 A로 나눈 값이 될 것이다.
| 핵종 | Z | N | 질량 초과 | 총 질량 | 총 질량 / A | 핵자당 총 결합 에너지 | 질량 결손 | 결합 에너지 | 핵자당 결합 에너지 |
|---|---|---|---|---|---|---|---|---|---|
| 56Fe | 26 | 30 | −60.6054 MeV | 55.934937 Da | 0.9988372 Da | 9.1538 MeV | 0.528479 Da | 492.275 MeV | 8.7906 MeV |
| 58Fe | 26 | 32 | −62.1534 MeV | 57.932276 Da | 0.9988496 Da | 9.1432 MeV | 0.547471 Da | 509.966 MeV | 8.7925 MeV |
| 60Ni | 28 | 32 | −64.472 MeV | 59.93079 Da | 0.9988464 Da | 9.1462 MeV | 0.565612 Da | 526.864 MeV | 8.7811 MeV |
| 62Ni | 28 | 34 | −66.7461 MeV | 61.928345 Da | 0.9988443 Da | 9.1481 MeV | 0.585383 Da | 545.281 MeV | 8.7948 MeV |
56Fe는 이 표에 나열된 네 가지 핵종 중 핵자당 질량이 가장 낮지만, 이것이 핵자당 가장 강하게 결합된 원자임을 의미하지는 않는다. 시작 핵자 선택이 완전히 자유롭지 않는 한 말이다. 철은 56개의 핵자가 핵종을 형성하도록 허용될 경우(필요하다면 서로 변환될 수 있음) 가장 많은 에너지를 방출한다. 핵종과 동일한 수의 양성자 Z와 총 핵자 A로 시작하는 핵자당 가장 높은 결합 에너지는 62Ni이다. 따라서 핵의 총 결합 에너지의 진정한 절대값은 핵을 무엇으로 구성할 수 있는지에 따라 달라진다. 만약 질량수 A를 가진 모든 핵이 A개의 중성자로 구성될 수 있다고 가정한다면, 56Fe는 62Ni보다 양성자 비율이 높기 때문에 핵자당 가장 많은 에너지를 방출할 것이다. 그러나 핵이 핵이 포함하는 것과 동일한 수의 양성자와 중성자로만 구성되어야 한다면, 니켈-62가 핵자당 가장 강하게 결합된 핵이다.
| 핵종 | Z | N | 질량 초과 | 총 질량 | 총 질량 / A | 핵자당 총 결합 에너지 | 질량 결손 | 결합 에너지 | 핵자당 결합 에너지 |
|---|---|---|---|---|---|---|---|---|---|
| n | 0 | 1 | 8.0716 MeV | 1.008665 Da | 1.008665 Da | 0.0000 MeV | 0 Da | 0 MeV | 0 MeV |
| 1H | 1 | 0 | 7.2890 MeV | 1.007825 Da | 1.007825 Da | 0.7826 MeV | 0.0000000146 Da | 0.0000136 MeV | 13.6 eV |
| 2H | 1 | 1 | 13.13572 MeV | 2.014102 Da | 1.007051 Da | 1.50346 MeV | 0.002388 Da | 2.22452 MeV | 1.11226 MeV |
| 3H | 1 | 2 | 14.9498 MeV | 3.016049 Da | 1.005350 Da | 3.08815 MeV | 0.0091058 Da | 8.4820 MeV | 2.8273 MeV |
| 3He | 2 | 1 | 14.9312 MeV | 3.016029 Da | 1.005343 Da | 3.09433 MeV | 0.0082857 Da | 7.7181 MeV | 2.5727 MeV |
위 표에서 중성자의 붕괴와 삼중수소의 헬륨-3로의 변환은 에너지를 방출한다는 것을 알 수 있다. 따라서 이는 동일한 수의 중성자의 질량과 비교했을 때 더 강하게 결합된 새로운 상태를 나타내며(또한 총 핵자 수당 더 가벼운 상태를 나타낸다). 이러한 반응은 이전에 고정된 중성자와 양성자의 N 및 Z 수에서 계산된 결합 에너지의 변화에 의해 유도되는 것이 아니라 반응과 함께 핵종의 총 질량/핵자당 질량 감소에 의해 유도된다. (수소-1에 대해 위에 주어진 결합 에너지는 원자 결합 에너지이며, 0이 될 핵 결합 에너지는 아님을 유의한다.)
같이 보기
[편집]- 중력 결합 에너지
- 결합 해리 에너지: 화학 결합 내 원자들 사이의 결합 에너지
- 전자 결합 에너지: 원자 궤도 또는 고체에서 전자를 자유롭게 하는 데 필요한 에너지
- 원자 결합 에너지: 원자를 자유 전자와 핵으로 분해하는 데 필요한 에너지
- 양자색역학 결합 에너지: 하드론 내부에서 다양한 쿼크를 서로 결합시키는 부분의 질량과 운동 에너지를 다룸
각주
[편집]- ↑ 가 나 다 “Nuclear binding energy”. 《How to solve for nuclear binding energy. Guides to solving many of the types of quantitative problems found in Chemistry 116.》. Purdue University. July 2010. 2010년 7월 10일에 확인함.
- ↑ Nave, Rod (July 2010). “Nuclear Binding Energy”. 《Hyperphysics – a free web resource from GSU》. Georgia State University. 2010년 7월 11일에 확인함.
- ↑ “Nuclear Energy”. 《Energy Education is an interactive curriculum supplement for secondary-school science students, funded by the U. S. Department of Energy and the Texas State Energy Conservation Office (SECO)》. U. S. Department of Energy and the Texas State Energy Conservation Office (SECO). July 2010. 2011년 2월 26일에 원본 문서에서 보존된 문서. 2010년 7월 10일에 확인함.
- ↑ 가 나 Stern, Dr. David P. (2004년 9월 23일). “Nuclear Physics”. 《"From Stargazers to Starships" Public domain content.》. NASA website. 2010년 7월 11일에 확인함.
- ↑ 가 나 다 라 마 바 Stern, Dr. David P. (2004년 11월 15일). “A Review of Nuclear Structure”. 《"From Stargazers to Starships" Public domain content.》. NASA website. 2010년 7월 11일에 확인함.
- ↑ “It's Elemental – The Element Helium”. 《education.jlab.org》. 2019년 11월 5일에 확인함.
- ↑ Frisch, David H.; Thorndike, Alan M. (1964). 《Elementary Particles》. Princeton, New Jersey: David Van Nostrand. 11–12쪽.
- ↑ “20.8: Converting Mass to Energy: Mass Defect and Nuclear Binding Energy”. 《Chemistry LibreTexts》 (영어). 2016년 3월 11일. 2019년 11월 5일에 확인함.
- ↑ Pourshahian, Soheil (2017년 9월 1일). 《Mass Defect from Nuclear Physics to Mass Spectral Analysis》. 《Journal of the American Society for Mass Spectrometry》 (영어) 28. 1836–1843쪽. Bibcode:2017JASMS..28.1836P. doi:10.1007/s13361-017-1741-9. ISSN 1879-1123. PMID 28733967. S2CID 34178643.
- ↑ “On the Interaction of Natural Forces” (미국 영어). New York, Appleton. 1854. 2022년 12월 24일에 확인함.
- ↑ 가 나 다 라 마 바 사 아 자 차 Stern, Dr. David P. (2009년 2월 11일). “Nuclear Binding Energy”. 《"From Stargazers to Starships" Public domain content》. NASA website. 2010년 7월 11일에 확인함.
- ↑ 방출되는 에너지는 헬륨의 결합 에너지보다 약간 적은데, 이는 시작점이 두 개의 양성자와 두 개의 중성자가 아니라 네 개의 양성자이기 때문이다.
- ↑ N R Sree Harsha, "The tightly bound nuclei in the liquid drop model", Eur. J. Phys. 39 035802 (2018), doi:10.1088/1361-6404/aaa345
- ↑ “Marie Curie – X-rays and Uranium Rays”. aip.org. 2006년 4월 10일에 확인함.
- ↑ Jung, M.; 외. (1992). 《First observation of bound-state β− decay》. 《피지컬 리뷰 레터》 69. 2164–2167쪽. Bibcode:1992PhRvL..69.2164J. doi:10.1103/PhysRevLett.69.2164. PMID 10046415.
- ↑ Bosch, F.; 외. (1996). 《Observation of bound-state beta minus decay of fully ionized 187Re: 187Re–187Os Cosmochronometry》. 《피지컬 리뷰 레터》 77. 5190–5193쪽. Bibcode:1996PhRvL..77.5190B. doi:10.1103/PhysRevLett.77.5190. PMID 10062738.
- ↑ Fewell, M. P. (1995). 《The atomic nuclide with the highest mean binding energy》. 《American Journal of Physics》 63. 653–658쪽. Bibcode:1995AmJPh..63..653F. doi:10.1119/1.17828.
- ↑ M.P. Fewell, 1995
- ↑ From the difference of binding energy, 5.467 = 642.891 − 545.262 − 92.162, values from "Mass number, number of protons, name of isotope, mass [MeV/c^2], binding energy [MeV] and binding energy per nucleus [MeV] for different atomic nuclei" at Einstein Online, Max Planck Institute for Gravitational Physics.
- ↑ Jagdish K. Tuli, Nuclear Wallet Cards, 7th edition, April 2005, Brookhaven National Laboratory, US National Nuclear Data Center
외부 링크
[편집] 위키미디어 공용에 핵 결합 에너지 관련 미디어 분류가 있습니다.
위키미디어 공용에 핵 결합 에너지 관련 미디어 분류가 있습니다.













