前推 (微分)

假设 $\phi :M\rightarrow N$ 是光滑流形之间的光滑映射；则 $\phi$ 在一点 $x$ 处的微分在某种意义上是 $\phi$ 在 $x$ 附近的最佳线性逼近。这可以视为通常微积分中全导数的推广。确切地说，它是从 $M$ 在 $x$ 处的切空间到 $N$ 在 $\phi (x)$ 处的切空间的一个线性映射，从而可以将 $M$ 的切向量“前推”成 $N$ 的切向量。

映射 $\phi$ 的微分也被一些的作者称为 $\phi$ 的导数或全导数，有时它自己也之称为前推（pushforward）。

动机

设 $\phi :U\rightarrow V$ 是从 $\mathbb {R} ^{m}$ 的一个开集 $U$ 到 $\mathbb {R} ^{n}$ 的开集 $V$ 的一个光滑映射。对任何 $U$ 中的给定点 $x$ ， $\phi$ 在 $x$ 的雅可比矩阵（关于标准坐标）是 $\phi$ 在 $x$ 的全微分的矩阵表示，这是一个从 $\mathbb {R} ^{m}$ 到 $\mathbb {R} ^{n}$ 的线性映射：

\mathrm {d} \varphi _{x}:\mathbb {R} ^{m}\to \mathbb {R} ^{n}\ .

我们希望将其推广到 $\phi$ 是“任何”两个光滑流形 $M$ 与 $N$ 之间的光滑映射。

光滑映射的微分

令 $\phi :M\rightarrow N$ 是光滑流形间的光滑映射。给定某点 $x\in M$ ， $\phi$ 在 $x$ 的微分或（全）导数是从 $M$ 在 $x$ 的切空间到 $N$ 在 $\phi (x)$ 的切空间一个线性映射

\mathrm {d} \varphi _{x}:T_{x}M\to T_{\varphi (x)}N\ ,

映射 $\operatorname {d} \!\phi _{x}$ 运用到切向量 $X$ 上有时称为 $X$ 由 $\phi$ 的前推。前推的确切定义取决于我们怎样定义切向量（不同的定义可参见切空间）。

如果我们定义切向量为通过 $x$ 的曲线等价类，那么微分由

\mathrm {d} \varphi _{x}(\gamma '(0))=(\varphi \circ \gamma )'(0)

给出，这里 $\gamma$ 是 $M$ 上满足 $\gamma (0)=x$ 的一条曲线。换句话说，一条曲线 $\gamma$ 在 0 处切向量的前推恰好是 $\phi \circ \gamma$ 在 0 处的切向量。

另一种方式，如果切向量定义为作用在光滑实值函数上的导子，那么微分由

\mathrm {d} \varphi _{x}(X)(f)=X(f\circ \varphi )

给出，这里 $X\in T_{x}M$ ，从而 $X$ 是定义在 $M$ 上的一个导子而 $f$ 是 $N$ 上一个光滑实值函数。根据定义，在给定 $M$ 上 $x$ 处 $X$ 的前推在 $T_{\phi (x)}N$ 中，从而定义了一个 $N$ 上的导子。

取定 $x$ 与 $\phi (x)$ 附近的坐标卡以后， $F$ 局部由 $\mathbb {R} ^{m}$ 与 $\mathbb {R} ^{n}$ 之间的光滑映射

{\hat {\varphi }}:U\rightarrow V

确定。而 $\operatorname {d} \!\phi _{x}$ 具有表示（在 $x$ 附近）：

\mathrm {d} \varphi _{x}{\Bigl (}{\frac {\partial }{\partial u^{a}}}{\Bigr )}={\frac {\partial {\hat {\varphi }}^{b}}{\partial u^{a}}}{\frac {\partial }{\partial v^{b}}},

这里使用了爱因斯坦求和约定，偏导数对 $x$ 坐标卡相应的 $U$ 中的点取值。

线性扩张得到如下矩阵

(\mathrm {d} \varphi _{x})_{a}^{\;b}={\frac {\partial {\hat {\varphi }}^{b}}{\partial u^{a}}}.

从而光滑映射 $\phi$ 在每一点的微分是切空间之间的一个线性变换。从而在某些选定的局部坐标下，它表示为相应的从 $\mathbb {R} ^{m}$ 到 $\mathbb {R} ^{n}$ 光滑映射的雅可比矩阵。一般情形，微分不要求可逆。如果 $\phi$ 是一个局部微分同胚，那么在 $x$ 点的前推是可逆的，其逆给出 $T_{\phi (x)}N$ 的拉回。

另外，局部微分同胚的微分是切空间之间的线性同构。

微分经常有其他一些记法，比如

D\varphi _{x},\;(\varphi _{*})_{x},\;\varphi '(x)\ .

从定义可得出复合函数的微分便是微分的复合（即，具有函子性质），这便是光滑函数微分的链式法则。

切丛上的微分

光滑映射 $\phi$ 的微分以显而易见的方式诱导了从 $M$ 的切丛到 $N$ 的切丛的一个丛映射（事实上是向量丛同态），记为 $\operatorname {d} \!\phi$ 或 $\phi *$ ，满足如下的交换图表：

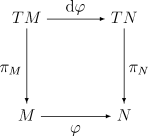
这里 $\pi _{M}$ 与 $\pi _{N}$ 分别表示 $M$ 与 $N$ 切丛的丛投影。

等价地（参见丛映射）， $\phi *=\operatorname {d} \!\phi$ 是从 $TM$ 到 $M$ 上的拉回丛 $\phi ^{*}TN$ 的丛映射，这可以看成 $M$ 上向量丛 $\hom(TM,\phi ^{*}TN)$ 的一个截面。

向量场的前推

给定了一个光滑映射 $\phi :M\rightarrow N$ 与 $M$ 上一个向量场 $X$ ，一般不能定义 $X$ 通过 $\phi$ 的前推为 $N$ 的一个向量场。譬如，如果映射 $\phi$ 不是满射，则在 $\phi$ 的像外部没有自然的方式定义拉回；如果 $\phi$ 不是单射也有可能在给定一点拉回不止一种选择。无论如何，可以用“沿着映射的向量场”概念将难处变精确。

$M$ 上 $\phi ^{*}TN$ 的一个截面称为沿着 $\phi$ 的向量场。例如，如果 $M$ 是 $N$ 的一个子丛而 $\phi$ 是包含映射，那么沿着 $\phi$ 的向量场恰好是 $N$ 沿着 $M$ 的切丛的一个截面；特别的， $M$ 上的向量通过 $TM$ 包含到 $TN$ 中定义这样一个截面。这种想法推广到任何光滑映射。

假设 $X$ 是 $M$ 上一个向量场，即 $TM$ 的一个截面。那么，运用逐点微分得出 $X$ 的前推 $\phi ^{*}X$ ，这是一个沿着 $\phi$ 的向量场，即 $M$ 上 $\phi ^{*}TN$ 的一个截面。

任何 $N$ 上的向量场 $Y$ 定义了 $\phi ^{*}TN$ 的一个拉回截面 $\phi ^{*}Y$ 使得 $(\phi ^{*}Y)_{X}=Y_{\phi (x)}$ 。 $M$ 上一个向量场 $X$ 与 $N$ 上一个向量场 $Y$ 称为 $\phi$ -相关的，如果作为沿着 $\phi$ 的向量场有 $\phi *X=\phi ^{*}Y$ 。换句话说，对任何 $x$ 属于 $M$ ，有 $\operatorname {d} \!\phi _{x}(X)=Y_{\phi (x)}$ 。

在某些情形，给定 $M$ 上一个向量场 $X$ ， $N$ 上只有惟一的向量场 $Y$ 与 $X\phi$ -相关。特别地，这在 $\phi$ 是微分同胚时自然成立。在这种情况下，前推定义了 $N$ 上一个向量场 $Y$ ，由

Y_{x}=\varphi _{*}(X_{\varphi ^{-1}(x)}).

给出。一个更一般的情形是 $\phi$ 为满射（比如纤维丛的丛投影）。这时 $M$ 上的向量场 $X$ 称为可投影的，如果对任何 $y$ 属于 $N$ , $\operatorname {d} \!\phi _{x}(X_{x})$ 与 $x$ 属于 $\phi ^{-1}(\{y\})$ 的取法无关。这恰好是保证 $X$ 的前推可以作为 $N$ 上的一个良定的向量场的条件。

參閲

拉回

参考文献

John M. Lee, Introduction to Smooth Manifolds, (2003) Springer Graduate Texts in Mathematics 218.
Jurgen Jost, Riemannian Geometry and Geometric Analysis, (2002) Springer-Verlag, Berlin ISBN 3-540-42627-2 See section 1.6.
Ralph Abraham and Jerrold E. Marsden, Foundations of Mechanics, (1978) Benjamin-Cummings, London ISBN 0-8053-0102-X See section 1.7 and 2.3.