Усечённая четырёх-пятиугольная мозаика

Усечённая четырёх-пятиугольная мозаика
Тип	Гиперболическая однородная мозаика
Конфигурация вершины	4.8.10
Символ Шлефли	t{5,4} или $t{\begin{Bmatrix}5\\4\end{Bmatrix}}$
Символ Витхоффа	2 5 4 |
Симметрии	[5,4], (*542)
Диаграммы Коксетера — Дынкина	или
Двойственные соты	кис-ромбическая мозаика порядка 4-5
Свойства	Изогональная

Усечённая четырёх-шестиугольная мозаика — это a полурегулярная мозаика на гиперболической плоскости. Мозаика имеет символ Шлефли t_0,1,2{4,5} or tr{4,5}.

Симметрия

Усечённая четырёх-пятиугольная мозаика Truncated с линиями зеркал.

Имеется четыре подгруппы с малым индексом, построенных из [5,4] путём удаления зеркал и операцией альтернации. На рисунках фундаментальные области показаны разными цветами, а зеркала находятся на границах областей разного цвета.

Радикальная подгруппа [5*,4] (индекс 10) строится как [5⁺,4], (5*2) с удалением точек вращения, что превращает её в орбифолд (*22222), а её прямая подгруппа [5*,4]⁺ (индекс 20) становится орбифолдом (22222).

Подгруппы [5,4] с малым индексом
Индекс	1	2		10
Диаграмма
[Коксетер] (Орбифолд)	[5,4] = (*542)	[5,4,1+] = = (*552)	[5+,4] = (5*2)	[5*,4] = (*222222)
Прямые подгруппы
Индекс	2	4		20
Диаграмма
Коксетер (орбифолд)	[5,4]+ = (542)	[5+,4]+ = = (552)		[5*,4]+ = (22222)

Связанные многогранники и мозаики

*n42 симметрии общеусечённых мозаик: 4.8.2n

Симметрия *n42 [n,4]	Сферическая		Евклидова	Компактная гиперболическая				Паракомп.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]…	*∞42 [∞,4]
Общеусечённая фигура	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Общеусечённые двойственные	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

*nn2 мутации симметрий всеусечённых мозаик: 4.2n.2n
Симметрия *nn2 [n,n]	Сферическая		Евклидова	Компактная гиперболическая				Паракомпактная
	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Рисунок
Конф.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Двойственная фигура
Конф.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

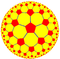
Однородные пятиугольные/квадратные мозаики
Симметрия: [5,4], (*542)							[5,4]+, (542)	[5+,4], (5*2)	[5,4,1+], (*552)
{5,4}	t{5,4}	r{5,4}	2t{5,4}=t{4,5}	2r{5,4}={4,5}	rr{5,4}	tr{5,4}	sr{5,4}	s{5,4}	h{4,5}
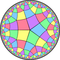
Однородные двойственные
V54	V4.10.10	V4.5.4.5	V5.8.8	V45	V4.4.5.4	V4.8.10	V3.3.4.3.5	V3.3.5.3.5	V55

См. также

• Однородные мозаики на гиперболической плоскости
• Список правильных многомерных многогранников и соединений

Ссылки

• Weisstein, Eric W. Hyperbolic tiling (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Poincaré hyperbolic disk (англ.) на сайте Wolfram MathWorld.
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch