Плосконосая четырёхвосьмиугольная мозаика

Плосконосая четырёхвосьмиугольная мозаика
Тип	Однородная гиперболическая мозаика
Конфигурация вершины	3.3.4.3.8
Символ Шлефли	sr{8,4} или $s{\begin{Bmatrix}8\\4\end{Bmatrix}}$
Символ Витхоффа	| 8 4 2
Симметрии	[8,4]+, (842)
Диаграммы Коксетера — Дынкина
Двойственные соты	Цветочная пятиугольная мозаика порядка 8-4
Свойства	изогональная, хиральная

Плосконосая четырёхвосьмиугольная мозаика — это однородная мозаика на гиперболической плоскости. Её символ Шлефли sr{5,4}.

Изображения

Рисунок в виде хиральной пары, рёбра между чёрными треугольниками не нарисованы:

Связанные многогранники и мозаики

Плосконосая четырёхвосьмиугольная мозаика является седьмой в ряду плосконосых многогранников и мозаик с конфигурацией вершины 3.3.4.3.n.

4n2 симметрии плосконосых мозаик: 3.3.4.3.n
Симметрия 4n2	Сферическая		Евклидова	Компактная гиперболическая				Paracomp.
	242	342	442	542	642	742	842	∞42
Плосконосые мозаики
Конфиг.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Гиро- мозаики
Конфиг.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

Однородные восьмиугольные/квадратные мозаики
[8,4], (*842) (with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries) (и подсимметрия [(∞,4,∞,4)] (*4242) )
= = =	=	= = =	=	= =	=
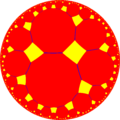
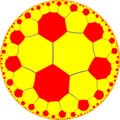
{8,4}	t{8,4}	r{8,4}	2t{8,4}=t{4,8}	2r{8,4}={4,8}	rr{8,4}	tr{8,4}
Однордные двойственные
V84	V4.16.16	V(4.8)2	V8.8.8	V48	V4.4.4.8	V4.8.16
Альтернированные
[1+,8,4] (*444)	[8+,4] (8*2)	[8,1+,4] (*4222)	[8,4+] (4*4)	[8,4,1+] (*882)	[(8,4,2+)] (2*42)	[8,4]+ (842)
=	=	=	=	=	=
h{8,4}	s{8,4}	hr{8,4}	s{4,8}	h{4,8}	hrr{8,4}	sr{8,4}
Альтернированные двойственные
V(4.4)4	V3.(3.8)2	V(4.4.4)2	V(3.4)3	V88	V4.44	V3.3.4.3.8

Смотрите также

• Квадратная мзаика
• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Список однородных мозаик на евклидовой плоскости
• Список правильных многомерных многогранников и соединений

Ссылки

• Weisstein, Eric W. Hyperbolic tiling (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Poincaré hyperbolic disk (англ.) на сайте Wolfram MathWorld.
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch