Усечённая треугольно-шестиугольная мозаика

Усечённая треугольно-шестиугольная мозаика

Тип	Полуправильная мозаика
Конфигурация вершины	4.6.12
Символ Шлефли	tr{6,3} или $t{\begin{Bmatrix}6\\3\end{Bmatrix}}$
Символ Витхоффа	2 6 3 \|
Симметрии	p6, [6,3]⁺, (632)
Диаграммы Коксетера — Дынкина
Двойственная мозаика	Кисромбическая мозаика
Акроним Бауэрса	Othat
Свойства	изогональная

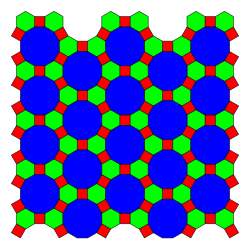
Усечённая треугольно-шестиугольная мозаика — это одна из восьми однородных мозаик на евклидовой плоскости. Мозаика имеет один квадрат, один шестиугольник и один двенадцатиугольник в каждой вершине. Её символ Шлефли tr{3,6}.

Имена

Название усечённая треугольно-шестиугольная мозаика аналогично названиям Усечённый кубооктаэдр и Ромбоусечённый икосододекаэдр, но в некотором смысле вводит в заблуждение.

Настоящее усечение тришестиугольной мозаики имеет прямоугольники, а не квадраты, а его шестиугольные и двенадцатиугольные грани не могут одновременно быть правильными.

Альтернативными взаимозаменяемыми названиями являются:

Большая ромбитришестиугольная мозаика
Ромбоусечённая треугольно-шестиугольная мозаика
Всеусечённая шестиугольная мозаика, всеусечённая треугольная мозаика
Конвей назвал её truncated hexadeltille (усечённый шестипаркет)^[1].

Тришестиугольная мозаика и её усечение

Однородная раскраскаs

Существует только одна однородная раскраска усечённой треугольно-шестиугольной мозаики. 2-Однородная раскраска имеет два цвета шестиугольников. 3-Однородная раскраска может иметь 3 цвета двенадцатиугольников и 3 цвета квадратов.

	1-однородная	2-однородная	3-однородная
Раскраска
Симметрия	p6m, [6,3], (*632)	p3m1, [3^[3]], (*333)

Свазанные 2-однородные мозаики

Усечённая треугольно-шестиугольная мозаика имеет три связанные 2-однородные мозаики^[англ.], одной из которых является 2-однородная раскраска полуправильной ромбитришестиугольной мозаики. Первая мозаика разбивает шестиугольники на 6 треугольников. Другие два разбивает двенадцатиугольники на центральный шестиугольник и окружающие его на треугольники и квадраты в двух различных ориентациях^[2]^[3].

Полуправильные	Разбиения	Полуправильные	2-однородные		3-однородные

Двойственные	Вставки

Упаковка кругов

Усечённая треугольно-шестиугольная мозаика может быть использована для упаковка кругов, если разместить круги одинакового диаметра с ценрами в каждой точке. Тогда каждый круг соприкасается с 3 другими окружностями в упаковке (контактное число)^[4].

Разделенная ромбическая мозаика

Разделенная ромбическая мозаика

Тип	Двойственная полуправильной мозаике
Конфигурация грани	V4.6.12 3.3.3.4.4
Символ Шлефли	{3,6}:e s{∞}h₁{∞}
Символ Витхоффа	2 \| 2 (2 2)
Группа обоев	p6m, [6,3], (*632)
Группа вращений	p6, [6,3]⁺, (632)
Диаграммы Коксетера — Дынкина
Двойственная мозаика	усечённая треугольно-шестиугольная мозаика
Свойства	гранетранзитивная

Разделенная ромбическая мозаика или 3-6 разделенная ромбическая мозаика — это мозаика на евклидовой плоскости. Мозаика строится конгруэнтными треугольниками 30-60-90 с 4, 6 и 12 треугольниками в каждой вершине.

Разделение граней этих мозаик создаёт разделенную ромбическую мозаику.

3-6 дельтоидальная
ромбическая
шестиугольная
шестиугольная
треугольная
треугольная
(как шестиразделённая шестиугольная)
триразделённая треугольная^[англ.]

Разделенная ромбическая мозаика под двойственной ей (слева) и под цветочной пятиугольной мозаикой (справа),

из которой она может быть создана как частичное усечение.

Построение из ромбической мозаики

Конвей называет её kisrhombille^[5] (kis означает операцию деления, применённой здесь к ромбической мозаике). Более точно можно назвать её 3-6 разделённой ромбической мозаикой, чтобы отличить её от других похожих гиперболических мозаик, наподобие 3-7 разделённой ромбической мозаики^[англ.].

Мозаику можно рассматривать как равностороннюю шестиугольную мозаику с каждым шестиугольником, разделённым на 12 треугольников из центральной точки. (Альтернативно мозаику можно рассматривать как разделённую треугольную мозаику, разделённую на 6 треугольников, или как бесконечная конфигурация прямых из шести параллельных семейств.)

Мозаика обозначена как V4.6.12, поскольку каждая треугольная грань имеет три типа вершин - одна с 4, одна с 6 и одна с 12 треугольниками.

Симметрия

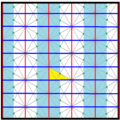
Треугольники разделенной ромбической мозаика представляют фундаментальные области p6m, [6,3] (*632 Орбифолдная нотация^[англ.]) симметрии группы обоев. Есть ряд подгрупп с малым индексом, построенных из [6,3] путём удаления зеркал и альтернации. [1⁺,6,3] образует симметрию *333, показанную как красные линии зеркал. [6,3⁺] создаёт симметрию 3*3. [6,3]⁺ является подгруппой вращений. Коммутатором является [1⁺,6,3⁺], который имеет симметрию 333. Подгруппа с индексом 6, построенная как [6,3*], также становится (*333), показанной как синие линии зеркал, и она имеет собственную вращательную симметрию 333 с индексом 12.

Подгруппы с малым индексом [6,3] (*632)
Индекс	1	2		3	6
Диаграмма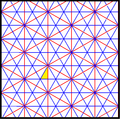
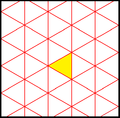
Межд.(орб.) (орб.) Коксетер	p6m (*632) [6,3] = =	p3m1 (*333) [1⁺,6,3] = =	p31m (3*3) [6,3⁺] =	cmm (2*22)	pmm (*2222)	p3m1 (333) [6,3] = =
Прямые подгруппы
Индекс	2	4		6	12
Диаграмма
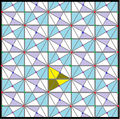
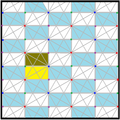
Межд.(орб.) Коксетер	p6 (632) [6,3]⁺ = =	p3 (333) [1⁺,6,3⁺] = =		p2 (2222)	p2 (2222)	p3 (333) [1⁺,6,3*] = =
Замечание: Операция ⁺ в нотации Коксетера заменяет отражения вращениями. Когда данная операция применяется к группе Коксетера, подгруппа называется прямой подгруппой, поскольку остаются лишь прямые изометрии без отражений.

Связанные многогранники и шаблоны

Существует восемь однородных мозаик, которые могут быть основаны на правильной шестиугольной мозаике (или двойственной треугольной мозаике). Если рисовать плитки красными на месте исходных граней, жёлтым на месте исходных вершин и синим вдоль исходных рёбер, существует 8 форм, 7 из которых топологически различны. (Усечённая треугольная мозаика топологически идентична шестиугольной мозаике.)

Однородные шестиугольные/треугольные мозаики
Симметрия: [6,3], (*632)							[6,3]⁺ (632)	[6,3⁺] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}


6³	3.12²^[англ.]	(3.6)²	6.6.6	3⁶	3.4.12.4	4.6.12^[англ.]	3.3.3.3.6	3.3.3.3.3.3
Двойственные им однородные мозаики

V6³	V3.12²^[англ.]	V(3.6)²	V6³	V3⁶	V3.4.12.4	V.4.6.12^[англ.]	V3⁴.6	V3⁶

Варианты симметрии

Эта мозаика может считаться членом последовательности однородных мозаик с вершинной фигурой (4.6.2p) и диаграммой Коксетера — Дынкина . Для p < 6 членами последовательности являются всеусечённые^[англ.] многогранники (зоноэдры), которые показаны ниже как сферические мозаики. Для p > 6 мозаики являются гиперболическими, начиная с усечённой треугольно-семиугольной мозаики^?!.

*n32 мутации по симметрии полностью усечённых мозаик: *4.6.2n*
Симметрия *n32^[англ.] n,3^[англ.]	Сферическая				Евклидова	Компактная гиперболическая		Паракомп.	Некомпактная гиперболическая
Симметрия *n32^[англ.] n,3^[англ.]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Фигуры
Конфигурация	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Двойственная
Конфигурация грани	V4.6.4^[англ.]	V4.6.6	V4.6.8^[англ.]	V4.6.10	V4.6.12^[англ.]	V4.6.14^[англ.]	V4.6.16^[англ.]	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

См. также

Примечания

↑ Conway, 2008, с. 288.
↑ Chavey, 1989, с. 147-165.
↑ Uniform Tilings . Дата обращения: 9 сентября 2006. Архивировано из оригинала 9 сентября 2006 года.
↑ Critchlow, 1970, с. 74-75, pattern D.
↑ Conway, 2008.

Литература

Robert Williams. The Geometrical Foundation of Natural Structure: A Source Book of Design. — Dover Publications, Inc., 1979. — С. 37. — ISBN 0-486-23729-X.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
Keith Critchlow. Pattern Q₂, Dual // Order in Space: A design source book. — 1970. — С. 69-61 Pattern G, Dual 77-76, pattern 4.
Dale Seymour, Jill Britton. Introduction to Tessellations. — 1989. — С. 50–56. — ISBN 978-0866514613.
Chavey D. Tilings by Regular Polygons—II: A Catalog of Tilings // Computers & Mathematics with Applications. — 1989. — Т. 17. — doi:10.1016/0898-1221(89)90156-9.

Ссылки

Weisstein, Eric W. Uniform tessellation (англ.) на сайте Wolfram MathWorld.
Weisstein, Eric W. Semiregular tessellation (англ.) на сайте Wolfram MathWorld.
Klitzing, Richard. Euclidean tilings|elong( x3o6o ) - othat - O9

[_632b4181e9930202-1] Conway, 2008, с. 288.

[_54b2d76a459d5cb7-2] Chavey, 1989, с. 147-165.

[uwgb-3] Uniform Tilings . Дата обращения: 9 сентября 2006. Архивировано из оригинала 9 сентября 2006 года.

[_5ca408c85cdb31c7-4] Critchlow, 1970, с. 74-75, pattern D.

[_9a97cef1a655e390-5] Conway, 2008.

[1]

[2]

[3]

[4]

[5]

Усечённая треугольно-шестиугольная мозаика

Содержание

Имена

Однородная раскраскаs

Свазанные 2-однородные мозаики

Упаковка кругов