Усечённая треугольно-восьмиугольная мозаика
| Усечённая треугольно-восьмиугольная мозаика | |
|---|---|
| |
| Тип | Однородная гиперболическая мозаика |
| Конфигурация вершины | 4.6.16 |
| Символ Шлефли | tr{8,3} или |
| Символ Витхоффа | 2 8 3 | |
| Симметрии | [8,3], (*832) |
| Диаграммы Коксетера — Дынкина |    или  
|
| Двойственная мозаика | разделенная ромбическая мозаика порядка 3-8[англ.] |
| Свойства | изогональная |
Усечённая треугольно-восьмиугольная мозаика — это полуправильное замощение гиперболической плоскости. В каждой вершине мозаики имеется один квадрат, один шестиугольник и один шестнадцатиугольник. Символ Шлефли мозаики — tr{8,3}.
Симметрия
[править | править код]
Двойственная мозаика для этой мозаики — кисромбическая мозаика порядка 3-8, и она представляет фундаментальную область симметрии [8,3] (*832). Существует 3 подгруппы малого индекса, строящиеся из [8,3] путём удаления зеркала и альтернацией. В рисунках фундаментальные области раскрашены чередующимся образом, а зеркала находятся на границах между цветами.
Подгруппа с индексом 6, построенная как [8,3*], становится [(4,4,4)], (*444). Подгруппа с индексом 3 строится как [8,3⅄] с удаление 2/3 голубых зеркал.
| Индекс | 1 | 2 | 3 | 6 | |
|---|---|---|---|---|---|
| Диаграммы |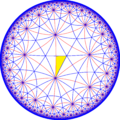 
|
|
|
|
|
| Коксетер (орбифолд) |
[8,3] =   (*832) |
[1+,8,3] =  =    (*433) |
[8,3+] =  (3*4) |
[8,3⅄] =  =  (*842) |
[8,3*] =   =   (*444) |
| Прямые подгруппы | |||||
| Index | 2 | 4 | 6 | 12 | |
| Диаграммы | 
|
|
|
| |
| Коксетер (орбифолд) |
[8,3]+ = (832) |
[8,3+]+ = =  (433) |
[8,3⅄]+ = = (842) |
[8,3*]+ = = (444) | |
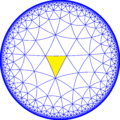
Кисромбическая мозаика порядка 3-8
[править | править код]| Кисромбическая мозаика порядка 3-8 | |
|---|---|
| |
| Тип | Двойственная полурегулярная гиперболическая мозаика |
| Конфигурация грани | V4.6.16 |
| Грани | Прямоугольный треугольник |
| Симметрии | [8,3], (*832) |
| Группа вращения | [8,3]+, (832) |
| Диаграммы Коксетера — Дынкина | 
|
| Двойственная мозаика | Усечённая треугольно-восьмиугольная мозаика |
| Свойства | гранетранзитивная |
Кисромбическая мозаика порядка 3-8 — это полуправильная двойственная мозаика на гиперболической плоскости. Она состоит из конгруэнтных прямоугольных треугольников с 4, 6 и 16 треугольниками в вершинах.
Изображение показывает проекцию гиперболической плоскости на дисковую модель Пуанкаре.
Мозаика обозначается V4.6.16, поскольку каждая треугольная грань (прямоугольный треугольник) имеет три типа вершин — одна с 4 треугольниками, одна с 6 треугольниками и одна с 16 треугольниками. Мозаика является двойственной мозаикой[англ.] для усечённой треугольно-восьмиугольной мозаики, которая имеет в каждой вершине один квадрат, один шестиугольник и один шестнадцатиугольник..
Название
[править | править код]Альтернативным названием является 3-8 kisrhombille (3-8 кисромбический паркет), данное Конвеем. Конвей рассматривал данное замощение как 3-8 ромбическую мозаику, разделённую оператором kis, который добавляет центральную точку в каждый ромб и делит его на четыре треугольника.
Связанные многогранники и замощения
[править | править код]Эта мозаика является одной из 10 однородных мозаик, построенных из гиперболической симметрии [8,3] и трёх подсимметрий [1+,8,3], [8,3+] и [8,3]+.
| Однородные восьмиугольные/треугольные мозаики | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [8,3], (*832) | [8,3]+ (832) |
[1+,8,3] (*443) |
[8,3+] (3*4) | ||||||||||
| {8,3} | t{8,3} | r{8,3} | t{3,8} | {3,8} | rr{8,3} s2{3,8} |
tr{8,3} | sr{8,3} | h{8,3} | h2{8,3} | s{3,8} | |||
|
|
|
|
|
|
|
|
| |||||
|
|
|
  или 
|
или
|
| ||||||||
|
|
 
|
 
|
|
|
|
|
 
|
|
 
| |||
| Однородные двойственные | |||||||||||||
| V83 | V3.16.16 | V3.8.3.8 | V6.6.8 | V38 | V3.4.8.4 | V4.6.16 | V34.8 | V(3.4)3 | V8.6.6 | V35.4 | |||
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
| ||||
Эта мозаика может считаться членом последовательности однородных объектов с вершинной фигурой (4.6.2p)
и диаграммой Коксетера — Дынкина 
.
Для p < 6 членами последовательности являются всеусечёнными[англ.]
многогранники (зоноэдры), показанные ниже как сферические мозаики.
Для p > 6 членам последоавательности являются замощения гиперболической плоскости, начиная с
усечённой треугольно-семиугольной мозаики.
| Симметрия *n32[англ.] n,3[англ.] |
Сферическая | Евклидова | Компактная гиперболическая | Паракомп. | Некомпактная гиперболическая | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Фигуры | 
|
|
|
|
|
|
|
|
|
|
|
|
| Конфигурация | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Двойственная | 
|
|
|
|
|
|
|
|
|
|
|
|
| Конфигурация грани | V4.6.4[англ.] | V4.6.6 | V4.6.8[англ.] | V4.6.10 | V4.6.12[англ.] | V4.6.14[англ.] | V4.6.16[англ.] | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
Смотрите также
[править | править код]- Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
- Разделенная ромбическая мозаика
- Список однородных мозаик на евклидовой плоскости
- Однородные мозаики на гиперболической плоскости
Примечания
[править | править код]Литература
[править | править код]- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 19, The Hyperbolic Archimedean Tessellations // The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
- H. S. M. Coxeter. Chapter 10: Regular honeycombs in hyperbolic space // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 0-486-40919-8.
Ссылки
[править | править код]- Weisstein, Eric W. Hyperbolic tiling (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Poincaré hyperbolic disk (англ.) на сайте Wolfram MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
