Треугольно-семиугольная мозаика

Треугольно-семиугольная мозаика'
Тип	Однородная гиперболическая мозаика
Конфигурация вершины	(3.7)2
Символ Шлефли	r{7,3} или $t{\begin{Bmatrix}7\\3\end{Bmatrix}}$
Символ Витхоффа	2 8 3 |
Симметрии	[8,3], (*832)
Диаграммы Коксетера — Дынкина	или
Двойственная мозаика	Ромбическая мозаика порядка 7-3
Свойства	вершиннотранзитивная, рёбернотранзитивная

Треугольно-семиугольная мозаика — это полуправильное замощение гиперболической плоскости, которое представляет собой полноусеченную семиугольную мозаику. В каждой вершине мозаики имеется два треугольника и два семиугольника. Символ Шлефли мозаики — r{7,3}.

Сравните с треугольно-шестиугольной мозаикой, имеющей конфигурацию вершины 3.6.3.6.

Изображения

модель Клейна этой мозаики представляется прямыми линиями, но углы искажаются

Двойственная мозаика называется ромбической мозаикой порядка 7-3 и состоит из ромбических граней, по 3 и 7 граней в вершинах.

Ромбическая мозаика порядка 7-3

Ромбическая мозаика порядка 7-3
Диаграммы Коксетера — Дынкина
Группа орнамента	[7,3], *732
Группа вращений	[7,3]+, (732)
Конфигурация грани	V3.7.3.7
Двйственная мозаика	Треугольно-семиугольная мозаика
Свойства	рёбернотранзитивная, гранетранзитивная

Ромбическая мозаика порядка 7-3 — это замощение идентичными ромбами на гиперболической плоскости. В мозаике два класса вершин — с тремя и семью ромбами.

Ромбическая мозаика порядка 7-3 в ленточной модели.

Связанные многогранники и замощения

Треугольно-семиугольную мозаику можно видеть в последовательности квазиправильных многогранников и мозаик:

*n32 орбифолдные симметрии квазирегулярных мозаик: (3.n)2
Сим. *n32 [n,3]	Сферическая			Евклидова	Компактная гиперб.		Паракомп.	Некомпактная гиперболическая
	*332 [3,3] Td	*432 [4,3] Oh	*532 [5,3] Ih	*632 [6,3] p6m	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Фигура
Фигура
Вершина	(3.3)2	(3.4)2	(3.6)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2	(3.12i)2	(3.9i)2	(3.6i)2
Шлефли	r{3,3}	r{4,3}	r{5,3}	r{6,3}	r{7,3}	r{8,3}	r{∞,3}	r{12i,3}	r{9i,3}	r{6i,3}
Коксетер
Двойственные однородные фигуры
Двойств. конф.	V(3.3)2	V(3.4)2	V(3.5)2	V(3.6)2	V(3.7)2	V(3.8)2	V(3.∞)2

Согласно построению Витхоффа имеется восемь гиперболических однородных мозаик, которые могут быть основаны на правильном семиугольном замощении.

Раскрашивая плитки красным на месте исходных гранец, жёлтым на месте исходных вершин и синим вдоль исходных рёбер, получим 8 форм.

Однородные семиугольные/треугольные мозаики
Симметрия: [7,3], (*732)							[7,3]+, (732)
{7,3}	t{7,3}	r{7,3}	2t{7,3}=t{3,7}	2r{7,3}	rr{7,3}	tr{7,3}	sr{7,3}
Однородные двойственные мозаики
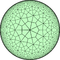
V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14	V3.3.3.3.7

Семейство квазирегулярных многогранников и мозаик: (7.n)2
Симметрия *7n2 [n,7]	Гиперболические...						Паракомпактные	Некомпактные
	*732 [3,7]	*742 [4,7]	*752 [5,7]	*762 [6,7]	*772 [7,7]	*872 [8,7]...	*∞72 [∞,7]	[iπ/λ,7]
Коксетер
Квазирегулярные фигуры конфигурация	3.7.3.7	4.7.4.7	7.5.7.5	7.6.7.6	7.7.7.7	7.8.7.8	7.∞.7.∞	7.∞.7.∞

Смотрите также

• Треугольно-шестиугольная мозаика - 3.6.3.6 мозаика
  • Ромбическая мозаика - двойственная V3.6.3.6 мозаика
• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Список однородных мозаик на евклидовой плоскости