Ромбитришестиугольная мозаика

Ромбитришестиугольная мозаика

Тип	Полуправильная мозаика
Конфигурация вершины	3.4.6.4
Символ Шлефли	rr{6,3} или $r{\begin{Bmatrix}6\\3\end{Bmatrix}}$
Символ Витхоффа	3 \| 6 2
Симметрии	p6, [6,3]⁺, (632)
Диаграммы Коксетера — Дынкина
Акроним Бауэрса	Rothat
Двойственные соты	Дельтоидальная треугольно-шестиугольная мозаика
Свойства	изогональная

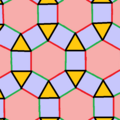
Ромбитришестиугольная мозаика — это полуправильная мозаика на евклидовой плоскости. Мозаика имеет один треугольник, два квадрата и один шестиугольник при каждой вершине. Она имеет символ Шлефли rr{3,6}.

Конвей назвал эту мозаику rhombihexadeltille^[1]. Мозаику можно считать скошеной согласно терминологии Нормана Джонсона или растянутой шестиугольной мозаикой согласно названиям геометрических операций Алиции Стотт^[англ.].

Имеется три правильных и восемь полуправильных мозаик на плоскости.

Однородные раскраски

Имеется только одна однородная раскраска у ромбитришестиугольной мозаики. (Цвета по их индексам вокруг вершины (3.4.6.4): 1232.)

При раскраске рёбер имеется форма с половинной симметрией (3*3) (орбифолдная нотация^[англ.]). Шестиугольники можно считать усечёнными треугольниками t{3} с двумя типами рёбер. Эта мозаика имеет диаграмму Коксетера и символ Шлефли s₂{3,6}. Квадраты могут быть превращены в равнобедренные трапеции. В пределе, когда прямоугольники вырождаются в рёбра, получается треугольная мозаика, .

Симметрия	[6,3], (*632)	[6,3⁺], (3*3)
Название	Ромбитришестиугольная	Скошеная курносая треугольная		Курносая треугольная
Изображение	Однородная раскраска граней	Однородная раскраска рёбер	Неоднородная геометрия	Предел
символ Шлефли	rr{3,6}	s₂{3,6}		s{3,6}
Диаграммы Коксетера

Примеры

Из книги «Грамматика орнамента» (1856)	Кенсингтон (игра)^[англ.]	Мозаичный пол, Археологический музей в Севилье^[англ.], Севилья	Храм Дианы в Ниме, Франция	Римская мозаика на полу в Кастель-ди-Гвидо

Связанные мозаики

Существует одна связанная 2-однородная мозаика^[англ.]^*, в которой шестиугольники разбиты на шесть треугольников^[2]^[3]. Ромбитришестиугольная мозаика связана также с усечённой треугольно-шестиугольной мозаикой^?! путём замены некоторых шестиугольников и окружающих квадратов и треугольников двенадцатиугольниками.

1-однородная	2-однородные разбиения
3.4.6.4	3.3.4.3.4 & 3⁶	CH
Двойственные мозаики
3.4.6.4	4.6.12	3

Упаковка кругов

Ромбитришестиугольная мозаика может быть использована для упаковки кругов, если расположить круги одинакового диаметра с центрами в каждой точке. Каждый круг соприкасается с четырьмя другими кругами в упаковке (контактное число)^[4]. Область решётки параллельного переноса (красный ромб) содержит шесть различных окружностей.

Построение Витхоффа

Существует восемь однородных мозаик, которые могут быть получены из правильной шестиугольной мозаики (или двойственной треугольной мозаики).

Если раскрасить плитки, соответствующие исходным граням, в красный цвет, соответствующие исходным вершинам, в жёлтый цвет, а соответствующие исходным рёбрам, в синий цвет, имеется восемь форм, из которых семь топологически различны (усечённая треугольная мозаика топологически идентична шестиугольной мозаике.)

Однородные шестиугольные/треугольные мозаики
Симметрия: [6,3], (*632)							[6,3]⁺ (632)	[6,3⁺] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}


6³	3.12²^[англ.]	(3.6)²	6.6.6	3⁶	3.4.12.4	4.6.12^[англ.]	3.3.3.3.6	3.3.3.3.3.3
Двойственные им однородные мозаики

V6³	V3.12²^[англ.]	V(3.6)²	V6³	V3⁶	V3.4.12.4	V.4.6.12^[англ.]	V3⁴.6	V3⁶

Варианты симметрий

Эта мозаика топологически сявляется частью последовательности скошеных многогранников с вершинной фигурой (3.4.n.4), и эта последовательность продолжается как мозаики на гиперболической плоскости. Эти вершинно транзитивные фигуры имеют (*n32) зеркальную симметрию (в орбифолдной нотации^[англ.]).

Варианты симметрии *n42 расширенных мозаик: 3.4.n.4
Симметрия *n32 [n,3]	Сферическая				Евклидова	Компактная гиперболическая		Паракомпактная
Симметрия *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Фигура
Конфигурация	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4^[англ.]	3.4.7.4^[англ.]	3.4.8.4^[англ.]	3.4.∞.4^[англ.]

Дельтоидальная треугольно-шестиугольная мозаика

Дельтоидальная треугольно-шестиугольная мозаика

Тип	Двойственная полуправильной мозаике
Конфигурация вершины	3.4.6.4
Группа орнамента	p6m, [6,3], (*632)
Группы вращений	p6, [6,3]⁺, (632)
Диаграммы Коксетера — Дынкина
Двойственные соты	Ромбитришестиугольная мозаика
Конфигурация граней	V3.4.6.4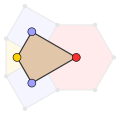
Свойства	гранетранзитивный

Дельтоидальная треугольно-шестиугольная мозаика — это двойственная мозаика полуправильной мозаики, известной как ромбитришестиугольная мозаика. Конвей назвал её tetrille (тетропаркет)^[5]. Рёбра этой мозаики могут быть образованы наложением правильной треугольной мозаики и правильной шестиугольной мозаики. Каждая дельтоидная грань этой мозаики имеет углы 120°, 90°, 60° и 90°. Это одна из восьми мозаик на плоскости, в которых любое ребро лежит на линии симметрии мозаики^[6]

Дельтоидальная треугольно-шестиугольная мозаика является двойственной для полуправильной ромбитришестиугольной мозаики^[7]. Её грани являются дельтоидами.

Связанные многогранники и мозаики

Это одна из семи двойственных однородных мозаик с шестиугольной симметрией, включая правильные двойственные.

Двойственные однородные шестиугольные/треугольные мозаики
Симметрия: [6,3], (*632)						[6,3]⁺, (632)

V6³	V3.12²	V(3.6)²	V3⁶	V3.4.6.4	V.4.6.12	V3⁴.6

Эта мозаика имеет гранетранзитивные варианты, которые могут искажать дельтоиды в равнобедренные трапеции или четырёхугольники более общего вида. Если игнорировать ниже цвета граней, полная симметрия равна p6m, а более низкая симметрия равна p31m с тремя зеркалами в точке и точками тройного вращения^[8].

Гранетранзитивные варианты
Симметрия	p6m, [6,3], (*632)	p31m, [6,3⁺], (3*3)
Форма
Грани	Дельтоид	Половина правильного шестиугольника	Четырёхугольник

Эта мозаика связана с тришестиугольной мозаикой, из которой она может быть получена путём деления треугольников и шестиугольников на треугольники и слиянием соседник треугольников в дельтоиды.

Дельтоидальная треугольно-шестиугольная мозаика является частью множества мозаик, двойственных однородным мозаикам, и является двойственной для ромбитришестиугольной мозаики.

Варианты симметрий

Эта мозаика топологически является частью последовательности мозаик с конфигурацией грани V3.4.n.4, и эта последовательность продолжается в виде мозаик на гиперболической плоскости. Эти гранетранзитивные фигуры имеют (*n32) отражательную симметрию^[англ.].

*n32 варианты симметрии двойственных расширенных мозаик: V3.4.n.4
Симметрия *n32 [n,3]	Сферические				Евклидовы	Компактные гиперболические		Пара- компактные
Симметрия *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Рисунок Конфигурация	V3.4.2.4	V3.4.3.4	V3.4.4.4	V3.4.5.4	V3.4.6.4	V3.4.7.4	V3.4.8.4	V3.4.∞.4

Другие дельтаидальные мозаики

Возможны другие дельтаидальные мозаики.

Точечная симметрия позволяет заполнить плоскость увеличивающимися дельтоидами с топологией квадратного паркета V4.4.4.4 и эта мозаика может быть создана пересекающимися струнами как у ловца снов. Ниже приведён пример с диэдральной шестиугольной симметрией.

Другая гранетранзитивная мозаика с дельтаидальными гранями также является топологическим вариантом квадратной мозаики с конфигурацией грани V4.4.4.4. Мозаика является вершинно транзитивной и каждая вершина содержит все ориентации граней.


Симметрия	D₆, [6], (*66)	pmg, [∞,(2,∞)⁺], (22*)	p6m, [6,3], (*632)
Мозаика
конфигурация	V4.4.4.4		V6.4.3.4

Смотрите также

Примечания

↑ Conway, Burgiel, Goodman-Strauss, 2008, с. 288 table, 288 table.
↑ Chavey, 1989, с. 147-165.
↑ Uniform Tilings (неопр.). Дата обращения: 9 сентября 2006. Архивировано из оригинала 9 сентября 2006 года.
↑ Critchlow, 1970, с. 74-75, pattern B.
↑ Conway, Burgiel, Goodman-Strauss, 2008, с. 288 table.
↑ Kirby, Umble, 2011, с. 283–289.
↑ Weisstein, Eric W. Dual tessellation (англ.) на сайте Wolfram MathWorld. (Смотрите сравнительное наложение этой мозаики и ее двойственной)
↑ Grünbaum, Shephard, 1987.

Литература

Branko Grünbaum, G. C. Shephard. Chapter 2.1: Regular and uniform tilings // Tilings and Patterns. — New York: W. H. Freeman, 1987. — С. 40,58-65. — ISBN 0-7167-1193-1.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
Weisstein, Eric W. Uniform tessellation (англ.) на сайте Wolfram MathWorld.
Weisstein, Eric W. Semiregular tessellation (англ.) на сайте Wolfram MathWorld.
Keith Critchlow. Order in Space: A design source book. — 1970. — С. 69-61, Pattern N, Dual 77-76, pattern 2.
Dale Seymour, Jill Britton. Introduction to Tessellations. — 1989. — С. 50–56. — ISBN 978-0866514613.
Matthew Kirby, Ronald Umble. Edge tessellations and stamp folding puzzles // Mathematics Magazine. — 2011. — Т. 84, вып. 4. — С. 283–289. — doi:10.4169/math.mag.84.4.283. — arXiv:0908.3257.
Chavey D. Tilings by Regular Polygons—II: A Catalog of Tilings. — 1989. — Vol. 17. — doi:10.1016/0898-1221(89)90156-9.
Richard Klitzing. "2D Euclidean tilings x3o6x - rothat - O8".

[_275abaf65b606651-1] Conway, Burgiel, Goodman-Strauss, 2008, с. 288 table, 288 table.

[_54b2d76a459d5cb7-2] Chavey, 1989, с. 147-165.

[uwgb-3] Uniform Tilings (неопр.). Дата обращения: 9 сентября 2006. Архивировано из оригинала 9 сентября 2006 года.

[_5ca408c85cdb31c1-4] Critchlow, 1970, с. 74-75, pattern B.

[_65b416a168eb79c5-5] Conway, Burgiel, Goodman-Strauss, 2008, с. 288 table.

[_558440a2fa9259b4-6] Kirby, Umble, 2011, с. 283–289.

[DT-7] Weisstein, Eric W. Dual tessellation (англ.) на сайте Wolfram MathWorld. (Смотрите сравнительное наложение этой мозаики и ее двойственной)

[_47bc7d67fea083fa-8] Grünbaum, Shephard, 1987.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Ромбитришестиугольная мозаика

Содержание

Однородные раскраски

Примеры